Fisika Kelas Xi Kinematika Dengan Analisis Vektor
-
Upload
ariyani-pratiwi -
Category
Documents
-
view
273 -
download
0
Transcript of Fisika Kelas Xi Kinematika Dengan Analisis Vektor
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
1/45
Drs. Pristiadi Utomo, M.Pd.
FISIKA KELAS XI
Drs. Pristiadi Utomo, M.Pd.
BAB 1KINEMATIKA DENGAN ANALISIS VEKTOR
MOBIL BERGERAK DI JALAN RAYA MEMILIKI KECEPATAN YANGBESARNYA DAPAT DITENTUKAN SEBAGAI KELAJUAN SEDANGKAN
ARAHNYA SELALU BERUBAH-UBAH. SELANG BEBERAPA WAKTULAMANYA MOBIL SUDAH BERUBAH POSISINYA. TERKADANGMOBIL SELAMA PERJALANANNYA HARUS MENAMBAH ATAUMENGURANGI KECEPATANNYA . PERUBAHAN KECEPATAN TIAP
SATUAN WAKTU DINAMAKAN PERCEPATAN. DALAM KINEMATIKAMEMBAHAS POSISI, KECEPATAN, MAUPUN PERCEPATAN SUATUBENDA TANPA MEMPERHATIKAN GAYA-GAYA YANG BEKERJA PADABENDA.
Drs. Pristiadi Utomo, M.Pd. 1
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
2/45
Drs. Pristiadi Utomo, M.Pd.
BAB 1
KINEMATIKA
DENGAN ANALISIS VEKTOR
Drs. Pristiadi Utomo, M.Pd. 2
Kompetensi Dasar
Dapat menganalisis gerak lurus, gerakmelingkar dan gerak parabola denganmenggunakan vektor
Pesawat tempur bergerak di angkasa dengan kecepatan 100 km/jam.Ketika pesawat meluncurkan rudal dengan kecepatan 120 km/jam.Semua kecepatan diukur terhadap tanah. Berarti kecepatan rudal 20km/jam terhadap pesawat. Baik rudal maupun pesawat dikatakanbergerak karena posisinya selalu berubah. amun tidak demikiandengan kendaraan Buldoser yang tengah meratakan tanah namunrodanya tidak pernah bergeser. Buldoser tidak dapat disebut
bergerak pada saat itu karena posisinyaselalu tetap. Buldoserdikatakan bergerak jika sudah bergeser meninggalkan tempat itu.!pakah kamu yang sedang duduk sambil menulis dikatakanbergerak" #arilah kita memperdalam pemahaman tentang gerakatau dalam cabang $isika yang disebut dengan kinematika.
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
3/45
Menganalisis geraklurusmenurutbesaran-besarankinematisnyamenggunakan notasivektor.Menganali
sis gerakparabolamenurutbesaran-besarankinematisnyamenggunakan notasivektor.Menganalisis gerakmelingkarmenurutbesaran-besarankinematisnyamenggunakan notasivektor.
Drs. Pristiadi Utomo, M.Pd.
A. Posisi Ke!epatan dan Per!epatan Partike" pada Gerak L#r#s
Amatilah gerakan mobil balap yang sedangberjalan! Bilakah sebuah mobil dikatakan bergerak
Bagaimana kedudukan mobil terhadap tempat semula
Bagaimana kedudukan mobil terhadap sopirnya
Bagaimana kedudukan sebuah mobil terhadap mobil lain
yang berada di sekitarnya emua permasalahan tersebut
menuntut adanya penjelasan tentang gerak mobil.
"inematika, sebagai #abang dari $isika, mempelajari gerak suatu benda, tanpa
memperhatikan gaya penyebabnya. Dengan demikian berapa kekuatan atau daya yang
dihasilkan oleh mobil tersebut tidak dibahas dalam kajian kali ini. %ada kajian ini hanya
dipelajari tentang kedudukan benda, perubahan kedudukan benda terhadap suatu titik
a#uan, yang sering disebut dengan perpindahan. &uga pada kajian ini dibahas segala
permasalahan gerak yang dikaitkan dengan notasi vektor.
1. Posisi Partike" pada S#at# Bidan$%ada bab ini akan dipelajari tentang vektor posisi, perpindahan, ke#epatan dan
per#epatan dari sebuah partikel, atau benda yang memvisualisasikan sebuah partikel yang
bergerak dua dimensi pada suatu bidang. 'leh karena gerak benda dipandang dalam dua
dimensi, karakterisitiknya akan dianalisis melalui vektor satuan i (sumbu )* dan vektor
satuan j (sumbu y*. +ntuk memahami berbagai hal seperti tersebut di atas, dapat
diilustrasikan seperti berikut ini. uatu ketika ada seorang pelaut sedang berlayar di
tengah laut yang luas. &ika ia berangkat dari kota B menuju kota A, maka langkah
pertama yang dia lakukan adalah menganalisis kedudukan aal dan kedudukan akhirnya.
ebih jelasnya adalah sebagai berikut. Mula-mula pelaut itu berada di kota B. +ntuk
men#apai kota A, ia harus berlayar / km ke utara, dan dilanjutkan 0/ km ke timur, maka
posisi atau kedudukan dari kota A, telah terde$inisikan dengan jelas terhadap kota B
Drs. Pristiadi Utomo, M.Pd. 0
Mobil balap $ormula 1
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
4/45
Drs. Pristiadi Utomo, M.Pd.
sebagai titik a#uan. anpa kerangka a#uan, atau penentuan posisi aal yang dijadikan
a#uan, maka pengertian perpindahan akan sulit dipahami.
aat pilot pesaat terbang akan mendarat di sebuah pelabuhan udara, tentu ia
akan memberi laporan kepada petugas penjaga menara. %ilot akan mengin$ormasikan
kedudukan pesaat tersebut terhadap bandara dan ke#epatan pesaat serta berbagai hal
yang berkaitan dengan persiapan pendaratan. Dengan adanya in$ormasi dari pilot
tersebut, petugas menara akan memberi instruksi teknis tentang pendaratan pesaat.
Dengan demikian, in$ormasi tentang posisi atau kedudukan dari suatu titik, seperti pada
keadaan ilustrasi tersebut, sangat diperlukan.
%ada umumnya, posisi atau kedudukan suatu titik ditunjukkan dengan sebuah
koordinat. ebuah koordinat memiliki suatu titik a#uan, atau suatu kerangka a#uan.
Berdasarkan kerangka a#uan tersebut, akan dapat digambarkan kedudukan suatu titik
dalam koordinat tersebut. Data baha pesaat berada pada jarak 2/ km akan tidak
bermakna, jika tidak disertai arah petunjuk dan titik a#uannya. amun angka 2/ km akan
menjadi in$ormasi penting jika dikatakan, baha pesaat berada 2/ km sebelah timur
dari menara kontrol. Begitu juga dalam koordinat kartesius, yang umumnya
menempatkan koordinat (/,/* sebagai pusat a#uannya. Misalkan dalam koordinat
kartesius titik A berada pada koordinat (2,*, dan titik B pada koordinat (-2,0*.
&ika digambarkan titik (/,/* yang dijadikan sebagai titik a#uan, maka titik A dan B
dapat digambarkan sebagai berikut 3
elain menggunakan gra$ik kartesius, posisi suatu partikel dapat pula ditunjukkan
dengan menggunakan gra$ik koordinat polar (r , 4*. Di mana r adalah jarak suatu titik ke
pusat koordinat, dan 4 adalah sudut dari sumbu ) positi$ dalam koordinat kartesius
menuju titik materi dengan arah berlaanan arah jarum jam. 5ubungan antara koordinat
kartesius dan koordinat polar adalah 3
Drs. Pristiadi Utomo, M.Pd.
6ambar 236ra$ik kartesius yang menggambarkankoordinat A (2,* dan B (-2,0*
6ambar 13%esaat yang akan mendarat selalu melaporkan
posisinya kepada petugas menaraAgar dapat dipandu pendaratannya.%osisi pesaat dikontrol pilot melalui sistem navigasidalam pesaat
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
5/45
Drs. Pristiadi Utomo, M.Pd.
) 7 r . #os 4 y 7 r . sin 4
r7 22 yx + tan 4 7x
y
Misalnya, suatu titik berjarak 1/ #m dari titik pusat koordinat dan membentuksudut 089 terhadap sumbu ) positi$, maka gambaran posisi titik tersebut dalam koordinat
polar adalah seperti berikut ini.
"edudukan dalam koordinat polar dapat diubah dalam koordinat kartesius. Besar
nilai ) dan y adalah 3
) 7 r . #os 4 y 7 r . sin 4
) 7 1/ . #os 089 y 7 1/ . sin 089
) 7 1/ . /,: y 7 1/ . /,;
) 7 : satuan y 7 ; satuan
"edudukan atau posisi suatu benda dinyatakan dalam vektor satuan. Adapunpersamaan umum vektor posisi dalam dua dimensi adalah 3
r 7 ) i< yj di mana besar vektor satuan i7 1
dan besar vektor satuan j7 1
%enulisan suatu vektor satuan dinyatakan dalam %#r#& mirin$.Misalnya vektor
satuan yang searah sumbu ) dinyatakan dengan i. Vektor itu sendiri diakili dengan
%#r#& te'a", seperti vektor kedudukan atau vektor pisisi suatu titik dalam dua dimensiadalah r. %rinsip penulisan lambang seperti tersebut tidak baku namun la=im digunakan
se#ara umum. &ika ingin dibuat suatu teknik penulisan yang lain, dan telah disepakati,
maka hal itu dapat dilakukan, seperti penulisan vektor posisi dengan memberi tanda
panah di atas suatu lambang vektor, atau pemberian harga mutlak pada suatu lambang
vektor untuk melambangkan besar dari suatu vektor.
(onto% )
1. "edudukan suatu t itik D ditunjukkan oleh koordinat kartesius (0,;*. yatakan
koordinat titik tersebut dalam koordinat polar !
&aab 3
r7 22 ;0 + 7 0 > dan tan 4 70
; maka 4 7 ;0,9
Drs. Pristiadi Utomo, M.Pd. >
6ambar 036ra$ik polar yang menunjukkan kedudukan(1/, 089*
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
6/45
Drs. Pristiadi Utomo, M.Pd.
&adi koordinat polarnya (0 > ? ;0,9*
2. "edudukan titik *ditunjukkan oleh koordinat polar (, >9*. yatakan koordinat
tersebut dalam koordinat kartesius !
&aab 3
) 7 r . #os 4 y 7 r . sin 4
) 7 . #os >9 y 7 . sin >9
) 7 . 22
1y 7 . 2
2
1
) 7 2 2 y 7 2 2
0. uatu titik Amempunyai kedudukan yang ditunjukkan koordinat kartesius (2,*.
entukan vektor posisi titik tersebut !
&aab 3rA7 2 i< j
. itik +mempunyai kedudukan (, 0/9*. entukan vektor posisi titik tersebut !
&aab 3
) 7 . #os 4 y 7 r . sin 4
) 7 . #os 0/9 y 7 . sin 0/9
) 7 . 02
1y 7 .
2
1
) 7 2 0 y 7 2
jadi vektor posisinya adalah r+7 2 0 i< 2j
T#$as Indi,id#a"
Buatlah gra$ik perpindahan yang kamu lakukan saat kamu berangkat dari rumah menuju
sekolah! 6unakan skesta dan a#uan arah mata angin. &ika perlu, gunakan kertas milimeter
blok, agar lebih teliti!
-. Perpinda%an
%engertian perpindahan perlu dibedakan dengan jarak. ebagai sebuah ilustrasi,
seandainya ada seorang anak yang berjalan ke timur sejauh1/ m, kemudian kembali ke
arah barat m, maka dikatakan baha perpindahan anak tersebut adalah ; m, namun
jarak yang ditempuhnya sebesar 1 m. Dengan demikian, #oba simpulkan perbedaan
perpindahan dan jarak itu!Adanya perbedaan pengertian perpindahan dan jarak, akan berimplikasi terhadap
pengertian akan ke#epatan (velocity* dan kelajuan (speed*. %erpindahan yang ditempuh
oleh suatu benda tiap satuan aktu akan menunjukkan ke#epatan, dan besarnya jarak
yang ditempuh oleh suatu benda tiap satuan aktu disebut dengan kelajuan.
Drs. Pristiadi Utomo, M.Pd. ;
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
7/45
Drs. Pristiadi Utomo, M.Pd.
uatu benda dikatakan melakukan perpindahan jika posisi dari benda tersebut
mengalami perubahan terhadap titik a#uan. eorang kondektur bus - saat meminta kar#is
penumpang dari baris kursi terdepan menuju kursi belakang - dikatakan telah melakukan
perpindahan. amun seperti yang telah disebutkan sebelumnya, baha perpindahan tidak
sama dengan jarak yang ditempuh. &ika perpindahan sebagai suatu besaran vektor
memperhatikan arah, sedang jarak adalah lintasan total yang dilakukan benda tanpa
memperhatikan arah gerakan benda.
Dalam sistem koordinat kartesius, misalkan suatu titik N, mula-mula saat t 7 /
berada di titik (1,1* m, kemudian saat t 7 s berada pada titik (,>* m, maka besaran-
besaran yang berkaitan dengan vektor perpindahan adalah 3
@ektor posisi aal titik 3r17 1 i< 1j
r27 i< >j
@ektor perpindahan titik 3
r7 r2 r1
r7 ( i< >j* (1 i< 1j*
r7 0 i< j
"omponen vektor perpindahan titik pada sumbu ) adalah 0
"omponen vektor perpindahan titik pada sumbu y adalah
Besar vektor perpindahan titik adalah 3
r= 22 .0 + 7 > m
Arah perpindahan titik adalah 3
tan 4 7x
y
tan 4 70
.
maka 4 7 >0,19 terhadap sumbu ) positi$ dengan arah berlaanan arah jarum jam.
uatu vektor posisi dapat pula dinyatakan dalam sebuah persamaan yang
mengandung unsur t, seperti vektor posisi T 7 >t i < 2 t2j . ehingga misalkan
ditanyakan vektor posisi titik saat t 7 0 s adalah T7 > (0* i< 2 (0*2j 7 1> i< 1:j.
(onto% )
Drs. Pristiadi Utomo, M.Pd. 8
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
8/45
Drs. Pristiadi Utomo, M.Pd.
1. itik Rpada saat t 7 1 s berada pada posisi (2,1* m, dan pada t 7 s pada posisi
(;,* m. entukan 3
a. vektor perpindahannya
b. komponen vektor perpindahan pada sumbu )
#. komponen vektor perpindahan pada sumbu y
d. besar perpindahannya
e. arah perpindahannya
&aab 3
a. rC7 (; i< j* (2 i< 1/* 7 i< 0/
b. rC)7 m
#. rCy7 0 m
d. r722 0. + 7 > m
e. tan 4 7C)
Cy
r
r7.
0 maka 4 7 089
2. itik Imempunyai vektor posisi r7 t 2i< 2 tj. entukan 3
a. @ektor posisi aal (saat t 7 / s*
b. @ektor posisi saat t 7 2 s
#. @ektor posisi saat t 7 s
d. @ektor perpindahan dari t 7 2 s hingga t 7 se. Besar vektor perpindahannya
&aab 3
a. r(t 7 /s*7 / i< /j
b. r(t 72s*7 22i< 2.2j7 i< j
#. r(t7s*7 2i< 2.j7 1; i< :j
d. r7 (1; i< :j* ( i< j* 7 12 i< j
e. r7 22 .12 + 7 1/ m
T#$as Ke"ompok
Buatlah kelompok minimal terdiri atas 0 orang, maksimal > orang. kemudian diskusikan
tentang berbagai perpindahan yang telah kamu lakukan pada hari ini! Apakah dapat
dikatakan baha kamu telah melakukan perpindahan, jika kamu dari kelas pergi ke
belakang, dan kemudian kembali lagi ke kelas
0/i Kompetensi
Drs. Pristiadi Utomo, M.Pd. :
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
9/45
Drs. Pristiadi Utomo, M.Pd.
Ker/akan soa"soa" 'erik#t ini den$an 'enar2
1. 6ambarkan posisi atau kedudukan dari titik-titik berikut ini3
a. 5 (1,* #. (>,>9*
b. A (-0,* d. D (0, ;/9*
2. +bahlah koordinat polar berikut menjadi koordinat kartesius3
a. E (2, 089* #. (0, 0/9*
b. A (;, >09* d. F (, >9*
0. +bahlah koordinat kartesius berikut menjadi koordinat polar3
a. " (0,* d. (1,2*
b. G (-;,-:* e. F (>,->*
#. (:,1/* $. " (-,>*
. itik F melakukan perpindahan dari koordinat (1,* menuju (1,:*. entukan vektorperpindahannya!
>. itik berpindah dari (-1,1* ke (2,>*. entukan3
a. vektor perpindahannya
b. komponen vektor perpindahan pada sumbu )
#. komponen vektor perpindahan pada sumbu y
d. besar vektor perpindahannya
e. arah perpindahannya
;. @ektor posisi dari titik D dinyatakan dalam vektor posisi yang mengandung unsur
aktu, yaitu3 r7 2t i < t2j. entukan3
a. vektor posisi aal
b. vektor posisi saat t 7 1 s
#. vektor posisi saat t 7 2 s
d. vektor perpindahan dari t 7 1 s hingga t 7 2 s
e. komponen vektor perpindahan pada sumbu )
$. vektor perpindahan pada sumbu y
g. besar vektor perpindahan
8. @ektor posisi A dinyatakan dalam r7 (2 < 0t* i < 2t j. entukan besar vektor
perpindahannya dari t 7 2 s hingga t 7 8 s!
:. @ektor posisi 5 dinyatakan dalam r7 t2i 0 j. entukan vektor perpindahan dan
arah perpindahannya dari t 7 1 s hingga t 7 > s!
3. Ke!epatan
Bila suatu partikel mengalami perubahan kedudukan dalam suatu selang aktu
tertentu maka besar perubahan kedudukan dalam selang aktu tesebut disebut kecepatan.
ebagai misal, jika seorang anak pergi ke arah timur sejauh : m dalam sekon, maka
dikatakan ke#epatan anak tersebut 2 mHs. 5al ini akan memiliki makna yang berbeda, jika
Drs. Pristiadi Utomo, M.Pd. I
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
10/45
Drs. Pristiadi Utomo, M.Pd.
dalam sekon berikutnya, anak tersebut kembali ke arah barat : m, maka kedudukan
anak tersebut berada di titik semula, sehingga dapay dikatakan anak tersebut tidak
melakukan perpindahan, sehingga ke#epatannya nol.
a. "e#epatan rata-rata
kecepatan rata-ratadinyatakan sebagai hasil bagi perpindahan terhadap selang
aktu dari perpindahan itu dan dirumuskan3
v 7At
Ar7
12
12
tt
rr
Dengan memperhatikan uraian sebelumnya tentang vektor posisi dari suatu titik,
maka vektor ke#epatan rata-rata dapat ditentukan.
Jontoh3itik materi Dpada detik t 7 1 s berada pada posisi (2,/* m dan pada t 7 s berada pada
posisi (:,:* m. entukan 3
a. vektor ke#epatan rata-ratanya
b. komponen vektor ke#epatan rata-rata pada sumbu )
#. komponen vektor ke#epatan rata-rata pada sumbu y
d. besar vektor ke#epatan rata-rata
e. arah ke#epatan rata-ratanya
&aab 3
a. rD17 2 i< //
rD-7 : i< :/
r7 rD- rD17 ; i< :/ dan t 7 t2 t17 s 1 s 7 0 s
v 7At
Ar70
:; ji +7 ( 2 i< H0/ * mHs
b. )v 7 2 mHs
#. yv 7 H0 mHs
d. v 72
2
0
.2
+ 7 2, mHs
e. tan 4 7)
y
v
v7
( )2
0H.7 /,;;; maka 4 7 00,89
b. "e#epatan esaat
Kecepatan sesaatdide$inisikan sebagai ke#epatan rata-rata untuk selang aktu tyang mendekati nol, yang bila dinyatakan dalam persamaan limit dirumuskan 3
,7 v/t
lim
7
t
)
/t
lim
Drs. Pristiadi Utomo, M.Pd. 1/
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
11/45
Drs. Pristiadi Utomo, M.Pd.
&ika perpindahan suatu titik dilambangkan dalam sumbu ), dan aktu dalam
sumbu y, maka ke#epatan sesaat pada suatu perpindahan ditunjukkan oleh kemiringan
garis singgung pada titik tersebut. %erhatikan gambar berikut!
Dengan gra$ik berikut, tentukan ke#epatan saat t 7 2 s !
+ntuk menentukan ke#epatan sesaat dari suatu gra$ik ) t, yang menunjukkan hubunganantara perpindahan ) terhadap aktu t, maka ke#epatan sesaat ditunjukkan dari
kemiringan garis singgung pada titik yang dimaksud. %ada #ontoh soal di atas,
kemiringan garis singgung pada t 7 2 s digambarkan oleh gra$ik sebagai berikut 3
v 7 tan 4 70
07 1 mHs
&ika dalam suatu penentuan ke#epatan sesaat dari suatu gra$ik bernilai negati$,
berarti arah ke#epatan tersebut berlaanan dengan arah gerakan benda atau arah
perpindahan benda. &uga jika ke#epatan saat itu adalah nol, maka benda dikatakan tidak
berpindah.elain ke#epatan sesaat ditentukan dari kemiringan garis singgung di suatu titik,
ke#epatan sesaat juga dapat diturunkan dari sebuah persamaan perpindahan.
Jontoh3
1. itik *melakukan perpindahan dengan vektor perpindahan 3 r7 ( 2 t 2i< > tj* m.
entukan 3
a. vektor ke#epatan sesaat
b. komponen sumbu ) vektor ke#epatan
#. komponen sumbu y vektor ke#epatan
d. vektor ke#epatan saat t 7 2 s
e. besar ke#epatan saat t 7 2 s
Drs. Pristiadi Utomo, M.Pd. 11
6ambar 36ra$ik ) t yang menjelaskan hubungan antaraperpindahan terhadap aktu, yang digunakan untukmenentukan ke#epatan sesaat
6ambar >3Menganalisis ke#epatan sesaat darikemiringan suatu gra$ik ) - t
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
12/45
Drs. Pristiadi Utomo, M.Pd.
&aab 3
a. , 7dt
dr
,7 ( t i< >j* mHs
b. ,47 t mHs#. ,57 > m
d. aat t 7 2 s , maka vektor ke#epatan sesaat adalah 3 ,7 ( (2* i< >j* mHs
,7 ( : i< >j* mHs
e. ,7 22 >: + 7 :I mHs
&ika vektor ke#epatan sesaat dari suatu titik diketahui, maka vektor perpindahan
dapat ditentukan dari kebalikan turunan, yaitu dengan mengintegralkannya. &adi denganmelakukan integral dari suatu vektor ke#epatan sesaat, maka akan diperoleh vektor posisi
dari suatu titik.
2. itik Amempunyai ke#epatan yang dinyatakan dalam vektor 3
,A7 ( : t i - 2 t2/* mHs
&ika posisi aal benda (2i< 0/* mHs, maka tentukan vektor posisi saat t 7 2 s !
&aab 3
r7 ro< av dt
r7 (2i< 0j* < *2t(:t2ji dt
r7 (2i< 0j* < ( t2i-0
2t0j*
aat t 7 2 s maka r7 (2i< 0j* < ( (2*2i-0
2(2*0j*
r7 ( 1: i-0
8j* mHs
%erbedaan perhitungan perpindahan dan jarak jika diekspresikan dalam sebuah
gra$ik ke#epatan ,terhadap aktu t, ditunjukkan dari luas daerah di baah kurva. &ika
kurva berada di atas sumbu ) atau sumbu t, maka luas tersebut bernilai positi$, namun
jika di baah sumbu ) atau sumbu t, maka luas daerah tersebut bernilai negati$.
0. Fndah melempar benda dengan persamaan ke#epatan v 7 (0t2 12* mHs.entukan
perpindahan dan jarak antara t 7 / hingga t 7 0 s!
&aab 3
angkah pertama adalah menginterpretasikan persamaan v 7 (0t2 12* mHs dalam
sebuah gra$ik.
Drs. Pristiadi Utomo, M.Pd. 12
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
13/45
Drs. Pristiadi Utomo, M.Pd.
%erpindahan 7 luas baah < luas atas
%erpindahan 7 0
/
2 120t dt
%erpindahan 7 [ ]0/
0 12tt
%erpindahan 7 K00 12.0L K/0 12./L
%erpindahan 7 - I m (tanda (-* berarti arah perpindahan berlaanan
dengan arah ke#epatan
&arak 7 - luas baah < luas atas
&arak 7 - 2
/
2 120t dt < 0
2
2 120t dt
&arak 7 - [ ] 2/0 12tt < [ ]0
2
0 12tt
&arak 7 - K20 12.2L K/0 12./LN < K00 12.0L K20 12.2LN
&arak 7 - K: 2L K/ /LN < K28 0;L K: 2LN
&arak 7 - - 1; N < 8 N
&arak 7 20 m
Jontoh : 3
Oitri mengendarai sepeda dengan ke#epatan seperti gra$ik berikut 3
entukan 3
Drs. Pristiadi Utomo, M.Pd. 10
6ambar 3Menginterpretasikan sebuah persamaanke#epatan dalam sebuah gra$ik, dapat dilakukandengan membuat tabel antara t dan v, kemudianmenyusunnya dalam sebuah gambar gra$ik.
6ambar ;36ra$ik hubungan v dan t yangmenggambarkan gerakan sepeda
yang dilakukan Oitri.
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
14/45
Drs. Pristiadi Utomo, M.Pd.
a. &arak yang ditempuh setelah sepeda Oitri bergerak 2 s.
b. &arak total yang ditempuh Oitri selama : s.
&aab 3
a. &arak 7 uas segitiga 7 F
&arak 7 P . alas . tinggi
&arak 7 P . 2 . 7 m
b. &arak 7 F < FF < FFF
&arak 7 ( P . 2 . * < ( . * < ( P . 2 . *
&arak 7 < 1; < 7 2 m
ugas "elompok
6ambarlah ruang kelasmu dalam sebuah kertas milimeter blok dan tunjukkan posisi mejamasing-masing temanmu! elanjutnya, tentukanlah jarak dan perpindahan meja teman-
temanmu dalam satu kelas terhadap meja guru! "umpulkan denah ruang kelasmu pada
guru untuk dinilai. Denah yang terbaik, layak untuk dipasang di dinding.
Drs. Pristiadi Utomo, M.Pd.
Peker/aan R#ma%
Amatilah gerakan gereta api pada lintasan rel keretaapi. Apakah gerakannya beraturan atau berubah
beraturan Apakah posisi yang ditempuh memilikivektor satuanjdan k1.Buatlah persamaan posisi sebagai $ungsi aktudari gerak kereta tersebut!2.Buatlah persamaan ke#epatan $ungsi aktu darikereta tersebut!0. Buatlah persamaan per#epatan $ungsi aktu darikereta tersebut.
6ambar 83 "ereta api yang bergerak
1
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
15/45
Drs. Pristiadi Utomo, M.Pd.
0/i Kompetensi
&aablah soal-soal berikut bersama dengan benar!
1. itik Npada t 7 / berada pada posisi (2,>* m, kemudian pada t 7 2 s berada pada
posisi (2,:* m. entukan besar vektor ke#epatan rata-ratanya!
2. itik Aberada dititik (/,/* saat t 7 / s. &ika pada t 7 s, berada di (0,* maka
tentukan vektor ke#epatan rata-ratanya!
0. itik Rmelakukan gerak dan digambarkan dalam gra$ik hubungan antara
perpindahan ()* dengan aktu (t*. entukan besar ke#epatan saat t 7 > s !
. %artikel 6melakukan perpindahan sesuai vektor perpindahan3
r7 ( 0 t2i< tj* m. entukan3
a. @ektor ke#epatan sebagai $ungsi aktu,
b. Besar vektor ke#epatan saat t 7 2 s.
>. itik Amelakukan gerakan pada arah mendatar dengan vektor ke#epatan
,7 ( t i < 2j* mHs. &ika posisi aal titik berada di posisi 0 m, tentukan
vektor posisi titik saat t 7 2 s!
;. &ika benda Tbergerak pada suatu arah tertentu dengan persamaan ke#epatan
,7 (t2- 2 * mHs. entukan perpindahan dan jarak dari t 7 / s hingga t 7 s !
8. itik materi Pmelakukan gerak sesuai gra$ik berikut.
entukan 3
a. &arak yang ditempuh setelah t 7 2 sb. &arak yang ditempuh setelah t 7 s
#. &arak yang ditempuh setelah t 7 > s
d. &arak yang ditempuh setelah t 7 ; s
e. &arak yang ditempuh setelah t 7 8 s
Drs. Pristiadi Utomo, M.Pd. 1>
6ambar :36ra$ik hubungan perpindahan terhadap aktu.
6ambar I36ra$ik v t dari gerak titikmateri %
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
16/45
Drs. Pristiadi Utomo, M.Pd.
7. Per!epatan
%erubahan ke#epatan tiap satuan aktu disebut dengan per#epatan. ebagai
#ontoh, saat kamu berangkat ke sekolah naik motor, motor yang kamu kendarai tentu
tidak berjalan pada ke#epatan yang tetap. Motor yang kamu naiki kadang bergerak
dengan ke#epatan tinggi, kadang lambat, dan kadang harus berhenti karena terhalang
lampu pengatur lalu lintas.
a. %er#epatan rata-rata
Adapun pengertian per#epatan rata-rata adalah perubahan ke#epatan dalam selang
aktu tertentu. emakin besar perubahan ke#epatan yang dilakukan, maka tentuper#epatan yang dihasilkan semakin besar. Begitu juga jika selang aktu yang digunakan
untuk melakukan perubahan semakin sempit, maka besar per#epatan yang dilakukan
semakin besar. Adapun besar dari per#epatan rata-rata dirumuskan 3
a 7At
Av7
12
12
tt
vv
%enguraian besaran-besaran yang berhubungan dengan per#epatan rata-rata
diperoleh dengan proses yang analogi dengan memperoleh ke#epatan rata-rata seperti
diuraikan pada bagian sebelumnya.
Jontoh 3
1. 5a$id= menaiki motor dengan persamaan ke#epatan ,7 ( 2t2i< : tj* mHs.
entukan3
a. vektor per#epatan rata-rata dari t 7 1 s hingga t 7 0 s
b. komponen sumbu ) per#epatan rata-rata dari t 7 1 s hingga t 7 0 s
#. komponen sumbu y per#epatan rata-rata t 7 1 s hingga t 7 0 s
d. besar per#epatan rata-rata dari t 7 1 s hingga t 7 0 s
e. arah per#epatan rata-rata dari t 7 1 s hingga t 7 0 s
&aab3
a. a 7At
Av7
12
12
tt
vv
a 7*10(
*L1.:1.2(*0.:0.2K( 22
++ jiji 7 ( : i< :j* mHs2
b. )a 7 : mHs2
#. ya 7 : mHs2
d. a 7 22 :: + 7 : 2 mHs2
Drs. Pristiadi Utomo, M.Pd. 1;
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
17/45
Drs. Pristiadi Utomo, M.Pd.
e. tan 4 7:
:maka 4 7 >9
b. %er#epatan sesaat
%er#epatan sebagai perubahan ke#epatan terhadap aktu dapat ditentukan dengananalogi seperti ke#epatan sesaat, maka per#epatan sesaat dapat ditentukan dengan
menentukan kemiringangaris singgung pada kurva v - t.
elain dengan menentukan kemiringan suatu gra$ik v - t, vektor per#epatan dapat
juga ditentukan dengan menurunkan$ungsi v terhadap t. Dengan demikian terdapat dua
#ara yang dapat digunakan dalam menentukan per#epatan sesaat, yaitu melalui
kemiringan gra$ik, atau dengan #ara menurunkan $ungsi dari ke#epatan sesaat.
Jontoh3
1. entukan per#epatan saat t 7 2 s, berdasar gra$ik v - t berikut ini3
&aab3
&ika dianalisis, saat t 7 2 s maka kemiringan garis singgungnya adalah3
a7 tan 4
a71/
I7 /,I mHs2
Drs. Pristiadi Utomo, M.Pd. 18
6ambar 1/36ra$ik v - t untuk menentukanper#epatan rata-rata.
6ambar 113Menganalisis gra$ik v-t untukmenentukan per#epatan rata-rata
melalui kemiringan gra$ik pada suatutitik.
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
18/45
Drs. Pristiadi Utomo, M.Pd.
2. "e#epatan mobil Eatik digambarkan oleh gra$ik berikut3
entukan per#epatan mobil saat3
a. t 7 1 s
b. t 7 > s
#. t 7 8 s&aab3
a. a 7 tan 4 72
.7 2 mHs2 (t 7 1 s bagian kemiringan garis t 7 / sampai t 7
2 s*
b. a 7 tan 4 7.
/7 / mHs2
#. a 7 tan 4 72
.7 - 2 mHs2
0. uQman menaiki motor dengan ke#epatan ,7 (0 t2 ->* mHs
entukan per#epatan motor uQman saat t 7 0 s!
8a9a')
a 7dt
dv
a 7 ; t mHs2
saat t 7 0 s, maka a 7 ; .0 7 1: mHs2
. %er#epatan motor yang dinaiki oval adalah a7 2t i: 0 t2
j&ika ke#epatan aal motor oval adalah nol, tentukan ke#epatan motor oval
saat
t 7 2 s!
8a9a' )
,7 ,o< (2t i: 0 t2j* dt
,7 / < t2i: t0j
aat t 7 2 s maka ,7 22i< 20j7 i< :j
0. uatu titik =at bergerak dengan per#epatan $ungsi dari aktu yaitu a 7 t 2, dan
dengan ke#epatan aal vo7 1/ mHs. ernyata pada suatu saat ke#epatannya ialah v 7
>/ mHs. Berapa lama titik =at bergerak
to7 / R @o7 1/ mHs
Drs. Pristiadi Utomo, M.Pd. 1:
6ambar 1236ra$ik hubungan v - t untuk
menetukan per#epatan sesaat.
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
19/45
Drs. Pristiadi Utomo, M.Pd.
t 7 S R @ 7 >/ mHs
a 7 t 2
dv 7 a dt
]//22/
221/>/
*2(
2
2
/
=
=
=
=
tt
tt
dttVV
dtdv
t
o
t
to
t
to
v
Vo
. uatu titik =at bergerak pada sumbu ) se#ara 6BB dengan per#epatan >mHs2. %ada
saat bergerak 2 sekon ke#epatannya 2/ mHs. Mulai berangkat kedudukannya di ) 7
-1>m. entukan persamaan posisi titik =at tersebut.
1/>tv
1/#
#>.22/
mHs2/v2t
#>tv
>tv
adtdv
adtdv
+=
=
+=
==
+=
=
=
=
1/>tv
1/#
#>.22/
mHs2/v2t
/1t2
>)
*1/(>t)
dtvd)
dtvd)
2
+=
=
+=
==
+=
+=
=
=
dt
%ersamaan posisi 3
>. ebuah partikel bergerak lurus dengan per#epatan a 7 12-0s dengan a dalam mHs2dan
s dalam m.
Jari hubungan antara ke#epatan dan perpindahan jika s 7 2 m, v 7 mHs
2/0s2sv
2/0s2sv
1/s2
012sv2
1
1/#
#;2:
#22
012.2.
2
1
v2s
s2
012sv
2
1
0s*ds(12sv2
1
adsvdv
2
2
22
22
22
2
=
=
=
=
+=
+=
==
=
=
=
Drs. Pristiadi Utomo, M.Pd. 1I
(M*(M*
.dett>det,t
/.t@/>t
/.*(t>*(t/2/tt
/./2t2t
2
2
==
=+=
=+=
=
1>*i1/tt2
>(r 2 ++=
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
20/45
Drs. Pristiadi Utomo, M.Pd.
&ika dalam permasalahan yang ditemui adalah penentuan ke#epatan dari gra$ik a t atau
penentuan ke#epatan dari $ungsi per#epatan, maka ke#epatan suatu titik, dapat ditentukan
dari integral $ungsi dari per#epatan tersebut. e#ara matematis, $ungsi integral tersebut
senilai dengan luas daerah di baah gra$ik. Dengan demikian, jika kita mengetahui luas
daerah dibaah gra$ik per#epatan terhadap aktu maka nilai ke#epatan sesaat dapat
ditentukan.
%ersamaan vektor ke#epatan dapat ditentukan dengan mengintralkan persamaan vektor
per#epatan, sehingga persamaan vektor ke#epatan
v 7 vT i < v j R vT 7 ,/T< aT dt v 7 ,/< a dt
(onto%)
1. ebuah mobil bergerak dengan ke#epatan v 7 ( t2
->t* mHs entukan per#epatan mobil saat t 7 s !
8a9a' )
a 7dt
dv
a 7 2t - > mHs2 7 2. > 7 0 mHs2
jadi a 7 0 mHs2
2. %er#epatan yang dimiliki mobil eko dalah a7 t 0i : 0 t2/
&ika ke#epatan aal adalah 2i, tentukan vektor ke#epatan mobil tersebut dan
besarnya ke#epatan ketika t 7 s !
8a9a' )
,7 ,o< ( t 0i : 0 t2/ * dt
,7 2 i . Buat perbandingan kesimpulan dari kedua aktu tibanya kedua bola di tanah!
;. Analisislah gerakan kedua bola tersebut!
Beberapa asumsi penyederhanaan yang digunakan dalam membahas gerak paraboladalam kajian ini adalah baha hambatan udara dan rotasi bumi tidak mempengaruhi
dalam perhitungan, dan nilai pe#epatan gravitasi bumi dianggap 1/ mHs2, ke#uali terdapat
penjelasan dalam soal.
Drs. Pristiadi Utomo, M.Pd. 2>
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
26/45
Drs. Pristiadi Utomo, M.Pd.
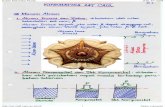
6ambar 1;3 6ra$ik lintasan parabola.
Beberapa persamaan yang berhubungan dengan gerak parabola adalah 3umbu T 3
vo) 7 vo. #os 4
v) 7 vo. #os 4
) 7 v). t 7 vo. #os 4 . t
umbu 3
voy 7 vo. sin 4
vy 7 vo. sin 4 g . t
y 7 vo. sin 4 . t P . g . t 2
%ersamaan ke#epatan dan arah gerakan partikel 3
v 7 02 yx vv +
tan X 7x
y
v
v
"eterangan 3
1. vo 7 ke#epatan aal (mHs*
2. vo) 7 ke#epatan aal pada sumbu ) (mHs*
0. voy 7 ke#epatan aal pada sumbu y (mHs*
. v) 7 ke#epatan pada sumbu ) (mHs*
>. vy 7 ke#epatan pada sumbu y (mHs*
;. v 7 ke#epatan pada suatu saat (mHs*
8. ) 7 kedudukan atau posisi pada sumbu ) (m*
:. y 7 kedudukan atau posisi pada sumbu y (m*I. X 7 arah gerakan partikel (9*
1/. 4 7 sudut elevasi (9*
11. g 7 per#epatan gravitasi bumi (mHs2*
Drs. Pristiadi Utomo, M.Pd. 2;
6ambar 183 berbagai posisi pada lintasan gerak parabola
=
5
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
27/45
Drs. Pristiadi Utomo, M.Pd.
Beberapa hal penting berkaitan dengan gerak parabola31. %ersamaan yang tersebut pada bagian aal didasarkan pada gerakan benda yang
mengarah ke atas, sedang arah per#epatan gravitasi bumi ke baah, sehingga
persamaan di atas menggunakan tanda negati$ (-* untuk nilai g. amun jika
gerakan diaali dengan gerak ke baah, seperti gerakan bom yang dijatuhkan dari
pesaat, maka arah gerak benda searah dengan per#epatan gravitasi, sehingga
persamaan yang mengandung unsur g yang semula negati$, berubah menjadi positi$,
karena arah gerak benda searah dengan arah per#epatan benda.
2. %ada titik tertinggi nilai vy7 / mHs, sehingga nilai v 7 vo)7 v)
0. %ada titik terjauh nilai y 7 /. &ika saat men#ari t dari y 7 /, diperoleh dua nilai t, di
mana salah satu nilainya umumnya nol, maka nilai t yang digunakan adalah yang
besar.
Disk#si Ke"ompok
Buatlah kelompok maksimum > orang untuk berdiskusi se#ara matematis dan
membuktikan persamaan matematis berikut ini 3
a. "oordinat titik pun#ak ()MAT, y MAT*
dimana )MAT7g
v
2
2sin2
/ , y MAT7g
v
2
sin22
/ , X 7 sudut elevasi
g 7 per#epatan gravitasi bumi (mHs2*
vo7 ke#epatan aal (mHs*
b. Eaktu untuk men#apai titik tertinggi atau tinggi maksimum t%7g
v sin/
Eaktu untuk men#apai jarak mendatar terjauh atau jatuh kembali ke tanah t&7 2. t%
#. &arak mendatar terjauh ) &auh7 2 )MAT
Drs. Pristiadi Utomo, M.Pd. 28
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
28/45
Drs. Pristiadi Utomo, M.Pd.
&arak mendatar men#apai maksimum ketika sudut elevasi X 7 >/
d. %asangan sudut elevasi (X1dan X2 * akan men#apai jarak mendatar terjauh yang
sama jika
X1< X2 7 I//
(onto% )
1. ebuah panah dilepaskan dari busur dengan ke#epatan aal 1// mHs dan sudut
elevasi 089 entukan 3
a. vektor posisi panah saat t 7 1 s
b. vektor posisi ketika panah men#apai titik tertinggi.
#. vektor posisi di titik mendatar terjauh
d. vektor ke#epatan dan besarnya saat t 7 1 s
e. arah ke#epatan saat t 7 1 s
8a9a' )
a. ) 7 vo. #os 4 . t 7 1// . #os 089 . 1 7 1// . /,: 7 :/ m
y 7 vo. sin 4 . t P g t 2 7 1// . sin 089 . 1 P .1/.127 (1// ./,; >* 7 >> m
&adi vektor posisi panah setelah 1 s adalah r 7 (:/ i < >> j* mb. %ada titik tertinggi vy7 / sehingga 3
vy 7 vo sin 4 g . t
/ 7 1// . sin 089 1/ . t maka diperoleh nilai t
t 7 ; s
ilai t tersebut kemudian dimasukkan pada
) 7 vo. #os 4 . t 7 1// . #os 089 .; 7 1// . /,: . ; 7 :/ m
y 7 vo. sin 4 . t P . g . t 2 7 1// . sin 089 ; P .1/. (;*27 0;/ 1:/ 71:/ m
&adi vektor posisi panah pada titik tertinggi adalah r 7 (:/ i < 1:/ j* m
#. %ada titik mendatar terjauh y 7 /, kemudian nilai t tersebut dimasukkan ke )
y 7 vo. sin 4 . t P . g . t 2
/ 7 1// . sin 089 . t P .1/. t2 R / 7 ;/ t > t2
- ;/ t 7 - > t2 R t 7 12 sekon
maka ) 7 vo. #os 4 . t 7 1// . #os 089 .12 7 82/ m
&adi vektor posisi panah di titik mendatar terjauh adalah r 7 (82/ i < / j* m
d. v) 7 vo. #os 4 7 1// . #os 089 7 1// . /,: 7 :/ mHs
vy 7 vo. sin 4 g . t 7 1// sin 089 1/ . 1 7 (;/ - 1/* 7 >/ mHs
jadi vektor ke#epatan panah v 7 vT i < v j 7 :/ i < >/ j
Besarnya v 7 02 yx vv + 7 ( ) ( )22 >/:/ + 7 2>//;// + 7 I,00 mHs
Drs. Pristiadi Utomo, M.Pd. 2:
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
29/45
Drs. Pristiadi Utomo, M.Pd.
e. tan 4 7x
y
v
v 7
:/
>/7 /,;2> maka 4 7 029
2. "etika terjadi ben#ana sunami, banyak daerah yang membutuhkan bantuan
makanan dan alat-alat kesehatan, akan tetapi lokasi bantuan sulit terjangkau. +ntuk
mengatasinya bahan makanan dan bantuan alat kesehatan tersebut dijatuhkan dari
pesaat militer. &ika bantuan makanan dijatuhkan pada ketinggian >// dari pesaat
pengangkut yang bergerak mendatar dengan ke#epatan >/ mHs, maka hitunglah
jarak mendatar dari pesaat ke lokasi agar bantuan makanan jatuh tepat pada
sasaran
&aab 3
) 7 .... y/ 7 >// m y 7 / 4 7 / /
y 7 y/ < vo. sin 4 . t < P . g . t 2
/ 7 >// < / - P . 1/ . t 2 maka t 7 1/ s
) 7 vo). t 7 vo. #os 4 . 1/ . 7 >/ . 1 .1/ 7 >// m
0. ebuah bola ditendang dengan sudut elevasi >9 dan ke#epatan aal 2/ mHs.
entukan3
a. posisi saat t 7 1 s
b. koordinat titik tertinggi
#. koordinat titik terjauh
d. ke#epatan saat t 7 1 s
e. arah ke#epatan saat t 7 1 s
8a9a' )
a. ) 7 vo. #os 4 . t 7 2/ . #os >9 . 1 7 1/ 2 mHs
y 7 vo. sin 4 . t P . g . t 2 7 2/ . sin >9 . 1 P .1/.127 (1/ 2 >* mHs
&adi posisi bola setelah 1 s adalah (1/ 2 ? 1/ 2 >* mHs
b. %ada titik tertinggi vy7 / sehingga 3
vy 7 vo. sin 4 g . t
/ 7 2/ . sin >9 1/ . t maka diperoleh nilai t
t 7 2 s
ilai t tersebut kemudian dimasukkan pada3
) 7 vo. #os 4 . t 7 2/ . #os >9 . 2 7 2/ mHs
y 7 vo. sin 4 . t P . g . t 2 7 2/.sin >9 . 2 P .1/. ( 2 *2 7 1/ mHs
&adi posisi bola pada titik tertinggi adalah (2/, 1/* mHs.
#. %ada titik terjauh y 7 /, kemudian nilai t tersebut dimasukkan ke )y 7 vo. sin 4 . t P . g . t 2
/ 7 2/ . sin >9 . t P .1/. t2
maka diperoleh nilai t 7 / atau t 7 2 2 s. 6unakan t 7 2 2 s maka
) 7 vo. #os 4 . t 7 2/ . #os >9 . 2. 2 7 / m
Drs. Pristiadi Utomo, M.Pd. 2I
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
30/45
Drs. Pristiadi Utomo, M.Pd.
&adi posisi bola di titik terjauh adalah (/ , /* m
d. v) 7 vo. #os 4 7 2/ . #os >9 7 1/ 2 mHs
vy 7 vo. sin 4 g . t 7 2/ . sin >9 1/ . 1 7 (1/ 2 - 1/* mHs
v 7 02 yx vv + 7 ( ) ( )22
1/21/21/ + 7 1/ 22> mHs
e. tan X 7x
y
v
v 7
21/
*1/21/( 7 /,2I0 maka X 7 1;,09
. Dari pun#ak gedung setinggi 12> m, Arsa melempar bola mendatar dengan
ke#epatan 1/ mHs. entukan 3
a. aktu yang diperlukan bola untuk men#apai tanah
b. jarak mendatar yang ditempuh bola
8a9a' )
a. vo) 7 1/ mHs dan voy 7 / mHs
y 7 vo. sin 4 . t < P . g . t 2
12> 7 / < P . 1/ . t 2 maka t 7 > s
b. ) 7 vo). t 7 1/ . > 7 >/ m
0/i Kompetensi
1. ebuah anak panah dilepaskan dari busur dengan ke#epatan aal >/ mHs dan sudut
elevasi ;/9. entukan vektor posisi ketika anak panah menyentuh tanah.2. &ika sebuah rudal kendali dijatuhkan dari pesaat pada ketinggian 1/// m di atas
permukaan tanah, dengan ke#epatan mendatar 1// mHs, maka tentukan jarak
mendatar yang ditempuh rudal kendali.
0. ebuah bola ditendang dengan ke#epatan aal >/ mHs dengan sudut elevasi >09
membentuk lintasan gerak parabola dengan per#epatan gravitasi bumi g 71/ mHs.
entukan 3
a. vektor posisi bola ketika t 7 2 sekon.
b. vektor posisi dan ke#epatan bola ketika men#apai titik tertinggi.
#. vektor ke#epatan dan besar ke#epatan bola saat t 7 sekon.
d. arah ke#epatan bola ketika t 7 sekon.e. vektor posisi bola ketika men#apai tanah.$. aktu untuk men#apai tanah.
. Anggun melemparkan bola basket dengan vektor posisi r 7 2 t i < ( t2 -2*/.
entukan vektor posisi dan vektor ke#epatan ketika bola men#apai tertinggi.
Drs. Pristiadi Utomo, M.Pd. 0/
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
31/45
Drs. Pristiadi Utomo, M.Pd.
>. %erhatikan gambar di baah. ebuah anak panah dilepaskan dengan vektor
ke#epatan vektor v 7 2 i < :t j maka tentukan vektor posisi sebagai $ungsi aktu
dan vektor ke#epatan panah ketika tiba ditanah.
Ke$iatan Ke"ompok
Bentuklah sebuah kelompok yang beranggotakan 0 > orang!
Diskusikan dalam kelompokmu tentang beberapa jenis gerak yang ada di sekitar kita
yang termasuk gerak parabola! Apakah gerakan pesaat terbang saat naik termasukgerak parabola Apakah gerak bom atom saat dijatuhkan dari pesaat pengebom di
5irosima termasuk gerak parabola Apakah gerakan roket Gksoset saat diarahkan ke
pesaat tempur merupakan gerak parabola Apakah gerak peluru yang ditembakkan
ke atas merupakan gerak parabola
Peker/aan R#ma%
1. anti memukul shuttle cockdengan ke#epatan aal 2/ mHs dan sudut elevasi ;/9.
entukan jarak terjauh yang ditempuh shuttle #o#k tersebut !
2. ebuah bom dijatuhkan dari pesaat di ketinggian 2./// m di atas permukaan
tanah, dengan ke#epatan mendatar 2// mHs. entukan jarak mendatar yang
ditempuh bom!
0. ebuah bola ditendang dengan ke#epatan aal 1/ mHs sehingga mengenai dinding
setinggi 2/ m dan jarak mendatar / m. entukan sudut elevasinya !. "opral &ono menembakkan peluru dengan sudut elevasi >9 dan ke#epatan aal
1// mHs. entukan koordinat titik tertingginya!
>. Dimas melempar bola dengan vektor posisi r7 > t i< (2 t2-1*j, tentukan vektor
posisi titik tertinggi yang di#apai bola.
Drs. Pristiadi Utomo, M.Pd. 01
6ambar 1:3 Anak panah dilepaskan membentuk lintasan parabola.
1,> m
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
32/45
Drs. Pristiadi Utomo, M.Pd.
;. ouval melempar batu dengan vektor posisi r7 2 t2i< ( t2- :t*j. entukan vektor
posisi pada jarak terjauhnya!
(. Posisi S#d#t Ke!epatan S#d#t dan Per!epatan S#d#t pada Gerak Me"in$kar
1. Posisi S#d#t
%osisi sudut akan menggambarkan kedudukan dari suatu sudut dalam gerak
melingkar beraturan. entu saja pusat gerak melingkar tersebut akan dijadikan sebagai
pusat titik a#uan. eperti telah disampaikan terdahulu, baha semua gerak tetap
memerlukan suatu titik a#uan.
Besarnya sudut yang ditempuh gerak melingkar tersebut tiap satuan aktu disebut
dengan ke#epatan sudut. Dalam hal ini, satuan dari ke#epatan sudut dapat dinyatakandalam radHs atau putaran per menit (rpm*. %erubahan kedua satuan tersebut didasarkan
baha satu putaran senilai dengan 2 Y radian.
edangkan per#epatan sudut adalah laju perubahan ke#epatan sudut yang terjadi
tiap satuan aktu. emakin besar perubahan ke#epatan sudut yang terjadi, maka akan
semakin besar pula ke#epatan sudut yang terjadi pada gerak melingkar tersebut.
Demikian juga jika semakin besar pengurangan ke#epatan sudut yang dilakukan gerak
melingkar maka semakin besar nilai perlambatan sudut dari gerak melingkar itu.
-. Ke!epatan S#d#t
&ika kita memperhatikan seorang pesenam di atas lantai es yang li#in saat ia
melakukan gerak melingkar, maka gerakan tubuhnya yang semula bergerak melingkar
beraturan akan berubah menjadi bergerak melingkar berubah beraturan semakin #epat
saat ia mengubah posisi dari tangannya, serta memberikan sejumlah gaya pada dirinya.
a. Ke!epatan s#d#t ratarata
"e#epatan sudut rata-rata sebagai hasil bagi perpindahan sudut dengan selang
aktu yang ditempuh dapat dirumuskan3
7t
'. Ke!epatan s#d#t sesaat
edang ke#epatan sudut sesaat adalah turunan pertama dari posisi sudut, atau dapat
pula ditentukan dari kemiringan garis singgung gra$ik posisi sudut terhadap aktu.
"e#epatan sudut sesaat dirumuskan3
dt
d=
3. Per!epatan S#d#t
Drs. Pristiadi Utomo, M.Pd. 02
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
33/45
Drs. Pristiadi Utomo, M.Pd.
a. Per!epatan s#d#t ratarata
%er#epatan sudut rata-rata adalah hasil bagi ke#epatan sudut dengan selang aktu
yang ditempuh. %er#epatan sudut rata-rata dirumuskan3
7t
'. Per!epatan s#d#t sesaat
%er#epatan sudut sesaat adalah turunan pertama dari ke#epatan sudut, atau dapat
pula ditentukan dari kemiringan garis singgung gra$ik ke#epatan sudut terhadap aktu.
%er#epatan sudut sesaat dirumuskan3
dt
d=
Joba kamu amati gerak roda motor dalam perjalanan menuju ke sekolah! elama
perjalanan roda tersebut tidak mungkin memiliki ke#epatan sudut yang tetap. Coda itu
kadang berputar pelan, karena harus menghindari rintangan, atau kadang harus berputar
lebih #epat karena meleati jalan lurus dan sepi tanpa hambatan. Bahkan roda itu kadang
harus berhenti karena lampu merah pengatur jalan raya menyala. Adanya perubahan
ke#epatan sudut dari roda tersebut akan menunjukkan besar dari per#epatan sudut yang
terjadi pada roda.
(onto% )
1. %osisi sebuah sudut ditentukan oleh persamaan 3
4 7 (0 t2< 2* rad, maka tentukan 3
a. posisi sudut saat t 7 / s
b. posisi sudut saat t 7 2 s
#. ke#epatan sudut rata-rata dari t 7 / s hingga t 7 2 s
d. ke#epatan sudut saat t 7 0 s
8a9a' )
a. 4 7 (0 (/*2< 2* 7 2 rad
b. 4 7 (0 (2*2< 2* 7 1 rad
#. 7t
7
*/2(
*21(
7 ; radHs
d. Z 7dt
d7 (; t * 7 ( ; . 2 * 7 12 radHs
2. %osisi sebuah sudut ditentukan oleh persamaan3
4 7 (2 t2< >* rad, maka tentukan 3
a. posisi sudut saat t 7 / s
b. posisi sudut saat t 7 0 s
#. ke#epatan sudut rata-rata dari t 7 / s hingga t 7 0 s
Drs. Pristiadi Utomo, M.Pd. 00
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
34/45
Drs. Pristiadi Utomo, M.Pd.
d. ke#epatan sudut saat t 7 0 s
8a9a' )
a. 4 7 (2 (/*2< >* 7 > rad
b. 4 7 (2 (0*2< >* 7 20 rad
#. 7t
7
*/0(
*>20(
7 ; radHs
d. Z 7dt
d7 ( t * 7 ( . 0 * 7 12 radHs
0. %osisi sudut sebuah titik yang bergerak melingkar pada tepi sebuah roda adalah3
4 7 ( t0< > t2< 2 t < ; * rad
entukan 3
a. "e#epatan sudut rata-rata dari t 7 / hingga t 7 s
b. %er#epatan sudut rata-rata dari t 7 / hingga t 7 s
#. "e#epatan sudut saat t 7 2 s
d. %er#epatan sudut saat t 7 2 s
&aab 3
4 7 ( t0< > t2< 2 t < ; * rad
Z 7 (12 t2< 1/ t < 2 * radHs
X 7 (2 t < 1/ * radHs2
a. 4 7 ( t0< > t2< 2 t < ; * rad
41 7 ( ./0< > ./2< 2 ./ < ; * rad 7 ; rad
42 7 (. 0< > .2< 2 . < ; * rad 7 0>/ rad
7t
7
*/(
*;0>/(
7 :; radHs
b. Z 7 (12 t2< 1/ t < 2 * radHs
Z1 7 (12./2< 1/./ < 2 * radHs 7 2 radHs
Z2 7 (12.2< 1/. < 2 * radHs 7 20 radHs
7t
7
*/(
*220(
7 >: radHs2
#. Z 7 (12 .22< 1/ . 2 < 2 * 7 8/ radHs
d. X 7 (2. 2 < 1/ * 7 >: radHs2
0/i Kompetensi
1. %osisi sudut sebuah titik yang berada pada ujung roda sepeda ditentukan olehpersamaan 3
4 7 (2 t0< 2t* rad, maka tentukan 3
a. posisi sudut saat t 7 0 s
b. posisi sudut saat t 7 s
Drs. Pristiadi Utomo, M.Pd. 0
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
35/45
Drs. Pristiadi Utomo, M.Pd.
#. ke#epatan sudut rata-rata dari t 7 0 s hingga t 7 s
d. ke#epatan sudut saat t 7 2 s
e. persamaan per#epatan sudut sebagai $ungsi aktu
2. %osisi sudut sebuah titik yang bergerak melingkar pada terpi sebuah roda adalah3
4 7 ( t0< t2< t < 1 * rad
entukan 3
a. "e#epatan sudut rata-rata dari t 7 1 hingga t 7 2 s
b. %er#epatan sudut rata-rata dari t 7 1 hingga t 7 2 s
#. "e#epatan sudut saat t 7 1 s
d. %er#epatan sudut saat t 7 1 s
0. ebuah roda mobil mula-mula diam, kemudian dalam 0 sekon diper#epat sehingga
menempuh sudut 2 putaran. entukan besar ke#epatan sudut setelah 0 sekon danke#epatan sudut rata-ratanya
. ebuah roda sepeda mula-mula diam, kemudian dalam 2 sekon diper#epat sehingga
menempuh sudut putaran. entukan besar ke#epatan sudut rata-ratanya!
>. &ika posisi sudut dari suatu gerak melingkar beraturan dirumuskan dalam
persamaan 4 7 (;
> t0< > t2< * rad, maka tentukan ke#epatan sudut saat t 7
sekon!
Peker/aan R#ma%
akukan pengamatan terhadap beberapa gerak melingkar sebagai berikut bersama
kelompokmu !
1. 6erakan roda sepeda yang berjalan mengelilingi lapangan sekolah.
2. 6erakan kipas angin.
0. Amati juga tiga gerak melingkar lainnya di sekitarmu. Buatlah analisis dari gerakan-gerakan tersebut dan buatlah kesimpulannya!
Apakah gerakan-gerakan tersebut memiliki karakteristik gerakan yang sama
Pen$inte$ra"an >#n$si pada Gerak Me"in$kar
%osisi sudut 4 suatu $ungsi dapat juga ditentukan dari pengintegralan persamaan
ke#epatan sudut dengan rumus 3
4 7 4/< t dt
%ersamaan ke#epatan sudut dapat ditentukan dengan pengintegral persamaan per#epatan
sudut.
Drs. Pristiadi Utomo, M.Pd. 0>
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
36/45
Drs. Pristiadi Utomo, M.Pd.
7 /< t dt
(onto%)
1. &ika ke#epatan sudut sebuah roda dinyatakan dalam sebuah persamaan 3
Z 7 (0 t2< t * radHs, tentukan3
a. ke#epatan sudut saat t 7 1 s
b. ke#epatan sudut saat t 7 s
#. per#epatan sudut rata-rata dari t 7 1 s hingga t 7 s
d. per#epatan sudut saat t 7 > s
e. posisi sudut saat t 7 2 s, jika posisi sudut aal 2 rad
8a9a' )
a. Z 7 (0 (1*2< 1 * 7 radHs
b. Z 7 (0 (*2< * 7 >2 radHs
#. 7t
7
*1(
*>2(
7 1; radHs
d.dt
d= 7 (; t < 1* maka saat t 7 > s besar
e. 4 7 4o< + dttt *0(2
4 7 2 < t0< P t2, saat t 7 2 s, maka diperoleh
4 7 12 rad
2. "e#epatan sudut sebuah roda dinyatakan dalam sebuah persamaan 3
Z 7 ( t0< 2t * radHs, maka tentukan 3
a. ke#epatan sudut saat t 7 1 s
b. ke#epatan sudut saat t 7 2 s
#. per#epatan sudut rata-rata dari t 7 1 s hingga t 7 2 s
d. per#epatan sudut saat t 7 2 s
e. posisi sudut saat t 7 2 s, jika posisi sudut aal > rad
8a9a' )
a. Z 7 ( (1*0< 2.1 * 7 ; radHs
b. Z 7 ( (2*0< 2.2 * 7 0; radHs
#. 7t
7
*12(
*;0;(
7 0/ radHs2
d.dt
d= 7 (12 t 2< 2* maka saat t 7 2 s besar
7 (12 2 2< 2* 7 >/ radHs2
e. 4 7 4o< + dttt *2.(0
4 7 > < t< t2, saat t 7 2 s, maka diperoleh
Drs. Pristiadi Utomo, M.Pd. 0;
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
37/45
Drs. Pristiadi Utomo, M.Pd.
4 7 2> rad
0/i Kompetensi
1. "e#epatan sudut sebuah roda dinyatakan dalam sebuah persamaan 3
Z 7 ( t0 < 2t
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
38/45
Drs. Pristiadi Utomo, M.Pd.
a. @ektor posisi aal (saat t 7 / s*
b. @ektor perpindahan dari t 7 2 s hingga t 7 s
#. Besar vektor perpindahannya
8. @ektor posisi dari titik Rdinyatakan dalam vektor posisi yang mengandung unsur
aktu, yaitu3 r 7 2t i < t2j. entukan3
a. vektor perpindahan dari t 7 1 s hingga t 7 2 s
b. besar vektor perpindahan
:. @ektor posisi 6dinyatakan dalam r 7 (2 < 0t* i < 2t2j. entukan besar vektor
perpindahannya dari t 7 / s hingga t 7 8 s !
I. @ektor posisi Adinyatakan dalam r 7 t2i 0 j. entukan vektor perpindahan dan
arah perpindahannya dari t 7 1 s hingga t 7 > s !
1/. itik materi Tpada detik t 7 1 s berada pada posisi (2,/* m dan pada t 7 s beradapada posisi (:,:* m. entukan3
a. vektor ke#epatan rata-ratanya
b. besar vektor ke#epatan rata-rata
11. itik Imelakukan perpindahan dengan vektor perpindahan3
r7 ( 2 t 2i< > t/* m.
entukan 3
a. vektor ke#epatan saat t 7 2 s
b. besar ke#epatan saat t 7 2 s
12. Fndah melempar benda dengan persamaan ke#epatan v 7 (2t2 12* mHs.entukan
perpindahan dan jarak antara t 7 / hingga t 7 s !
10. Oitri mengendarai sepeda dengan ke#epatan seperti gra$ik berikut 3
entukan 3
a. &arak yang ditempuh setelah sepeda Oitri bergerak 8 s
b. &arak total yang ditempuh Oitri selama : s1. %artikel Dmelakukan perpindahan sesuai vektor perpindahan 3
r7 ( 2 t2i< t/* m. entukan 3
a. @ektor ke#epatan sebagai $ungsi aktu
b. Besar vektor ke#epatan saat t 7 2 s
Drs. Pristiadi Utomo, M.Pd. 0:
6ra$ik hubungan v dan t yangmenggambarkan gerakan sepedayang dilakukan Oitri
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
39/45
Drs. Pristiadi Utomo, M.Pd.
1>. itik materi Imelakukan gerak sesuai gra$ik berikut.
entukan 3
a. &arak yang ditempuh setelah t 7 1 sb. &arak yang ditempuh setelah t 7 0 s
#. &arak yang ditempuh setelah t 7 >,> s
1;. %ak "arta menaiki motor dengan persamaan ke#epatan
,7 ( 2t2i< : t/ * mHs entukan3
a. vektor per#epatan rata-rata dari t 7 1 s hingga t 7 0 s
b. besar per#epatan rata-rata dari t 7 1 s hingga t 7 0 s
18. %er#epatan yang dimiliki motor Dydy adalah a7 t2i : 0 t2/
&ika ke#epatan aal motor Dydy adalah nol, tentukan ke#epatan motor Dydy saat
t 7 2 s !
1:. uatu benda dari keadaan diam dan mengalami per#epatan seperti gra$ik berikut ini.
entukan ke#epatan saat > s !
1I. ebuah titik D melakukan perpindahan yang ditunjukkan dengan vektor
perpindahan sebagai berikut3
r7 (2 t2< 0 t* i< (1 < 2 t0*/ m
entukan3
a. vektor ke#epatan saat t 7 s
b. vektor per#epatan saat t 7 2 s
2/. ebuah bola ditendang Akmal dengan sudut elevasi >9 dan ke#epatan aal
/ mHs. entukan3
Drs. Pristiadi Utomo, M.Pd. 0I
6ra$ik v - t
6ra$ik a t untuk menentukanke#epatan sesaat
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
40/45
Drs. Pristiadi Utomo, M.Pd.
a. koordinat titik tertinggi
b. koordinat titik terjauh
21. &ika bola ditendang dengan ke#epatan aal 2/ mHs sehingga mengenai dinding
setinggi / m dan jarak mendatar / m, maka tentukan sudut elevasinya!
22. &ika ambuhan menembakkan peluru dengan sudut elevasi >9 dan ke#epatan aal
2// mHs, maka tentukan koordinat titik terjauhnya!
20. &ika 5a$id= melempar bola dengan vektor posisi r7 : t i< (2 t2 -2*/, maka
tentukan vektor posisi titik tertinggi yang di#apai bola.
2. %osisi sebuah sudut ditentukan oleh persamaan3
4 7 ( t2< >* rad, maka tentukan 3
a. posisi sudut saat t 7 / s
b. posisi sudut saat t 7 0 s#. ke#epatan sudut rata-rata dari t 7 / s hingga t 7 0 s
d. ke#epatan sudut saat t 7 0 s
2>. %osisi sudut sebuah titik yang bergerak melingkar dinyatakan3
4 7 (2 t0< 0 t2< 2 t < 2 * rad
entukan 3
a. "e#epatan sudut rata-rata dari t 7 / hingga t 7 s
b. %er#epatan sudut rata-rata dari t 7 / hingga t 7 s
#. "e#epatan sudut saat t 7 2 s
d. %er#epatan sudut saat t 7 2 s
Soa" Pi"i%an Ganda
Pi"i%"a% /a9a'an 5an$ 'enar2
1. eorang anak mengendarai sepeda sejauh 0 km dengan arah 0/9 timur laut. &ika
arah timur dijadikan sumbu ) positi$ maka notasi vektor perpindahannya adalah....
a. r7 (1,> 0 i< 1,>/* d. r7 (0 0 i< 1,> 0 /*
b. r7 (2,> 0 i< 1,>/* e. r7 (0 0 i< 0/*
#. r7 (0 0 i< 1,>/*
2. %osisi dari suatu partikel memenuhi persamaan r7 2t < t2dengan r dalam meter dan
t dalam sekon. "e#epatan partikel saat t 7 > sekon adalah ....
a. 0 mHs d. 12 mHs
b. > mHs e. 1> mHs
#. : mHs0. ebuah sepeda bergerak dengan ke#epatan 2/ mHs dalam arah 21/9 berlaanan
dengan arah jarum jam terhadap sumbu ) positi$. "omponen vektor ke#epatan
terhadap sumbu ) dan sumbu y adalah ....
a. vx7 -1/ mHs vy7 - > mHs d. vx7 -1/ 0 mHs vy7 - : mHs
Drs. Pristiadi Utomo, M.Pd. /
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
41/45
Drs. Pristiadi Utomo, M.Pd.
b. vx7 -1/ 0 mHs vy7 - > mHs e. vx7 -1/ 0 mHs vy7 - 1/ mHs
#. vx7 -12 0 mHs vy7 - ; mHs
. ebuah sepeda motor bergerak dalam sebuah ke#epatan yang dilukiskan dengan
gra$ik ke#epatan terhadap aktu berikut ini3
Besar perpindahan sepeda motor selama 1> sekon adalah ....
a. / m d. // m
b. 1// m e. >// m#. 1>/ m
>. %osisi ketinggian sebuah balon udara dinyatakan dalam persamaan 3 y 7 2/ t >t2,
dengan y dalam meter dan t dalam sekon. "e#epatan aal balon adalah ....
a. 2 mHs d. 2/ mHs
b. > mHs e. >/ mHs
#. 1/ mHs
;. ebuah mobil mainan bergerak dengan persamaan ke#epatan v 7 0t
2
;t I,dimana v dalam mHs dan t dalam sekon. &arak yang ditempuh mobil mainan antara t
7 1 s hingga t 7 sekon adalah ....
a. 1/ m d. > m
b. 2/ m e. 8,> m
#. 20 m
8. ebuah sepeda motor bergerak dengan
ke#epatan yang digambarkan seperti
gra$ik di samping.
Besar per#epatan saat t 7 12 sekon
adalah ....
a. - 2 mHs2
b. - > mHs2
#. - : mHs2
d. -1/ mHs2
e. -12 mHs2
:. eekor burung terbang dengan persamaan lintasan y 7 28 t t0, di mana y dalam
meter dan t dalam sekon. inggi maksimum burung adalah ....
a. 1/: m d. 28 m
b. :1 m e. 0 m
Drs. Pristiadi Utomo, M.Pd. 1
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
42/45
Drs. Pristiadi Utomo, M.Pd.
#. > m
I. ebuah peluru ditembakkan sehingga mempunyai persamaan perpindahan sebagai
berikut 3 r7 0/ t i< (0/ 0 t > t2*/, dengan rdalam meter, t dalam sekon, tinggi
maksimum yang di#apai peluru adalah ....
a. 10> m d. 1:/ 0 m
b. 10> 0 m e. 28/ m
#. 1:/ m
1/. ebuah benda bergerak dengan persamaan ke#epatan v =2t < > , di mana v dalam
mHs dan t dalam sekon. Bila saat t 7 / benda berada pada ) 7 m, maka posisi
benda saat t 7 s adalah ....
a. 2/ m d. 0> m
b. 2> m e. / m#. 0/ m
11. Coda sepeda berputar pada porosnya dengan persamaan posisi sudut 4 7 0 t < 2 t2,
di mana 4 dalam radian, dan t dalam sekon. %osisi sudut saat t 7 2 sekon adalah ....
a. 0 rad d. 1 rad
b. > rad e. 1: rad
#. 12 rad
12. &ika roda mobil berputar dengan persamaan posisi sudut 4 7 2 t < 2 t2
, di mana 4dalam radian, dan t dalam sekon, maka ke#epatan sudut roda mobil saat t 7 2 sekon
adalah ...
a. radHs d. 12 radHs
b. 8 radHs e. 1> radHs
#. 1/ radHs
10. &ika persamaan ke#epatan sudut suatu gerak melingkar dinyatakan dalam Z 7 0
t2< 2 t < 2, di mana Z dalam radHs dan t dalam sekon, jika posisi sudut aal gerak
melingkar 2 rad, maka posisi sudut gerak melingkar saat t 7 1 s adalah ....
a. ; rad d. 0 rad
b. > rad e. 2 rad
#. rad
1. ebuah peluru yang ditembakkan dengan ke#epatan aal vo dan sudut elevasi X
pada saat men#apai tinggi maksimum ...
a. tenaga kinetiknya maksimum
b. tenaga potensialnya maksimum#. tenaga potensialnya minimum
d. tenaga totalnya maksimum
e. ke#epatannya maksimum
Drs. Pristiadi Utomo, M.Pd. 2
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
43/45
Drs. Pristiadi Utomo, M.Pd.
1>. erhadap koordinat ) horisontal dan y vertikal, sebuah benda yang bergerak
mengikuti gerak peluru mempunyai komponen-komponen ke#epatan yang ....
a. besarnya tetap pada arah ) dan berubah-ubah pada sumbu y
b. besarnya tetap pada arah y dan berubah-ubah pada arah )
#. besarnya tetap, baik pada arah ) maupun pada arah y
d. besarnya berubah-ubah, baik pada arah ) maupun pada arah y
e. besar dan arah terus-menerus berubah terhadap aktu
1;. ebuah kapal laut sejauh 1/ km dengan arah >09 timur laut. &ika arah timur
dijadikan sumbu ) positi$, maka vektor perpindahannya adalah....
a. r 7 (/,; i < /,: j* d. r 7 (;/ i < :/ j*
b. r 7 (/,: i < /,; j* e. r 7 (:/ i < ;/ j*
#. r 7 (; i < : j *18. %osisi suatu partikel memenuhi persamaan r7 0t < 2t2dengan r dalam meter dan t
dalam sekon."e#epatan partikel saat t 7 > sekon adalah ....
a. 2: mHs d. 1> mHs
b. 2> mHs e. 12 mHs
#. 20 mHs
1:. %osisi ketinggian sebuah balon udara dinyatakan dalam persamaan 3 y 7 >/ t >t2,
dengan y dalam meter dan t dalam sekon. "e#epatan aal balon adalah ....
a. 2 mHs d. 2/ mHs
b. > mHs e. >/ mHs
#. 1/ mHs
1I. ebuah anak panah melun#ur dengan persamaan ke#epatan v 7 0t2 ;t I, dimana
v dalam mHs dan t dalam s. &arak yang ditempuh mobil mainan antara t 7 1 s hingga
t 7 sekon adalah ....
a. 1/ m d. > m
b. 2/ m e. 8,> m
#. 20 m
2/. eekor burung terbang dengan persamaan lintasan y 7 2/ t t2, dimana y dalam
meter dan t dalam sekon. inggi maksimum burung adalah ....
a. 1// m d. 1; m
b. 2/ m e. 0 m
#. 1I m
21. ebuah peluru ditembakkan sehingga mempunyai persamaan perpindahan sebagaiberikut 3 r7 0/ t i< (2/ t > t2* /, dengan rdalam meter, t dalam sekon, tinggi
maksimum yang di#apai peluru adalah ....
a. 10 m d. :/ m
b. 2/ m e. 2// m
Drs. Pristiadi Utomo, M.Pd. 0
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
44/45
Drs. Pristiadi Utomo, M.Pd.
#. ;/ m
22. ebuah benda bergerak dengan persamaan ke#epatan v =2t < 1/ , dimana v dalam
mHs dan t dalam sekon. Bila saat t 7 / benda berada pada ) 7 ; m, maka posisi
benda saat t 7 2 s adalah ....
a. 2/ m d. 0> m
b. 2> m e. / m
#. 0/ m
20. Coda sepeda berputar pada porosnya dengan persamaan posisi sudut 4 7 t < 2 t 2,
dimana 4 dalam radian, dan t dalam sekon. %osisi sudut ketika ke#epatan sudut
men#apai maksimum adalah adalah ....
a. 0 rad d. 1 rad
b. ; rad e. 1: rad#. 12 rad
2 . &ika persamaan ke#epatan sudut suatu gerak melingkar dinyatakan dalam Z 7 0 t2 rad e. 2 rad
#. rad
2>. 6erak sebuah benda memiliki persamaan posisi r 7 (:t * i < (-0t2< ; t *. emua
besaranmenggunakan satuan dasar F. Dari pernyataan berikut 3
1. benda bergerak lurus berubah beraturan
2. memiliki koordinat aal ( -, /*m
0. setelah 1 s perpindahannya > m
. setelah 1 s ke#epatannya menjadi : mHs.
%ernyataan yang benar adalah 3
a. 1, 2 dan 0 #. 1 dan
b. 1 dan 0 d. 2 ,0 dan
e. 2 dan
2;. %osisi sudut sebuah partikel pada tepi sebuah roda yang sedang berputar dinyatakan
oleh 4 7 t 0 t2< t0 , dengan 4 dalam radian dan t dalam sekon. "e#epatan
sudut ratarata antara t 7 / sampai t 7 2 sekon adalah ...radHs
a. 1 b. 2 #.0 d. e. >
28. ebuah peluru ditembakan dengan sudut elevasi 08/
dan ke#epatan aal >/ mHs.Maka perbandingan tinggi peluru ketika t7 1s dan t 7 2s adalah .....
a. 1H> b. [ #. 0H d. 0H> e. >H:
Drs. Pristiadi Utomo, M.Pd.
-
8/11/2019 Fisika Kelas Xi Kinematika Dengan Analisis Vektor
45/45
Drs. Pristiadi Utomo, M.Pd.
2:. ebuah 2 bola kasti menggelinding masing-masing ke#epatan v1dan v2dengan arah
mendatar jatuh dari lantai satu h17 2h dan lantai dua h270h. Membentuk lintasan
parabola. Maka perbandingan v1Hv2 adalah ......
a. 2H0 . b. 0H2 . #. 0 H2 d.2 0 H0 e. 1
2I. uatu benda dikatakan bergerak melingkar beraturan bila ....
1. perpindahannya konstan
2. ke#epatan sudutnya konstan
0. momentum liniernya konstan
.per#epatan sudutnya konsta
%ernyataan yang benar adalah ...
a. 1, 2 dan 0 b. 1 dan0 #. 2 dan d. e. 1, 2 , 0 dan
0/. ebuah peluru ditembakkan dengan arah horisontal dan dengan ke#epatan aal vdari ketinggian aal h dari permukaan tanah. &arak horisontal yang ditempuh
peluru tergantung pada ....
1. ke#epatan aal v
2. ketinggian h
0. per#epatan gravitasi
. massa peluru
%ernyataan yang benar adalah 3a. 1, 2 dan 0 b. 1 dan0 #. 2 dan d. e. 1, 2 , 0 dan