GETARAN MEKANIS 19 - finahari.files.wordpress.com posisi – waktu tampak sebagai kurva sinus...

GETARAN MEKANIS 19

Sistem mekanis mungkin mengalami getaran bebas atau bisa juga menjadi

subyek dari getaran paksa. Suatu getaran dikatakan ‘teredam’ jika gaya gesek terjadi dan ‘tidak teredam’ jika hal sebaliknya terjadi. Sistem suspensi truk secara esensial terdiri atas pegas-pegas dan ‘shock absorber’ yang menyebabkan bodi truk mengalami getaran paksa ‘teredam’ pada saat roda-rodanya dikenai gaya-gaya periodik pada sistem uji dinamis kendaraan sebagaimana tampak pada gambar.

~ Getaran Mekanis ~

Diterjemahkan oleh : Nurida F. 2

GETARAN MEKANIS

19.1. Pendahuluan

Getaran Tanpa Redaman

19.2. Getaran Bebas Partikel

Gerak Harmonis Sederhana

19.3. Pendulum Sederhana (Penyelesaian Pendekatan)

19.4. Pendulum Sederhana (Penyelesaian Eksak)

19.5. Getaran Bebas Benda Kaku

19.6. Penerapan Prinsip Konservasi Energi

19.7. Getaran Paksa

Getaran Teredam

19.8. Getaran Bebas Teredam

19.9. Getaran Paksa Teredam

19.10. Analogi Elektrik

19.1. PENDAHULUAN

Getaran mekanis adalah gerak partikel atau bodi yang berosilasi di sekitar posisi

keseimbangan. Pada umumnya getaran pada mesin dan struktur tidak diinginkan terjadi

karena adanya peningkatan tegangan dan hilangnya energi sebagai akibatnya. Itulah

sebabnya maka getaran harus dihilangkan atau dikurangi sejauh mungkin melalui desain

yang tersedia. Analisa getaran menjadi semakin penting pada tahun-tahun terakhir

sejalan dengan tren masa kini yang mengarah pada mesin berkecepatan tinggi dan

struktur yang semakin ringan. Terdapat beberapa alasan untuk dapat berharap bahwa

tren tersebut akan berlanjut dan bahwa kebutuhan akan analisa getaran semakin besar di

masa yang akan datang.

Analisa getaran adalah subyek kajian yang sangat luas yang akan dibahas dalam

seluruh bab. Pembahasan awal kita akan dibatasi pada tipe-tipe getaran yang lebih

sederhana, yaitu getaran dari bodi atau sistem bodi dengan satu derajat kebebasan.

Getaran mekanis umumnya terjadi pada saat suatu sistem dilepas dari posisi

keseimbangan stabil. Sistem ini cenderung kembali pada posisi dibawah pembebanan

gaya-gaya potensial (bisa berupa gaya elastik atau gaya gravitasi untuk pendulum).

Namun umumnya sistem tersebut mencapai posisi orisinilnya dengan kecepatan tertentu

yang terjadi pada saat dilepas dari posisi dibawah keseimbangan. Selama proses

tersebut berlangsung terus tanpa batas, sistem tersebut terus bergerak bolak-balik

~ Getaran Mekanis ~


melalui posisi keseimbangan. Interval waktu yang dibutuhkan sistem untuk

menyelesaikan satu siklus gerak dinamakan frekuensi, dan pergeseran maksimum sistem

dari posisi keseimbangan dinamakan amplitudo getaran.

Jika gerakan yang terjadi hanya diakibatkan oleh gaya-gaya potensial saja,

getaran yang terjadi disebut getaran bebas (subbab 19.2 - 19.6). Jika satu gaya periodik

dikenakan pada sistem, gerakan yang terjadi disebut getaran paksa (subbab 19.7). Jika

efek gesekan dapat diabaikan, getaran dikatakan tidak teredam. Bagaimanapun

sebenarnya semua getaran adalah teredam dalam beberapa derajat. Jika getaran bebas

teredam sangat tipis, amplitudonya akan berkurang perlahan-lahan hingga, setelah

beberapa waktu tertentu, gerakannya berhenti. Tetapi jika redamannya cukup besar untuk

menahan getaran sesungguhnya, sistem tersebut kemudian secara perlahan dapat

mencapai posisi orisinilnya (subbab 19.8). Getaran paksa teredam terus berlangsung

selama gaya periodik yang menghasilkan getaran tersebut terus dikenakan. Amplitudo

getaran, bagaimanapun, dipengaruhi oleh kekuatan gaya redaman (subbab 19.9).

GETARAN TANPA REDAMAN

19.2. GETARAN BEBAS DARI PARTIKEL, GERAK HARMONIS SEDERHANA

Bayangkan satu bodi dengan massa m terpasang pada pegas dengan konstanta k

(Gambar 19.1a). Selama kita hanya mengacu pada gerakan pusat massa, kita berasumsi

bodi ini adalah partikel. Jika suatu partikel berada pada keseimbangan statis, gaya-gaya

yang bekerja padanya adalah berat W dan gaya T yang ditimbulkan oleh pegas, yang

besarnya T = k . st , dimana st menyatakan regangan pegas. Jadi diperoleh W = k . st.

Tidak

teregang

Keseimbangan

st

W

stkT

Keseimbanganx

O

-xm

+xm

P

W

)( xkT st

xmma

(a) (b)

Gambar 19.1.

~ Getaran Mekanis ~


Jika sekarang partikel ditarik sejauh xm dari posisi keseimbangan dan dilepaskan

tanpa kecepatan awal dengan anggapan bahwa xm dipilih lebih kecil dari st, partikel akan

bergerak maju dan mundur melalui titik keseimbangan; getaran dengan amplitudo xm telah

terjadi. Catat bahwa getaran juga dapat dibuat dengan memberikan kecepatan awal

tertentu pada partikel saat berada pada posisi keseimbangan x = 0, atau secara umum

memulai gerak partikel dari sembarang posisi yang ditentukan x = xo dengan kecepatan

awal vo.

Untuk menganalisa getaran, diasumsikan partikel berada pada posisi P di

sembarang waktu t (Gambar 19.1b).Dinyatakan dengan x, pergeseran OP diukur dari

posisi keseimbangan O (arah ke bawah positif), tampak bahwa gaya-gaya yang bekerja

pada partikel adalah berat W dan gaya T yang dihasilkan pegas dimana, pada posisi ini,

memiliki besar T = k . (st + x). Karena W = k . st dapat dilihat bahwa besar gaya resultan

F dari kedua gaya tersebut (ke bawah positif) adalah :

F = W - k . (st + x) = - k x 19-1)

Jadi resultan gaya yang bekerja pada partikel sebanding dengan jarak OP yang diukur

dari posisi keseimbangan. Mengacu pada konvensi tanda, F selalu mengarah pada posisi

keseimbangan O. Substitusikan F ke dalam persamaan fundamental F = m . a dan

mengacu bahwa a merupakan turunan kedua x dari x terhadap waktu t, maka diperoleh :

m x + k x = 0 19-2)

Catat bahwa konvensi tanda yang sama harus diberlakukan pada percepatan x dan

pergerakan x, yaitu ke bawah positif.

Gerak yang dinyatakan dengan persamaan 19-2) dinamakan Gerak Harmonis

Sederhana. Gerak ini dicirikan oleh fakta bahwa percepatan sebanding dengan

pergeseran dan berarah berlawanan. Kita akan buktikan bahwa fungsi tmkx /sin1

dan tmkx /cos2 memenuhi persamaan 19-2). Fungsi-fungsi ini, nantinya,

menyusun 2 penyelesaian partikular dengan konstanta sembarang dan dijumlahkan. Jadi

penyelesaian umum dinyatakan dengan :

x = C1 x1 + C2 x2 = C1 tmk /sin + C2 tmk /cos 19-3)

Di sini tampak bahwa x adalah fungsi periodik dari waktu dan juga menyatakan getaran

dari partikel P. Koefisien t yang kita peroleh dari rumusan di atas mengacu pada frekuensi

putar natural yang dinyatakan dengan n. Didapat,

Frekuensi putar natural = n = mk / 19-4)

Substitusi mk / pada persamaan 19-3) diperoleh :

x = C1 sin n t + C2 cos n t 19-5)

~ Getaran Mekanis ~


Ini adalah penyelesaian umum untuk persamaan diferensial

02 xx n 19-6)

Yang dapat diperoleh dari persamaan 19-2) dengan membagi masing-masing sisi dengan

m dan menuliskan 2

nmk . Diferensiasi dua kali persamaan 19-5) terhadap t akan

diperoleh rumusan untuk kecepatan dan percepatan pada waktu t :

v = x = C1 n cos n t - C2 n sin n t 19-7)

a = x = - C1 n 2 sin n t - C2 n

2 cos n t 19-8)

Nilai dari konstanta C1 dan C2 tergantung pada kondisi awal gerakan. Sebagai contoh,

diperoleh C1 = 0 jika partikel digerakkan dari posisi keseimbangan dan dilepas pada t = 0

tanpa kecepatan awal, dan diperoleh C2 = 0 jika partikel bergerak dari O pada t = 0

dengan kecepatan awal tertentu. Secara umum, masukkan nilai t = 0 dan nilai awal xo dan

vo dari pergerakan dan kecepatan ke dalam persamaan 19-5) dan 19-7) akan diperoleh

C1 = vo / n dan C2 = xo.

Rumusan-rumusan untuk posisi, kecepatan dan percepatan dari sebuah partikel

sebagaimana tertulis di atas dapat dituliskan dalam bentuk yang lebih ringkas jika

persamaan 19-5) ditinjau lebih lanjut yaitu bahwa posisi x = OP adalah jumlah dari

komponen-komponen vektor C1 dan C2 dari x, masing-masing dengan besaran C1 dan C2

yang berarah sebagaimana tampak pada gambar 19.2a.

O

P Q

C1

C2

tn

tnx

m

-xm

+xm

t

x

(a) (b)

Gambar 19.2.

~ Getaran Mekanis ~


Dengan t yang bervariasi, kedua vektor tersebut berputar berlawanan arah jarum

jam, dapat dicatat juga bahwa panjang resultan vektor QO sama dengan pergeseran

maksimum xm. Gerak harmonis sederhana dari P sepanjang sumbu x dapat ditunjukkan

dengan memproyeksikan pergerakan titik Q pada sumbu tersebut yang merupakan

sebuah lingkaran berjari-jari xm dengan kecepatan putar konstan n (yang menjelaskan

istilah dari frekuensi putar natural n). Dengan menunjuk sebagai sudut yang dibentuk

oleh vektor QO dan C1 dapat dituliskan :

OP = OQ sin (n t + ) 19-9)

Yang mengarah pada rumus baru untuk posisi, kecepatan dan percepatan dari P sebagai

berikut :

x = xm sin (n t + ) 19-10)

v = x = xm n cos (n t + ) 19-11)

a = x = - xm n 2 sin (n t + ) 19-12)

Grafik posisi – waktu tampak sebagai kurva sinus (gambar 19.2b); harga maksimum xm

dari pergeseran disebut amplitudo getaran, dan sudut yang menyatakan posisi awal Q

pada lingkaran disebut sudut fase. Dapat dilihat dari gambar 19.2 bahwa siklus utuh

tercapai jika sudut n t naik hingga 2 radian. Nilai t satu siklus dinyatakan dengan n

disebut perioda getaran bebas dan diukur dalam detik. Diperoleh :

Perioda = n = 2 / n 19-13)

Jumlah siklus per satuan waktu dinyatakan dengan fn , dikenal sebagai frekuensi natural

getaran. Ditulis :

Frekuensi natural = fn = 1/n = n / 2 19-14)

Unit frekuensi adalah frekuensi 1 siklus per detik, sesuai dengan perioda 1 s. Dalam

istilah satuan dasar, satuan frekuensi adalah 1/s atau s-1. Ini disebut Hertz (Hz) dalam

sistem satuan SI. Hal ini juga sesuai dengan rumus 19-14) bahwa frekuensi 1 s-1 atau 1

Hz sesuai dengan frekuensi putar 2 rad/s. Dalam permasalahan yang melibatkan

kecepatan putar yang dinyatakan dalam revolusi per menit (rpm), didapat bahwa 1 rpm =

1

60

1 s = Hz60

1 atau 1 rpm = (2 / 60) rad/s.

Kembali kepada n yang didefinisikan rumus 19-4) dalam variabel konstanta

pegas k dan massa m dari partikel, dapat dilihat bahwa perioda dan frekuensi tidak

tergantung pada posisi awal dan amplitudo getaran. Catat bahwa n dan fn lebih

dipengaruhi oleh massa dan bukan berat partikel sehingga tidak tergantung pada nilai g.

~ Getaran Mekanis ~


Grafik waktu – kecepatan dan waktu – percepatan dapat dinyatakan sebagai kurva

sinus dengan perioda yang sama dengan grafik waktu – posisi, tapi dengan sudut fase

yang berbeda. Dari persamaan 19-11) dan 19-12) dapat dicatat bahwa nilai maksimum

dari harga kecepatan dan percepatan adalah :

vm = xmn am = xmn2 19-15)

Selama titik Q mengikuti pola lingkaran berjari-jari xm dengan kecepatan putar konstan n,

kecepatan dan percepatannya sebagaimana terumuskan dalam persamaan 19-15).

Kembali pada persamaan 19-11) dan 19-12) diperoleh bahwa kecepatan dan percepatan

titik P dapat dihitung untuk setiap saat dengan memproyeksikan vektor dengan besaran

vm = xmn dan am = xmn2 pada sumbu x, yang menyatakan kecepatan dan percepatan titik

Q pada saat yang sama (gambar 19.3)

O

P

Q

tn

xm

Qo

tn

x a 2

nmm xa

nmm xv v

x

Gambar 19.3.

Hasil yang diperoleh tidak terbatas hanya untuk penyelesaian permasalahan

massa–pegas saja. Juga dapat digunakan untuk menganalisa gerak lurus partikel dimana

resultan F dari gaya-gaya yang bekerja pada partikel sebanding dengan pergerakan x dan

mengarah ke O. Persamaan gerak fundamental F = ma dapat dituliskan dalam bentuk

persamaan 19-6) yang menunjukkan karakteristik gerak harmonis sederhana. Mengacu

bahwa koefisien x harus sama dengan n2, maka dengan mudah dapat ditentukan

frekuensi putar natural dari gerak (n). Substitusikan nilai n dalam persamaan 19-13) dan

19-14) untuk menentukan perioda n dan frekuensi natural fn dari gerak.

~ Getaran Mekanis ~


19.3. PENDULUM SEDERHANA (PENYELESAIAN PENDEKATAN)

Pada umumnya getaran yang terjadi pada aplikasi teknis dapat dinyatakan

sebagai gerak harmonis sederhana. Kasus-kasus yang lain, meskipun berbeda tipe,

dapat didekati sebagai gerak harmonis sederhana selama amplitudo yang terjadi tetap

kecil. Misalnya, sebagai contoh sebuah pendulum sederhana, terdiri atas bola dengan

massa m tergantung pada tali dengan panjang yang dapat berosilasi pada bidang

vertikal (gambar 19.4a).

(a) (b)

m

W

T nam tam

Gambar 19.4.

Pada sembarang waktu t, tali membentuk sudut terhadap vertikal. Gaya-gaya

yang bekerja pada bola adalah berat W dan gaya T yang dihasilkan tali (gambar 19.4b).

Dengan menguraikan vektor ma menjadi komponen-komponen tangensial dan normal,

dimana mat mengarah ke kanan yaitu pada arah yang sesuai dengan pertambahan nilai

dan melihat bahwa at = = , dapat ditulis :

tt amF . ; .sin mW

Karena W = mg dan membagi persamaan dengan m akan diperoleh :

0sin

g 19-16)

Untuk osilasi amplitudo kecil, sin dan dinyatakan dalam radian maka :

0

g 19-17)

Jika dibandingkan dengan persamaan 19-16) dapat dilihat bahwa persamaan diferensial

19-17) adalah gerak harmonis sederhana dengan frekuensi putar natural n = (g/ )1/2.

Penyelesaian umum dari persamaan 19-17) dapat dinyatakan sebagai :

= m sin (nt + )

Dimana m adalah amplitudo getaran dan adalah sudut fase. Substitusikan nilai n pada

persamaan 19-13) akan diperoleh rumus perioda getaran pendulum dengan panjang :

gn

n

2

2 19-18)

~ Getaran Mekanis ~


*19.4. PENDULUM SEDERHANA (PENYELESAIAN EKSAK)

Persamaan 19-18) hanyalah pendekatan. Untuk mendapatkan persamaan eksak

dari perioda osilasi pendulum sederhana, kita harus kembali pada persamaan 19-16).

Kalikan kedua buah suku dengan 2 dan diintegrasi dari posisi awal sesuai dengan

defleksi maksimum, yaitu m dan , didapatkan

ml

g

dt

d

coscos

22

Gantilah cos dengan 2/sin21 2 dan mcos dengan suku yang sesuai, selesaikan

untuk dt dan integrasikan untuk seperempat periode dari t = 0, 0 ke 4/nt , m

akan diperoleh

m

m

n

d

g

022 2/sin2/sin

12

Integral pada suku sebelah kanan dikenal dengan integral eliptik; yang tidak dapat

dinyatakan dalam aljabar atau trigonometri biasa. Namun dengan membuat

sin2/sin2/sin m

Kita dapat menuliskan

2/

022 sin2/sin1

14

m

n

d

g 19-19)

Dimana integral yang diperoleh, umumnya dinotasikan dengan K, dapat dihitung

menggunakan integrasi metode numerik. Nilainya juga dapat ditemukan pada tabel

integral eliptik untuk berbagai variasi nilai 2/m . Untuk membandingkan hasil yang baru

saja diperoleh dengan subbab sebelumnya, kita tuliskan persamaan 19-19) dalam bentuk

g

lKn

2

2 19-20)

Persamaan 19-20) menunjukkan bahwa nilai aktual dari perioda pendulum sederhana

dapat diperoleh dengan mengalikan nilai pendekatan yang diberikan oleh persamaan 19-

18) dengan faktor koreksi 2K/. Nilai faktor koreksi diberikan pada tabel 19.1 untuk

berbagai nilai amplitudo m . Dapat dicatat bahwa untuk perhitungan teknik sehari-hari

faktor koreksi dapat digunakan sepanjang amplitudo tidak melebihi 10o.

~ Getaran Mekanis ~


Tabel 19.1. Faktor koreksi untuk perioda pendulum sederhana

m 0o 10o 20o 30o 60o 90o 120o 150o 180o

K 1.571 1.574 1.563 1.598 1.686 1.854 2.157 2.768

2K/ 1.000 1.002 1.008 1.017 1.073 1.180 1.373 1.762

Lihat, sebagai contoh, Tabel Matematika Standar, Chemical Rubber Publishing Company, Cleveland, Ohio

CONTOH SOAL 19-1

k1 = 4 kN/m

k2 = 6 kN/m

(a) (b)

Sebuah balok 50 kg bergerak diantara pengarah vertikal

sebagaimana tampak pada gambar. Balok tersebut

ditarik 40 mm ke bawah dari posisi keseimbangan dan

dilepas. Untuk setiap model pengaturan pegas, tentukan

perioda dari getaran, kecepatan maksimum dari balok

dan percepatan maksimumnya.

PENYELESAIAN :

a. Pegas terpasang paralel

1k 2k

P

Pertama tentukan dulu konstanta pegas tunggal yang

ekuivalen dengan 2 pegas tersebut dengan menentukan

besar gaya P yang dibutuhkan untuk menghasilkan

defleksi . Jika defleksi dihasilkan oleh gaya-gaya

pegas k1 dan k2, maka :

P = k1 + k2 = (k1 + k2)

Konstanta k dari pegas ekuivalen tunggal adalah :

k = P / = k1 + k2 = 4 kN/m + 6 kN/m = 10 kN/m = 104 N/m

Perioda getaran : Selama m = 50 kg, persamaan 19-4) menghasilkan,

14,1450

10 42

kgm

k mN

n rad/s n

n 2 n = 0,444 s

Kecepatan maksimum : vm = xmn = (0,04 m) (14,14 rad/s) vm = 0,566 m/s

Percepatan maksimum : am = xmn2 = (0,04 m) (14,14 rad/s)2 am = 8 m/s2

~ Getaran Mekanis ~


b. Pegas terpasang seri

1l

2l

11 l

22 l

P

Pertama tentukan dulu konstanta pegas tunggal yang ekuivalen

dengan 2 pegas tersebut dengan menentukan perpanjangan

pegas total di bawah beban statis P. Untuk memudahkan

perhitungan digunakan P = 12 kN maka :

= 1 + 2 = 56

12

4

12

21

m

kNm

kN

kNkN

k

P

k

P m

k = P / = 12 kN / 5 m = 2,4 kN/m = 2400 N/m

Perioda getaran : 93,650

24002 kgm

k mN

n rad/s n

n 2

n = 0,907 s

Kecepatan maksimum : vm = xmn = (0,04 m) (6,93 rad/s) vm = 0,277 m/s

Percepatan maksimum : am = xmn2 = (0,04 m) (6,93 rad/s)2 am = 1,920 m/s2

~ Getaran Mekanis ~


RINGKASAN UNTUK BELAJAR MANDIRI

Bab ini mempelajari getaran mekanis, yaitu gerak bolak-balik partikel atau benda

terhadap posisi keseimbangan. Pada pelajaran pertama, kita melihat bahwa getaran

bebas suatu partikel muncul jika partikel tersebut dikenai gaya yang sebanding dengan

perpindahannya dan berlawanan arah, seperti misalnya gaya yang ditimbulkan oleh

pegas (gambar 19.1). Gerak yang dihasilkan disebut gerak harmonis sederhana, yang

dicirikan oleh persamaan diferensial

0 xkxm 19-2)

Dimana x adalah perpindahan partikel, x adalah percepatannya, m adalah massanya dan

k adalah konstanta pegas. Penyelesaian persamaan diferensial ini diperoleh sebagai

berikut

txx nm sin 19-10)

Dimana xm = amplitudo getaran

n = mk / = frekuensi putar natural (rad/s)

= sudut fase (rad)

Kita juga mendefinisikan perioda getaran sebagai waktu nn /2 yang diperlukan

partikel untuk menyelesaikan satu siklus, dan frekuensi natural sebagai jumlah siklus per

detik, 2//1 nnnf , yang dinyatakan dalam Hertz atau s-1. Mendiferensiasi

persamaan 19-10) dua kali menghasilkan kecepatan dan percepatan partikel setiap saat.

Nilai kecepatan dan percepatan maksimum diperoleh sebagai berikut

2

nmmnmm xaxv 19-15)

Untuk menentukan parameter-parameter pada persamaan 19-10) dapat diikuti langkah-

langkah berikut.

1. Gambarkan diagram benda bebas yang menunjukkan gaya-gaya yang bekerja pada

partikel jika partikel itu terletak pada jarak x dari posisi keseimbangannya. Resultan

gaya-gaya akan sebanding dengan x dan arahnya akan berlawanan dengan arah

positif x [persamaan 19-1)].

2. Tuliskan persamaan diferensial dari gerak partikel dengan menyamakan gaya resultan

yang diperoleh pada langkah 1 dengan xm . Ingat bahwa sekali arah positif x telah

ditentukan, konvensi tanda yang sama harus diberlakukan untuk percepatan x .

Setelah pengaturan posisi suku-suku persamaan akan diperoleh bentuk persamaan

19-2)

~ Getaran Mekanis ~


3. Tentukan frekuensi putar natural n dengan membagi koefisien x dengan koefisien

x pada persamaan tadi lalu hitunglah nilai akar kuadrat hasilnya. Pastikan bahwa n

dinyatakan dalam rad/s

4. Tentukan amplitudo xm dan sudut fase dengan mensubstitusikan nilai n yang

diperoleh dan nilai awal x dan x dalam persamaan 19-10) dan persamaan yang

diperoleh dari difrensiasi 19-10) terhadap waktu t.

Persamaan 19-10) dan 2 persamaan lain yang diperoleh dari diferensiasi dua kali

terhadap waktu t, dapat digunakan untuk menentukan perpindahan, kecepatan dan

percepatan partikel setiap saat. Persamaan 19-15) menghasilkan kecepatan

maksimum mv dan percepatan maksimum ma .

5. Dapat dilihat juga bahwa untuk osilasi kecil dari pendulum sederhana, sudut yang

dibentuk oleh tali pendulum terhadap sumbu vertikal memenuhi persamaan diferensial

0 l

g 19-17)

dimana l adalah panjang tali dan dinyatakan dalam radian (subbab 19.3).

Persamaan ini menunjukkan kembali bentuk gerak harmonis sederhana dan

penyelesaiannya sama dengan persamaan 19-10),

tnm sin

dimana frekuensi putar natural lgn / dinyatakan dalam rad/s. Penentuan

beberapa konstanta pada persamaan ini diperoleh dengan cara yang sama seperti

diuraikan di atas. Ingat bahwa kecepatan dari bola pendulum sejajar garis singgung

jalur dan besarnya adalah lv , sedangkan percepatan pendulum memiliki

komponen tangensial at, dengan besar lat , dan komponen normal an yang

mengarah pada pusat lingkaran dengan besar 2lan .

~ Getaran Mekanis ~


SOAL – SOAL

19.1. Tentukan kecepatan dan percepatan maksimum sebuah partikel yang bergerak

mengikuti gerak harmonis sederhana dengan amplitudo 400 mm dan perioda 1,4 s.

19.2. Tentukan amplitudo dan kecepatan maksimum partikel yang bergerak dalam gerak

harmonis sederhana dengan percepatan maksimum 6,5 m/s2 dan frekuensi 8 Hz.

19.3. Sebuah partikel bergerak dalam gerak harmonis sederhana. Jika diketahui bahwa

amplitudonya 375 mm dan percepatan maksimumnya 4,5 m/s2, tentukan kecepatan

maksimum partikel tersebut dan frekuensi geraknya.

19.4. Sebuah pendulum sederhana terdiri atas bola yang terpasang pada tali, berosilasi

pada bidang vertikal dengan perioda 1,3 s. Jika diasumsikan bergerak dalam gerak

harmonis sederhana dan diketahui bahwa kecepatan maksimum bola adalah 0,4 m/s,

tentukan (a) amplitudo gerak dalam derajat, (b) percepatan tangensial maksimum bola.

19.5. Sebuah pendulum sederhana terdiri atas bola yang terpasang pada tali dengan

panjang l = 1 m berosilasi pada bidang vertikal. Jika diasumsikan bergerak dalam gerak

harmonis sederhana dan diketahui bahwa bola dilepaskan dari posisi = 6o, tentukan (a)

frekuensi getaran, (b) kecepatan maksimum bola.

19.6. Sebuah balok 10 kg mula-mula disangga sehingga pegas yang terpasang

sebagaimana tampak pada gambar tidak terdeformasi. Jika balok tiba-tiba dilepaskan,

tentukan (a) amplitudo dan frekuensi gerak yang terjadi, (b) kecepatan dan percepatan

maksimum balok.

l

m

10 kg

16 kN/m

135 kN/m

32 kg

Gambar P19.4. dan P19.5. Gambar P19.6. Gambar P19.7.

19.7. Balok 32 kg dipasang pada pegas dan dapat bergerak tanpa gesekan dalam slot

sebagaimana tampak pada gambar. Balok berada pada posisi keseimbangan hingga

sebuah palu memukulnya dan memberikan kecepatan awal 3 m/s. Tentukan (a) perioda

dan frekuensi gerak yang terjadi, (b) amplitudo gerak dan percepatan maksimum balok.

~ Getaran Mekanis ~


19.8. Sebuah kotak peralatan A dibaut pada meja getar sebagaimana tampak pada

gambar. Meja bergerak vertikal dalam gerak harmonis sederhana dengan frekuensi yang

sama dengan variasi kecepatan motor penggeraknya. Kotak tersebut akan diuji pada

percepatan penuh 50 m/s2. Jika diketahui bahwa amplitudo meja getar 58 mm, tentukan

(a) kecepatan motor yang diperlukan dalam rpm, (b) kecepatan maksimum meja.

A

B k

135 kN/m

32 kg

Gambar P19.8. Gambar P19.9. Gambar P19.12.

19.9. Balok A seberat 5 kg diletakkan pada plat B seberat 20 kg yang dipasang pada

pegas tidak teregang dengan konstanta k = 900 N/m. Plat B bergerak 60 mm ke kiri dan

dilepas. Jika diasumsikan balok A tidak mengalami slip pada plat, tentukan (a) amplitudo

dan frekuensi gerak yang terjadi, (b) nilai koefisien gesek statis terkecil yang diijinkan.

19.10. Gerak sebuah partikel dinyatakan oleh persamaan x = 10 sin 2t + 8 cos 2t, dimana

x dinyatakan dalam ft dan t dalam detik. Tentukan (a) perioda gerak yang terjadi, (b)

amplitudonya, (c) sudut fasenya.

19.11. Gerak sebuah partikel dinyatakan oleh persamaan x = 0,2 cos 10t + 0,15 sin (10t

- ), dimana x dinyatakan dalam ft dan t dalam detik. Tentukan (a) perioda gerak yang

terjadi, (b) amplitudonya, (c) sudut fasenya.

19.12. Balok 32 kg dipasang pada pegas dengan konstanta 135 kN/m, dapat bergerak

tanpa gesekan pada slot sebagaimana tampak pada gambar. Balok diberi posisi awal 375

mm dari posisi keseimbangan dan dilepas. Tentukan 1,5 s setelah dilepas (a) total jarak

yang ditempuh balok, (b) percepatannya.

19.13. Balok 1,4 kg ditopang pegas dengan konstanta k = 400 N/m yang dapat bersifat

tarikan ataupun tekanan sebagaimana tampak pada gambar. Balok akan berada pada

posisi keseimbangan jika dipukul palu yang memberikan kecepatan ke atas sebesar 2,5

m/det. Tentukan (a) waktu yang diperlukan balok untuk bergerak 60 mm ke atas, (b)

kecepatan dan percepatan balok pada saat itu.

~ Getaran Mekanis ~


A

k

m

l

m

A

k

m

C

k

0,5 m

Gambar P19.13. Gambar P19.15. Gambar P19.16. Gambar P19.17.

19.14. Mengacu pada soal 19.13., tentukan posisi, kecepatan dan percepatan balok 0,9

det setelah dipukul palu.

19.15. Bola pendulum sederhana dengan panjang l = 1 m dilepaskan dari posisi diam

pada sudut = +5o. Jika diasumsikan bergerak harmonis sederhana, tentukan kondisi

setelah dilepas 1,6 detik (a) sudut , (b) kecepatan dan percepatan bola.

19.16. Sebuah silinder diletakkan, tanpa terikat, di atas pegas sebagaimana tampak pada

gambar. Diketahui bahwa jika silnder ditekan turun sejauh 225 mm atau lebih dan

dilepaskan, silinder tersebut akan kehilangan kontak dengan pegas. Tentukan (a)

konstanta pegas, (b) posisi, kecepatan dan percepatan silinder 0,16 detik setelah

dilepaskan.

19.17. Silinder C seberat 5 kg sebagaimana tampak pada gambar, dilepaskan dari posisi

diam dan meluncur tanpa gesekan pada tiang vertikal hingga mengenai dan menakan

pegas dengan konstanta k = 720 N/m. Kecepatan silinder berkurang hingga nol dan

silinder bergerak kembali ke posisi semula. Siklus selanjutnya berulang. Tentukan (a)

perioda gerak silinder, (b) kecepatan silinder 0,4 detik setelah dilepaskan (Ingat, ini

merupakan gerak periodik, tetapi bukan gerak harmonis sederhana).

50 kg

12 kN/m 12 kN/m

24 kN/m

50 kg

24 kN/m

24 kN/m

13,6 kg

2,1 kN/m

3,5 kN/m

2,8 kN/m


~ Getaran Mekanis ~


19.18. dan 19.19. Sebuah balok 50 kg dipasang pada susunan pegas sebagaimana

tampak pada gambar. Balok digerakkan ke bawah dari posisi keseimbangannya dan

dilepas. Jika diketahui amplitudo gerakan 60 mm, tentukan (a) perioda dan frekuensi

gerakan, (b) kecepatan dan percepatan maksimum balok.

19.20. Balok dengan berat 13,6 kg dipasang pada susunan pegas sebagaimana tampak

pada gambar. Jika balok digerakkan 44 mm dari posisi keseimbangannya ke bawah dan

dilepaskan, tentukan (a) perioda dan frekuensi gerakan yang terjadi, (b) kecepatan dan

percepatan maksimum dari balok.

19.21. Sebuah balok 4,5 kg dipasang pada sisi bawah pegas yang sisi atasnya diikat,

bergetar dengan perioda 6,8 detik. Jika diketahui konstanta k pegas berbanding terbalik

dengan panjangnya, tentukan perioda balok 2,7 kg yang dipasang ditengah-tengah pegas

yang sama yang diikat pada kedua ujungnya.

C

4,5 kg

BA

kkk

A

k1

k2

k2

A

k1

1k

13,5 kN/m

A


19.22. Balok 4,8 kg dipasang pada 3 buah pegas dengan susunan sebagaimana tampak

pada gambar. Konstanta masing-masing pegas adalah k. Pada posisi keseimbangan

gaya tarik pegas A, B dan C masing-masing adalah 1,5; 1,8 dan 1,5 kg. Balok bergerak

ke bawah sejauh 12,5 mm dari posisi keseimbangan dan dilepaskan. Jika diketahui

bahwa dalam pergerakan tersebut tarikan minimum pada pegas B adalah nol, tentukan

(a) konstanta pegas k, (b) frekuensi gerakan, (c) tekanan maksimum pada pegas A.

19.23. Dua buah pegas dengan konstanta k1 dan k2 disusun seri pada balok A yang

bergetar dalam gerak harmonis sederhana dengan perioda 5 detik. Jika pegas yang sama

disusun secara paralel pada balok yang sama, balok bergetar dengan perioda 2 detik.

Tentukan rasio k1 / k2 dari konstanta pegas tersebut.

~ Getaran Mekanis ~


19.24. Perioda getaran sistem sebagaimana tampak pada gambar adalah 0,7 detik.

Setelah pegas dengan konstanta k2 = 13,5 kN/m dilepaskan dari sistem, perioda getaran

menjadi 0,9 detik. Tentukan (a) konstanta k1, (b) berat balok A.

19.25. Perioda osilasi kecil sistem yang tampak pada gambar adalah 1,6 detik. Setelah

silinder seberat 6,3 kg diletakkan pada puncak silinder A, perioda getaran menjadi 2,1

detik. Tentukan (a) berat silinder A, (b) konstanta pegas k.

19.26. Perioda getaran sistem sebagaimana tampak pada gambar adalah 0,2 detik.

Setelah pegas dengan konstanta k2 = 3,5 kN/m dilepaskan dan balok A disambungkan

pada pegas dengan konstanta k1, perioda getaran menjadi 0,12 detik. Tentukan (a)

konstanta pegas k1 yang tersisa, (b) massa balok A.

19.27. Balok D 50 kg dipasang pada pegas dengan susunan sebagaimana tampak pada

gambar. Konstanta pegas semuanya k. Perioda getaran vertikal tidak berubah meskipun

balok D digantikan dengan balok lain seberat 60 kg, pegas A diganti dengan pegas yang

konstantanya kA dan 2 pegas lainnya tidak diubah. Jika perioda getaran 0,4 detik,

tentukan nilai k dan kA.

19.28. Dari mekanika material diketahui bahwa jika beban statik P diaplikasikan di ujung B

batang logam homogen dengan ujung A terikat, panjang batang akan meningkat sebesar

= PL / AE, dimana L adalah panjang batang mula-mula, A adalah luas penampang

lintang batang dan E adalah modulus elastisitas material. Jika diketahui L = 450 mm, E =

200 GPa dan diameter batang 8 mm, dengan mengabaikan berat batang, tentukan (a)

konstanta pegas ekuivalen dari batang, (b) frekuensi getaran vertikal balok dengan berat

W = 72 kg yang terpasang pada ujung B batang yang sama.

19.29. Dari mekanika material diketahui bahwa jika pada batang homogen, dengan luas

penampang seragam ditumpu sederhana di kedua ujungnya, dikenai beban statik P

ditengah-tengah panjangnya, defleksi A = PL3 / 48EI akan terjadi, dimana L adalah

panjang batang, E adalah modulus elastisitas dan I adalah momen inersia penampang

lintang batang. Jika diketahui bahwa L = 5 m, E = 200 GPa dan I = 20 x 10 -6 m4, tentukan

(a) konstanta pegas ekuivalen dari batang, (b) frekuensi getaran balok 750 kg yang

diletakkan di tengah batang. Abaikan massa batang dan asumsikan beban tetap terjadi

pada batang secara konstan.

~ Getaran Mekanis ~


19.30. 60 mm defleksi terukur secara langsung pada lantai 2 gedung setelah

pemasangan mesin seberat 6000 kg yang berputar akibat ketidakseimbangan rotor. Jika

diasumsikan defleksi yang terjadi sebanding dengan beban yang ditumpu, tentukan (a)

konstanta pegas ekuivalen dari lantai sistem tersebut, (b) kecepatan putaran mesin dalam

rpm yang harus dihindari agar tidak selaras dengan frekuensi natural lantai.

*19.31. Persamaan defleksi-gaya untuk pegas non-linier yang satu ujungnya terpasang

tetap adalah F = 4x1/2 dimana F adalah gaya dengan satuan N yang bekerja di ujung

lainnya dan x adalah defleksi dengan satuan m. (a) Tentukan defleksi xo jika 100 gram

balok dipasang pada pegas dan tercapai keseimbangan. (b) Jika diasumsikan bahwa

slope kurva gaya-defleksi pada titik pembebanan tersebut dapat digunakan sebagai

konstanta pegas ekuivalen, tentukan frekuensi getaran balok jika ditarik sedikit dari titik

keseimbangan dan dilepaskan.

19.32. Batang AB dipasang pada gantungan A dengan 2 buah pegas sebagaimana

tampak pada gambar. Konstanta pegas masing-masing adalah k. (a) Tentukan massa

balok C yang mengakibatkan getaran dengan perioda 4 detik. (b) Jika ujung B ditekan

sejauh 60 mm dan dilepaskan, tentukan kecepatan maksimum balok C. Abaikan massa

batang dan asumsikan bahwa tiap pegas dapat berfungsi tarik ataupun tekan.

19.33. Jika defleksi statis batang yang dikenai beban dinotasikan sebagai st, tunjukkan

bahwa frekuensi getaran beban akan sama dengan

st

gf

2

1

Abaikan massa batang dan asumsikan bahwa beban batang konstan.

*19.34. Jika integran pada persamaan 19-19) sub bab 19.4. diekspansikan pada deret

pangkat genap dari sin dan diintegrasi, tunjukkan bahwa perioda pendulum sederhana

dengan panjang l dapat didekati dengan rumusan

2sin

4

112 2 m

g

l

Dimana m adalah amplitudo osilasi.

*19.35. Menggunakan rumus yang diberikan pada soal 19.34, tentukan amplitudo m yang

menyebabkan perioda pendulum sederhana lebih panjang ¾ persen dari perioda

berosilasi kecil pendulum yang sama.

~ Getaran Mekanis ~


*19.36. Menggunakan data pada tabel 19.1., tentukan perioda pendulum sederhana

dengan panjang l = 600 mm (a) untuk osilasi kecil, (b) untuk osilasi dengan amplitudo m

= 30o, (c) untuk osilasi dengan amplitudo m = 120o.

*19.37. Menggunakan data pada tabel 19.1., tentukan panjang pendulum sederhana

dalam inchi, yang bergetar dengan perioda 3 detik dan amplitudo m = 60o.

~ Getaran Mekanis ~


19.5. GETARAN BEBAS BENDA KAKU

Analisa dari getaran benda kaku atau suatu sistem benda kaku yang memiliki satu

derajat kebebasan mirip dengan analisa getaran partikel. Beberapa variabel, seperti jarak

x atau sudut , dipilih untuk menentukan posisi dari benda atau sistem benda dan

persamaan yang menghubungkan variabel tersebut dengan turunan kedua terhadap

waktu t, dituliskan. Jika persamaan yang diperoleh memiliki bentuk yang sama dengan

persamaan 19-6), yaitu jika diperoleh

02 xx n atau 02 n 19-21)

Getaran yang terjadi adalah gerak harmonis sederhana. Perioda dan frekuensi natural

getaran tersebut dapat diperoleh dengan menentukan n dan mensubstitusikan nilainya

pada persamaan 19-13) dan 19-14).

Secara umum, cara sederhana untuk memperoleh persamaan 19-21) adalah

dengan menyatakan bahwa sistem gaya-gaya eksternal adalah sebanding dengan sistem

gaya-gaya efektif dengan menggambarkan persamaan diagram benda bebas untuk

sembarang nilai variabel dan menuliskan persamaan gerak yang bersesuaian. Proses ini

disebut sebagai Penentuan koefisien variabel x atau , bukan penentuan variabel itu

sendiri atau turunan x atau . Dengan menyamakan koefisien ini dengan 2

n akan

diperoleh frekuensi putar natural n , dimana n dan nf dapat ditentukan.

Metode di atas dapat digunakan untuk menganalisa getaran-getaran yang benar-

benar menunjukkan karakter gerak harmonis sederhana, atau getaran-getaran

beramplitudo kecil yang dapat didekati sebagai gerak harmonis sederhana. Sebagai

contoh, jika ditentukan perioda osilasi kecil sebuah plat segiempat bersisi 2b yang ditahan

di titik tengah O pada salah satu sisinya (Gb. 19.5a). Dipandang satu kondisi bahwa

posisi plat ditentukan dengan sudut yang dibentuk garis OG terhadap sumbu vertikal

dan digambarkan persamaan diagram benda bebas untuk menyatakan bahwa berat W

dari plat dan komponen-komponen Rx dan Ry dari reaksi pada titik O adalah ekuivalen

dengan vektor-vektor mat dan man juga ekuivalen dengan kopel I (Gb. 19.5b). Selama

kecepatan dan percepatan putar plat sama, yaitu dan , nilai kedua vektor tersebut

adalah mb dan 2mb , sedangkan momen kopelnya adalah I . Pada penerapan

metode ini sebelumnya (bab 16) telah dicoba kemungkinan untuk mengasumsikan arah

yang benar dari percepatan. Dalam hal ini, bagaimanapun, kita harus mengasumsikan

arah positif yang sama untuk dan agar diperoleh persamaan 19-21).

Konsekuensinya, percepatan putar diasumsikan positif jika berlawanan arah jarum jam

meskipun asumsi ini biasanya tidak realistis.

~ Getaran Mekanis ~


O

G

A

b

b

2b

3

5b

(a)

O

G

W

Ry

Rx

O

G

(b)

namtam

I

Gambar 19.5.

Dengan menyamakan momen-momen terhadap O akan diperoleh

+ IbmbbW )()sin(

Mengingat 2

3222

121 ])2()2[( mbbbmI dan W = mg , diperoleh

0sin5

3

b

g 19-22)

Untuk osilasi-osilasi amplitudo kecil, sin dapat diganti dengan , dinyatakan dalam

radian, sehingga

05

3

b

g 19-23)

Dibandingkan dengan persamaan 19-21) tampak bahwa persamaan yang diperoleh

adalah gerak harmonis sederhana dan frekuensi putar natural n osilasi ini adalah

21

)5/3( bg . Substitusi pada persamaan 19-13) akan menghasilkan perioda osilasi

g

b

n

n3

52

2

19-24)

Hasil yang diperoleh adalah valid hanya untuk osilasi-osilasi amplitudo kecil. Penjabaran

yang lebih akurat dari gerak plat diperoleh dengan membandingkan persamaan 19-16)

dan 19-22). Catat bahwa kedua persamaan tersebut identik jika dipilih l sama dengan

5b/3. Ini berarti bahwa plat akan berosilasi sebagai pendulum sederhana dengan panjang

l = 5b/3 dan hasil dari subbab 19.4 dapat digunakan untuk mengkoreksi nilai perioda yang

diperoleh dari persamaan 19-24). Titik A pada plat yang terletak pada garis OG dengan

jarak l = 5b/3 dari titik O dinamakan Pusat Osilasi terhadap O (Gb. 19.5a).

~ Getaran Mekanis ~


CONTOH SOAL 19-2

B

r

Sebuah silinder dengan berat W dan jari-jari r dipasang pada tali

sebagaimana tampak pada gambar. Salah satu ujung tali dipasang

pada sambungan kaku sementara ujung lainnya dihubungkan

dengan pegas yang memiliki konstanta pegas k. Tentukan perioda

dan frekuensi natural getaran silinder.

PENYELESAIAN :

Kinematika gerak. Pergeseran linier dan percepatan silinder dinyatakan dalam

pergeseran putar . Dipilih putaran searah jarum jam sebagai arah positif dan pergeseran

diukur dari posisi keseimbangan. Maka didapat

rx rx 22

rra (1)

B

Bx

a

I

am

T1

T2

2r

G

W

A A

Persamaan Gerak. Sistem gaya-gaya eksternal yang bekerja pada silinder terdiri atas

gaya berat W, gaya tarik tali T1 dan T2. Sistem ini ekuivalen dengan sistem gaya efektif

yang diwakili oleh vektor am pada G dan kopel I .

effAA MM )( IramrTWr )2(2 (2)

Pada saat silinder berada pada posisi keseimbangan, gaya tarik tali : To = ½ W. Jika

dinyatakan dalam variabel pergeseran putar , nilai T2 adalah :

)2(21

21

2 rkWkWkTT o (3)

Substitusi persamaan 1) dan 3) dalam 2) dengan mengingat bahwa 2

21 mrI diperoleh

2

21

21 )()2)(2( mrrrmrkrWWr

03

8

m

k yang merupakan ciri persamaan gerak harmonis sederhana, maka

m

kn

3

82 m

kn

3

8

k

m

n

n8

32

2

m

kf n

n3

8

2

1

2

~ Getaran Mekanis ~


CONTOH SOAL 19-3

Sebuah piringan bulat

PENYELESAIAN :

~ Getaran Mekanis ~



Dalam subbab ini dapat dilihat bahwa sebuah benda kaku, atau suatu sistem

benda kaku, dimana posisinya ditentukan oleh koordinat tunggal x atau , akan

menghasilkan gerak harmonis sederhana jika persamaan diferensial yang diperoleh dari

aplikasi Hukum Newton II berbentuk

02 xx n atau 02 n 19-21)

Tujuan yang harus dicapai adalah menentukan n, untuk menentukan perioda n dan

frekuensi natural nf . Dengan memberikan nilai untuk kondisi awal, persamaan gerak

dapat ditulis dalam bentuk

txx nm sin 19-10)

Dalam hal ini x dapat digantikan dengan jika melibatkan gerak putar. Untuk

menyelesaikan permasalahan pada subbab ini dapat diikuti langkah-langkah berikut.

1. Tentukan sistem koordinat yang digunakan untuk mengukur pergeseran benda dari

titik keseimbangannya. Dalam subbab ini akan ditemui banyak sekali permasalahan

yang melibatkan gerak putar benda terhadap satu sumbu tetap dan bahwa sudut yang

menunjukkan pergerakan benda dari posisi keseimbangan merupakan koordinat yang

paling memudahkan untuk digunakan. Pada permasalahan yang melibatkan gerak

datar suatu benda secara umum, dimana koordinat x (dan mungkin juga koordinat y)

digunakan untuk menentukan posisi pusat massa G dari benda, dan koordinat

digunakan untuk mengukur putaran terhadap G, temukan hubungan kinematis yang

memungkinkan untuk menyatakan x (dan y) dalam variabel [contoh soal 19.2].

2. Tuliskan persamaan diagram benda bebas untuk menyatakan bahwa sistem gaya-

gaya eksternal ekuivalen dengan sistem gaya-gaya efektif yang terdiri atas vektor

am dan kopel I , dimana xa dan . Pastikan bahwa setiap gaya atau kopel

yang bekerja digambarkan pada arah yang konsisten dengan pergerakan yang

diasumsikan dan bahwa tanda untuk a dan , secara berturut-turut, adalah pada arah

dimana koordinat x dan membesar.

3. Tuliskan persamaan diferensial gerak dengan menyamakan jumlah komponen gaya-

gaya eksternal dan gaya-gaya efektif pada arah x dan y, dan jumlah momen-momen

gaya tersebut terhadap titik yang ditentukan. Jika diperlukan, gunakan hubungan

kinematika yang diperoleh pada langkah 1 untuk mendapatkan persamaan yang

hanya menggunakan variabel . Jika merupakan sudut kecil, gantilah sin dengan

dan cos dengan 1, jika fungsi ini muncul pada persamaan. Dengan mengeliminasi

~ Getaran Mekanis ~


setiap reaksi yang tidak diketahui, akan diperoleh persamaan yang setipe dengan

persamaan 19.21). Catat bahwa dalam permasalahan yang melibatkan pergerakan

benda terhadap sumbu tetap, akan diperoleh persamaan dengan cepat melalui

penyamaan momen-momen gaya eksternal dan gaya efektif terhadap sumbu tersebut.

4. Bandingkan persamaan yang diperoleh dengan persamaan 19.21), sehingga dapat

diidentifikasi 2

n dan, sekaligus, dapat ditentukan frekuensi putar natural n . Ingat

bahwa obyek yang dianalisis tidak dapat diselesaikan dengan persamaan diferensial

tersebut, namun dalam hal ini persamaan yang diperoleh digunakan untuk

mengidentifikasi 2

n .

5. Tentukan amplitudo dan sudut fase , dengan mensubstitusikan nilai n yang

diperoleh, nilai awal koordinat dan turunan pertamanya pada persamaan 19.10) dan

persamaan yang diperoleh dari diferensiasi persamaan 19.10) terhadap t. Dari

persamaan 19.10) dan dua persamaan hasil diferensiasi dua kali terhadap t, serta

menggunakan hubungan kinematik yang didapatkan pada langkah 1, dapat ditentukan

posisi, kecepatan dan percepatan setiap titik pada benda di setiap waktu yang

ditentukan.

6. Pada permasalahan yang melibatkan getaran torsional, konstanta pegas torsional K

dinyatakan dalam N.m/rad atau lb.ft/rad. Perkalian K dengan sudut puntir , yang

dinyatakan dalam radian, menghasilkan momen kopel restorasi, yang harus

disamakan dengan jumlah momen gaya-gaya efektif, atau kopel terhadap sumbu

rotasi [contoh soal 19.3]

~ Getaran Mekanis ~


SOAL – SOAL

19.38. Batang homogen AC seberat 4,5 kg dipasang pada pegas yang memiliki konstanta

k = 750 N/m pada B dan k = 900 N/m pada C yang dapat bekerja pada kondisi tarik atau

tekan. Jika ujung C ditekan sedikit kemudian dilepaskan, tentukan (a) frekuensi getaran,

(b) amplitudo gerak di titik C, jika kecepatan maksimum pada titik tersebut 0,8 m/s.

19.39. Batang homogen AB seberat 9 kg dipasang pada pegas di titik A dan B yang

masing-masing memiliki konstanta 850 N/m dan dapat bekerja pada kondisi tarik atau

tekan. Jika ujung A ditekan sedikit kemudian dilepaskan, tentukan (a) frekuensi getaran,

(b) amplitudo gerak putar, jika kecepatan maksimum pada titik A 1,1 mm/s.

CBA

0,85 m

1,7 m

CB

A

360 mm600 mm

Gambar P19.38. Gambar P19.39.

~ Getaran Mekanis ~


19.6. PENERAPAN PRINSIP KONSERVASI ENERGI

Tampak pada subbab 19.2 bahwa jika sebuah partikel bermassa m berada dalam

gerak harmonis sederhana, resultant F dari gaya-gaya yang bekerja pada partikel

memiliki nilai yang sebanding dengan perpindahan x diukur dari posisi keseimbangan O

dan mengarah ke O; dituliskan F = - k x. Mengacu pada subbab 13.6, kita tulis F sebagai

Gaya Konservatif dan energi potensial yang bersesuaian dengannya adalah 2

21 kxV

dimana V diasumsikan sama dengan nol pada posisi keseimbangan x = 0. Jika kecepatan

partikel adalah x , energi kinetiknya adalah 2

21 xmT dan total energi partikel yang

dimiliki dapat dituliskan sebagai

T + V = konstan 2

212

21 kxxm konstan

Persamaan dibagi dengan m/2 dan mengacu pada subbab 19.2 bahwa 2/ nmk ,

dimana n adalah frekuensi putar natural dari getaran, didapat

222 xx n konstan 19-25)

Persamaan 19-25) adalah karakteristik dari gerak harmonis sederhana, dapat diperoleh

dari persamaan 19-16) dengan mengalikan kedua sisi dengan x2 dan diintegrasi.

Prinsip konservasi energi menghasilkan cara yang lebih mudah untuk menentukan

perioda getaran benda kaku atau sistem benda kaku dengan satu derajat kebebasan,

pada saat gerak sistem diidentifikasi sebagai gerak harmonis sederhana atau dapat

didekati sebagai gerak harmonis sederhana. Dengan memilih variabel, misalnya jarak x

atau sudut , dapat diambil 2 posisi sesaat sistem :

a. Pergeseran sistem mencapai maksimum : Didapat T1 = 0 dan V1 dapat dinyatakan

dalam xm atau m (dipilih V = 0 pada posisi keseimbangan)

b. Sistem melalui posisi keseimbangan : Didapat V2 = 0 dan T2 dapat dinyatakan dalam

kecepatan maksimum mx atau kecepatan sudut maksimum m

Selanjutnya dapat ditentukan total energi yang dihasilkan dan ditulis T1 + V1 = T2 + V2.

Mengacu dari persamaan 19-15) bahwa untuk gerak harmonis sederhana, kecepatan

maksimum sama dengan perkalian amplitudo dan frekuensi putar natural n , persamaan

ini dapat diselesaikan untuk memperoleh n .

Sebagai contoh, sekali lagi mari kita lihat plat segiempat pada subbab 19.5. Pada

posisi pergeseran maksimum (Gb. 19.6a) didapat

T1 = 0 )cos1()cos(1 mm WbbbWV

Atau untuk 2/)2/(sin2cos1 22

mmm untuk osilasi amplitudo kecil,

T1 = 0 2

21

1 mWbV 19-26)

~ Getaran Mekanis ~


Pada saat plat melewati posisi keseimbangan (Gb. 19.6b) kecepatannya maksimum dan

didapat

2

2122

212

212

21

2 mmmm ImbIvmT V2 = 0

Mengacu subbab 19.5 bahwa 2

32 mbI

22

35

21

2 )( mmbT V2 = 0 19-27)

Substitusi persamaan 19-26) dan 19-27) ke dalam T1 + V1 = T2 + V2, dan mengingat

kecepatan maksimum m adalah sama dengan hasilkali nm didapat

222

35

212

21 )( nmm mbWb 19-28)

Yang menghasilkan bgn 5/32 dan

g

b

n

n3

52

2

19-29)

Sebagaimana telah diperoleh.

O

G2

(b)

m

O

G1

W

(a)

0

mb cos

b

datum

W

b

datum

m

Gambar 19.6.

~ Getaran Mekanis ~


CONTOH SOAL 19-4

Rr

Tentukan perioda osilasi kecil sebuah silinder dengan

radius r yang berguling tanpa selip dalam permukaan

lengkung dengan radius R.

PENYELESAIAN :

G

Gh

mrR cos)( mR

r

datum

O

rR

Posisi 1

W Posisi 2

W

G

m

r

O

Posisi 2 C

m

mv

Sudut yang dibentuk oleh garis OG terhadap vertikal dinotasikan dengan . Selama

silinder berguling tanpa selip, prinsip konservasi energi dapat diterapkan pada posisi 1,

dimana = m dan pada posisi 2 dimana = 0.

Posisi 1 :

Energi kinetik T1 = 0 selama kecepatan silinder nol

Energi potensial. Dipilih datum sebagaimana tampak pada gambar. Jika W menyatakan

berat silinder, maka )cos1)((1 rRWWhV . Mengacu pada

kondisi osilasi kecil dimana 2/)2/(sin2)cos1( 22 maka

diperoleh 2

)(2

1

mrRWV

Posisi 2 :

Kecepatan sudut yang dibentuk garis OG pada saat silinder berada pada posisi 2

dinyatakan dengan m , dimana pusat rotasi sesaatnya berada pada titik C, maka dapat

dituliskan bahwa mm rRv )( m

m

mr

rR

r

v

~ Getaran Mekanis ~


Energi kinetik

2

212

21

2 mm IvmT

222

21

2122

21 ))(()( mm

r

rRmrrRm

22

43 )( mrRm

Energi potensial V2 = 0

Jadi Konservasi Energinya dapat ditulis :

T1 + V1 = T2 + V2

0)(2

)(0 22

43

2

m

m rRmrRW

Diketahui bahwa mnm dan W = mg, didapat :

22

43

2

)()(2

)( mn

m rRmrRmg

jadi rR

gn

3

22

karena n

n

2 maka

g

rRn

2

32

~ Getaran Mekanis ~



~ Getaran Mekanis ~


19.7. GETARAN PAKSA

Satu bentuk getaran yang sangat penting jika dipandang dari sisi penerapan di

bidang teknik adalah Getaran Paksa dari suatu sistem. Getaran ini terjadi jika suatu

sistem dikenai gaya periodik atau jika sistem tersebut dihubungkan secara elastis dengan

penyangga yang memiliki gerakan bolak-balik.

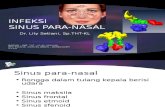
Foto 19.1. Sebuah seismograf yang bekerja dengan cara mengukur besaran energi listrik yang diperlukan untuk menjaga posisi massa agar tetap di tengah kotak pada saat terjadi getaran tanah yang kuat.

Perhatikan satu kasus dimana sebuah benda dengan massa m digantung pada

sebuah pegas dan dikenai gaya periodik P yang besarnya P = Pm sin ft, dimana f

adalah frekuensi putar dari P dan disebut dengan frekuensi putar paksa dari gerakan

tersebut (Gambar 19.7). Gaya ini mungkin berupa gaya luar aktual yang diaplikasikan

terhadap benda, atau mungkin berupa gaya sentrifugal yang diakibatkan oleh gerak rotasi

dari bagian benda yang tidak seimbang (lihat contoh soal 19.5).

Kesetimbanganx

PW

xkT st

tPP fm sinxmma

Gambar 19.7.

~ Getaran Mekanis ~


Dengan menotasikan x sebagai perpindahan benda yang diukur dari posisi seimbang,

maka persamaan geraknya dapat dituliskan sebagai berkut :

+F = ma; Pm sin f t + W – k(st + x) = m x

Dengan mengingat bahwa W = kst, maka :

m x + k x = Pm sin f t (19.30)

Selanjutnya kita perhatikan satu kasus dimana sebuah benda dengan massa m

digantung pada sebuah pegas yang diletakkan disebuah rangka yang bergerak dimana

perpindahan sama dengan m sin f t (Gambar 19.8). Pengukuran perpindahan x benda

tersebut dari posisi keseimbangan statis dimana f t = 0, didapat perpanjangan total

pegas pada waktu t adalah sebesar st + x - m sin f t. Persamaan geraknya menjadi :

+F = ma; W – k(st + x - m sin f t) = m x

Dengan mengingat bahwa W = kst, maka didapat :

m x + k x = km sin f t (19.31)

Kesetimbangan x

W

xmma

m tfm sin

tf0tf

txkT fmst sin

Gambar 19.8.

Perlu dicatat bahwa persamaan (19.30) dan (19.31) memilki bentuk yang sama

dan penyelesaian persamaan pertama akan juga menyelesaikan persamaan kedua jika

Pm = km. Persamaan differensial seperti persamaan (19.30) dan (19.31) memiliki suku

sisi kanan bukan nol, dan disebut dengan non-homogen. Penyelesaian umumnya didapat

~ Getaran Mekanis ~


dengan menambahkan penyelesaian khusus dari persamaan tersebut ke dalam

penyelesaian umum dari persamaan homogen yang bersesuaian (dimana suku sisi kanan

sama dengan nol). Penyelesaian khusus (partikular) dari persamaan (19.30) dan (19.31)

dapat diperoleh dengan mencoba penyelesaian berbentuk :

xpart = xm sin f t (19.32)

Substitusikan xpart untuk x ke persamaan (19.30) akandiperoleh :

-mf 2 xm sin f t + k xm sin f t = Pm sin f t

Yang dapat diselesaikan, untuk amplitudo :

2

f

mm

mk

Px

Dari persamaan (19.4) dimana k/m = n2, dimana n adalah frekuensi putar natural

sistem, maka :

2/1

/

nf

m

m

kPx

(19.33)

Substitusi persamaan (19.32) ke dalam persamaan (19.31) akan didapat penyelesaian

yang sejenis :

2/1 nf

m

mx

(19.33’)

Persamaan homogen yang bersesuaian dengan persamaan (19.30) atau (19.31) adalah

persamaan (19.2) yang mendefinisikan getaran bebas suatu benda. Penyelesaian

umumnya disebut dengan fungsi komplementer, dapat ditemukan pada sub bab 19.2 :

xcomp = C1 sin nt + C2 cos nt (19.34)

Dengan menambahkan penyelesaian khusus (19.32) ke persamaan komplementer

(19.34), kita akan memperoleh penyelesaian umum dari persamaan (19.30) dan (19.31) :

x = C1 sin nt + C2 cos nt + xm sin f t (19.35)

Perlu diingat bahwa getaran yang terjadi terdiri dari 2 buah getaran superposisi.

Dua suku pertama dalam persamaan (19.35) menggambarkan getaran bebas sistem.

Frekuensi getaran ini adalah frekuensi natural sistem yang hanya tergantung pada

konstanta pegas k dan massa benda m, sedangkan konstanta C1 dan C2 dapat diturunkan

dari kondisi awalnya (kondisi inisial). Getaran bebas ini juga disebut dengan getaran

transien, karena dalam aplikasinya getaran ini akan segera diredam oleh gaya gesek (sub

bab 19.9).

Suku terakhir pada persamaan (19.35) menggambarkan kondisi stedi getaran

yang dihasilkan yang disebabkan dan dijaga oleh gaya luar atau gerakan penyangga.

Frekuensinya adalah frekuensi paksa yang dihasilkan oleh gaya luar atau gerakan

~ Getaran Mekanis ~


penyangga tersebut dan amplitudo xm didefinisikan oleh persamaan (19.33) atau (19.33’),

tergantung pada rasio frekuensi f /n. Rasio dari amplitudo xm getaran kondisi stedi

terhadap defleksi statis Pm/k yang disebabkan oleh gaya Pm, atau terhadap amplitudo m

dari gerakan penyangga disebut faktor pembesaran. Dari persamaan (19.33) dan (19.33’)

didapat :

Faktor pembesaran = 2/1

1

/nfm

m

m

m x

kP

x

(19.36)

Faktor pembesaran digambarkan dalam bentuk grafik pada Gambar 19.9 terhadap sumbu

rasio frekuensi f /n sebagai berikut .

4

3

2

1

0

-1

-2

-3

321 n

f

kP

x

m

m

/

m

mx

atau

Gambar 19.9.

Terlihat bahwa jika f = n maka amplitudo getaran paksa menjadi tak terhingga.

Gaya luar atau gerakan penyangga berada pada kondisi resonansi dalam sistem getaran

tersebut. Secara aktual, amplitudo getaran tetap terhingga karena gaya redaman /

damping force (sub bab 19.9), bagaimanapun situasi tersebut harus dihindari dan

frekuensi paksa tidak boleh dipilih terlalu dekat dengan frekuensi naturalnya. Terlihat pula

untuk f < n maka koefisien sin f t pada persamaan (19.35) berharga positif, sedangkan

untuk f > n maka koefisien sin f t berharga negatif. Pada kondisi pertama, getaran

paksa disebut in phase (se-phase) dengan gaya luar atau gerakan penyanga, sedangkan

pada kondisi kedua, hal ini 180o out of phase (berbeda phase 180o).

Pada akhirnya kita dapat mengamati bahwa kecepatan dan percepatan getaran

kondisi stedi dapat diperoleh dengan mendefferensikan suku terakhir persamaan (19.35)

sebanyak 2 kali terhadap t. Harga maksimumnya tampil dalam bentuk yang serupa

dengan persamaan (19.15) di sub bab 19.2 kecuali bahwa rumusan tersebut melibatkan

amplitudo dan frekuensi putar getaran paksa, yaitu :

vm = xm f am = xm f 2 (19.37)

~ Getaran Mekanis ~


CONTOH SOAL 19.5.

Sebuah motor dengan massa 150 kg disangga oleh 4

pegas yang masing-masing memiliki konstanta 135

kN/m. Ketidak seimbangan rotor adalah ekuivalen

terhadap massa 30 gram yang diletakkan sejauh 150

mm dari sumbu rotasi. Jika diketahui bahwa motor

cenderung bergerak vertikal, tentukan :

a. kecepatan dalam rpm dimana resonansi terjadi

b. amplitudo getaran motor pada kecepatan 1200 rpm.

PENYELESAIAN :

a. Kecepatan resonansi.

Kecepatan resonansi sama dengan frekuensi putar natural n (dalam rpm) dari

getaran bebas motor. Massa motor dan konstanta pegas adalah :

m = 150 kg

k = 4 (135 kN/m) = 540 kN/m

kg

mN

m

kn

150

/540000 = 60 rad/det = 573 rpm

Kecepatan resonansi = 573 rpm

b. Amplitudo getaran pada 1200 rpm.

Kecepatan sudut motor dan massa yang tidak seimbang adalah :

= 1200 rpm = 125,7 rpm

m = 30 gram = 0,030 kg

Besar gaya sentrifugal terhadap ketidak seimbangan rotor adalah :

Pm = man = mr2 = (0,030 kg)(0,150 m)(125,7 rad/det)2 = 71,1 N

Defleksi statis yang disebabkan beban konstan Pm :

mkN

N

k

Pm

/540

1,71 = 132 m

Frekuensi gaya putar f dari gerakan adalah kecepatan sudut motor :

f = = 125,7 rad/det

Substitusi nilai Pm/k, f dan n ke persamaan (4) didapat :

22

60/7,1251

132

/1

/

nf

m

m

kPx

= -39 m

xm = 39 m (melebihi fase)

~ Getaran Mekanis ~


Catatan : Selama f > n maka getarannya 180o out of phase dengan gaya sentrifugal

akibat ketidakseimbangan rotor. Contoh, jika massa yang tidak seimbang secara

langsung berada di bawah sumbu rotasi maka posisi motor adalah xm = 39 m di atas

posisi seimbang.

tf

tP fm sin

Pm

m

~ Getaran Mekanis ~



~ Getaran Mekanis ~


SOAL – SOAL

15 kN/m30 kg

tPP fm sin

19.98. Balok 30 kg dipasang pada pegas dengan konstanta

k = 15 kN/m yang dapat bergerak tanpa gesekan dalam slot

vertikal sebagaimana tampak pada gambar di bawah ini.

Sistem ini bekerja akibat gaya periodik tPP fm sin

dimana f = 10 rad/s. Jika diketahui amplitudo gerak

adalah 18 mm, tentukan nilai Pm.

19.99. Sebuah slot 4 kg dapat bergeser tanpa gesekan pada batang horisontal dan

dipasang pada pegas dengan konstanta 450 N/m. Sistem ini digerakkan oleh gaya

periodik tPP fm sin dengan Pm = 13 N. Tentukan amplitudo gerakan slot jika (a)

diketahui f = 5 rad/s, (b) f = 10 rad/s.

~ Getaran Mekanis ~


GETARAN TEREDAM

*19.8. GETARAN BEBAS TEREDAM

Sistem getaran yang dipelajari pada bagian pertama bab ini diasumsikan tanpa

redaman. Sebenarnya semua getaran mengalami beberapa derajat redaman akibat gaya-

gaya gesek. Gaya-gaya ini dapat disebabkan oleh gesekan kering, atau gesekan

Coulomb, antara benda-benda kaku; oleh gesekan fluida jika benda kaku bergerak di

dalam fluida, atau oleh gesekan internal antara molekul-molekul benda elastis.

Satu tipe redaman khusus adalah viscous damping yang disebabkan oleh

gesekan fluida pada kecepatan rendah dan medium. Redaman viskos dicirikan oleh

kenyataan bahwa gaya gesek berbanding lurus dan berlawanan arah dengan kecepatan

gerak benda. Sebagai contoh, perhatikan sebuah benda bermassa m tergantung pada

pegas dengan konstanta k, diasumsikan bahwa benda terpasang pada plunyer dashpot

(gambar 19.10). Besar gaya gesek yang bekerja pada plunyer akibat fluida yang

melingkupinya sama dengan xc , dimana konstanta c dinyatakan dalam N.s/m atau lb.s/ft

dan disebut koefisien viscous damping, yang nilainya dipengaruhi oleh sifat-sifat fisik

fluida dan konstruksi dashpot.

Kesetimbanganx

W

xkT st

xmma

xc

Gambar 19.10.

Persamaan geraknya adalah : maF xmxcxkW st

0 kxxcxm 19-38)

Substitusikan x = e t dalam persamaan 19-38) kemudian bagilah dengan e t maka akan

diperoleh persamaan karakteristik :

m2 + c + k = 0 19-39)

dan diperoleh akar-akar persamaan :

~ Getaran Mekanis ~


m

k

m

c

m

c

2

22 19-40)

Didefinisikan koefisien redaman kritis cc sebagai nilai yang menyebabkan suku di bawah

akar pada persamaan 19-40) sama dengan nol, yaitu :

02

2

m

k

m

cc nc mm

kmc 22 19-41)

dimana n adalah frekuensi putar natural dari sistem tanpa redaman. Kita dapat memilah

3 jenis kasus redaman berdasarkan nilai koefisien c yaitu :

1. Heavy damping : c > cc; Akar persamaan karakteristik 19-39) 1 dan 2 adalah nyata

dan berbeda. Penyelesaian umum dari persamaan diferensial 19-38) adalah :

tteCeCx 21

21

19-42)

Penyelesaian ini berhubungan dengan gerakan tanpa getaran. Pada saat 1 dan 2

bernilai negatif kedua-duanya, x mendekati nol pada saat t meningkat tak terhingga.

Bagaimanapun pada kenyataannya sistem akan mencapai posisi keseimbangannya

setelah beberapa waktu tertentu.

2. Critical damping : c = cc; Persamaan karakteristik 19-39) memiliki akar ganda bernilai

= - cc / 2m. Penyelesaian umum untuk persamaan diferensial 19-38) adalah :

tnetCCx

)( 21 19-43)

Gerakan yang terjadi juga tanpa getaran. Sistem teredam kritis merupakan satu

bahasan khusus dalam rekayasa teknik untuk mendapatkan kondisi dimana sistem

dapat mencapai posisi keseimbangannya dalam waktu sesingkat mungkin tanpa

mengalami osilasi.

3. Light damping : c < cc; Akar-akar persamaan 19-39) merupakan bilangan kompleks

sekawan (conjugate complex). Penyelesaian umum untuk persamaan diferensial 19-

38) berbentuk :

)cossin( 21

)2/( tCtCex dd

tmc 19-44)

dimana d dirumuskan sebagai :

2

2

2

m

c

m

kd

Substitusikan 2/ nmk dan merujuk persamaan 19-41), diperoleh :

2

1

c

ndc

c 19-45)

~ Getaran Mekanis ~


Dalam hal ini konstanta c/cc dinamakan faktor damping. Meskipun gerakan yang

terjadi pada kenyataannya tidak bolak-balik sendiri, konstanta d umumnya dianggap

sebagai frekuensi putar getaran teredam. Dengan menggunakan metode substitusi

yang sama dengan sub bab 19.2 akan diperoleh penyelesaian umum persamaan 19-

38) dalam bentuk :

)sin()2/( texx d

tmc

o 19-46)

Gerakan yang didefinisikan oleh persamaan 19-46) adalah getaran dengan amplitudo

yang melemah (gambar 19.11) dan interval waktu d = 2 / d memisahkan dua titik

yang berurutan dimana kurva yang didefinisikan oleh persamaan 19-46) menyinggung

satu dari kurva pembatas sebagaimana tampak pada gambar 19.11, biasanya disebut

sebagai periode getaran teredam. Mengacu pada persamaan 19-45) terlihat bahwa d

< n sehingga d lebih besar dari periode getaran n dari sistem getaran tanpa

redaman yang bersesuaian.

x

x0

0

-x0

t1

x1

t2

x2

t3

x3

x4

t4

d

tmc

ex 2

0

t

Gambar 19.11.

~ Getaran Mekanis ~


*19.9. GETARAN PAKSA TEREDAM

Foto 19.2. Suspensi mobil sebagaimana tampak pada gambar secara esensial terdiri atas sebuah

pegas dan sebuah shock absorber yang akan menyebabkan bodi mobil mengalami getaran paksa teredam saat mobil dijalankan melalui jalanan tidak rata.

Jika sistem yang ditinjau pada sub bab sebelumnya dikenai gaya periodik P

dengan nilai P = Pm sin f t, persamaan gerak menjadi

tPkxxcxm fm sin 19-47)

Penyelesaian umum persamaan 19-47) diperoleh dengan menambahkan penyelesaian

partikular pada fungsi komplemen (penyelesaian umum) dari persamaan homogen 19-

38). Fungsi komplemen yang diberikan pada persamaan 19-42), 19-43) atau 19-44)

tergantung pada tipe damper yang digunakan. Persamaan tersebut mewakili gerak

transien yang selanjutnya teredam.

Perhatian utama pada sub bab ini adalah getaran steady state yang diwakili oleh

penyelesaian partikular persamaan 19-47) dalam bentuk

)sin( txx fmpart 19-48)

Substitusi xpart sebagai x pada persamaan 19-47), akan dihasilkan

tPtkxtxctxm fmfmfmffmf sin)sin()cos()sin(2

Dengan menyamakan tf berturut-turut dengan 0 dan /2, diperoleh

sinmmf Pxc 19-49)

cos)( 2

mmf Pxmk 19-50)

Kuadratkan kedua sisi persamaan 19-49) dan 19-50) kemudian dijumlah, diperoleh

22222 ])()[( mmff Pxcmk 19-51)

Dengan menyelesaikan persamaan 19-51) untuk xm dan membagi persamaan 19-49) dan

19-50) persuku akan diperoleh berturut-turut,

222 )()( ff

mm

cmk

Px

2tan

f

f

mk

c

19-52)

~ Getaran Mekanis ~


Mengacu pada persamaan 19-4) bahwa 2

nmk , dimana n adalah frekuensi putar

getaran bebas tidak teredam, dan dari persamaan 19-41) bahwa 2mn = cc, dimana cc

adalah koefisien damping kritis dari sistem, diperoleh

222 )]/)(/(2[])/(1[

1

nfcnfm

m

m

m

cc

x

kP

x

19-53)

2)/(1

)/)(/(2tan

nf

nfccc

19-54)

Persamaan 19-53) menyatakan faktor pembesaran dalam suku perbandingan

frekuensi (frequency ratio) nf / dan faktor damping c/cc. Ini dapat digunakan untuk

menentukan amplitudo getaran steady state yang dihasilkan oleh gaya dengan besaran P

= Pm sin f t atau akibat pergerakan landasan = m sin f t. Persamaan 19-54)

mendefinisikan sudut beda fase antara gaya paksa atau pergerakan landasan dengan

getaran steady state sistem teredam yang dihasilkan. Faktor pembesaran digambarkan

dalam grafik 19.12 untuk berbagai variasi nilai koefisien damping. Dapat dilihat bahwa

amplitudo getaran paksa dapat dijaga tetap kecil dengan memilih koefisien damper viskos

yang besar atau dengan memberikan perbedaan nilai yang besar untuk frekuensi natural

dan frekuensi getaran paksa.

Gambar 19.12.

~ Getaran Mekanis ~


*19.10. ANALOGI ELEKTRIK

Gerak bolak-balik sirkuit elektrik dinyatakan dalam persamaan diferensial yang

setipe dengan persamaan yang diperoleh pada sub bab sebelumnya. Karena itu

analisisnya mirip dengan sistem mekanis dan hasil yang diperoleh untuk sistem getaran

dapat digunakan untuk sirkuit yang ekuivalen. Sebaliknya, setiap hasil yang diperoleh

untuk sirkuit elektris juga dapat diaplikasikan untuk sistem mekanis yang bersesuaian.

Bayangkan satu sirkuit elektris yang terdiri atas satu induktor dengan induktansi L,

sebuah resistor dengan resistansi R dan kapasitor dengan kapasitansi C, yang

dihubungkan secara seri dengan sumber tegangan bolak-balik E = Em sin f t (gb. 19.13).

Dari teori sirkuit dasar dinyatakan bahwa jika i adalah arus yang mengalir dalam sirkuit

dan q menyatakan isian elektrik dalam kapasitor, penurunan potensial adalah L(di / dt)

pada induktor, Ri pada resistor dan q/C pada kapasitor. Jika dinyatakan bahwa jumlah

tegangan terpakai dan penurunan potensial pada loop sirkuit sama dengan nol, maka

0sin C

qRi

dt

diLtE fm 19-55)

Pengaturan ulang suku-suku persamaan dengan mengingat bahwa pada setiap kondisi i

sama dengan laju perubahan

GETARAN MEKANIS 19 - finahari.files.wordpress.com posisi – waktu tampak sebagai kurva sinus...

Documents

Transcript of GETARAN MEKANIS 19 - finahari.files.wordpress.com posisi – waktu tampak sebagai kurva sinus...