Spatial and temporal analysis of non-steady elongationof rice leavespce_2020 1..12

BORIS PARENT1, GENEVIEVE CONEJERO2 & FRANÇOIS TARDIEU1

1INRA, UMR759, Laboratoire d’Ecophysiologie des Plantes sous Stress Environnementaux, Place Viala, F-34060Montpellier, France and 2INRA, UMR5004 Biochimie et Physiologie Moléculaire des Plantes, Plate-forme d histocytologie etd imagerie cellulaire végétale TA A96/02, Cirad, av. Agropolis, 34398 Montpellier, France

ABSTRACT

A precise knowledge of the temporal and spatial distribu-tions of cell division and tissue expansion is essential forappropriate leaf sampling in omics studies and for analysesof plant–environment relations. Elongating leaves of ricewere studied during their whole development for elonga-tion rate, distribution of cell length, cell production rate andspatial distribution of growth in the leaf. In seven geno-types, the pattern of leaf elongation rate followed threephases: (1) an exponential increase before leaf appearance;(2) a short phase (2–4 d at 20 °C) with a stable leaf elonga-tion rate around leaf appearance; and (3) a phase of 8–10 dwith a progressive decrease in elongation rate. The profileof cell length along the leaf changed with time during thefirst and last phases, but was time invariant around appear-ance. We propose a method adapted to non-steady elonga-tion based on anatomical measurements, which wassuccessfully tested by comparing it with the prickingmethod. It allowed analysis of the change with time in thespatial distribution of growth from initiation to end of leafgrowth. The length of leaf zones with cell division and tissueelongation varied with time, with maximums of 21 and60 mm respectively around leaf appearance.

Key-words: cell expansion; development; division, leafgrowth; rice (Oriza sativa L.); spatial distribution.

INTRODUCTION

Leaf elongation rate is a major determinant of the final leafarea of monocotyledons at both individual and whole-plantscales (Bultynck et al. 2004; Reymond, Muller & Tardieu2004; Chenu et al. 2008). It has therefore a central role ingenetic and environmental variabilities of biomass accumu-lation and yield. In rice, leaf expansion is constrained by theextensibility of the epidermis (Kende & Kutschera 1989).Based on the development stage of epidermal cells, threeregions can be considered in the growing zone of mono-cotyledons, located in the first centimetres at the base of theleaf. The meristematic zone, located in the most proximalzone of the leaf, harbours both cell division and tissueexpansion of epidermal cells.A second zone located further

from the leaf insertion point harbours only tissueelongation. Cells originating from the meristematic zoneflow through the elongation-only zone, and finally reach themature zone where they get their final size (Boffey, Sellden& Leech 1980).The identification of the length of each zoneand of the spatial distributions of cell division and tissueexpansion allows analysis of environmental effects on themechanisms which govern leaf growth. In particular, theyguide the sampling for gene expression or protein contentsaimed at identification of molecular processes associatedwith growth (Vincent et al. 2005; Hachez et al. 2006; Mulleret al. 2007; Zhu et al. 2007).This information is not yet avail-able for rice, although rice becomes a model for other grassspecies (Genome 2005).

In monocotyledons, leaf growth is usually studied duringa steady-state period during which leaf elongation rate isconstant and the spatial distributions of leaf elongation rateand cell length are temporally invariable (Schnyder et al.1990; Ben Haj Salah & Tardieu 1995; Fiorani et al. 2000). Inthis case, anatomical methods to infer growth rate havebeen proposed by Gandar & Hall (1988) and Silk, Lord &Eckard (1989), while relationships between cell size, celldivision rate and growth in non-steady growth of grassleaves have been quantified by Gandar & Rasmussen(1991). In particular, the one-dimension continuity equa-tion (Silk & Erickson 1979; Gandar 1980) allows calculationof deposition rate of any compound, in particular of newcells (Silk & Erickson 1979; Silk 1992; Ben Haj Salah &Tardieu 1995; Maurice, Gastal & Durand 1997).

D zz

tv z

zz

zv z

z( ) = ∂ ( )

∂+ ( ) ∂ ( )

∂+ ( ) ∂ ( )

∂ρ ρ ρ (1)

where D(z) is the cell production rate per unit leaf length ata distance z from the leaf base, r(z) is the cell density perunit leaf length and v(z) is the local velocity. When thisequation is used during a period with a steady state, the

temporal factor∂ ( )

∂ρ z

tcan be discarded (Silk 1992).

The period with a steady state is short compared with theduration of leaf development (Durand, Schaufele & Gastal1999). In some species, such as maize or sorghum, most ofthe final leaf length still develops during this 1-week periodduring which the leaf elongation rate is much higher thanduring earlier periods (Muller, Reymond & Tardieu 2001).

Correspondence: F. Tardieu. Fax: +33 4 67 61 21 16; e-mail: tardieu@supagro.inra.fr

Plant, Cell and Environment (2009) doi: 10.1111/j.1365-3040.2009.02020.x

© 2009 Blackwell Publishing Ltd 1

In this case, concentrating analyses on the steady-stateperiod therefore accounts for most of the effects of envi-ronmental cues on cell division and expansion (Ben HajSalah & Tardieu, 1997, Granier, Turc & Tardieu 2000b;Rymen et al. 2007). It also allows simulation of the finalleaf length of all leaves of the plant (Chenu et al. 2008).However, the steady-state period is much shorter, if exist-ing, in other monocot species such as Festuca (Maurice et al.1997), and growth analysis should therefore be carried outduring the whole leaf development.

In this study, we have first checked whether the durationof the phase with a steady state was long enough in rice tobe self-sufficient for a growth analysis. Because resultsrevealed that this was not the case, we have analysed thetemporal and spatial patterns of leaf elongation and celldivision during the whole leaf development period beforeand after leaf appearance. We propose a method to calcu-late the spatial distribution of elongation rate, which applieswithout a steady state, based on the spatial distribution ofcell length in the growing zone. This method was tested bycomparing its outputs with the classical anatomical methodduring steady growth (Gandar & Rasmussen 1991; Beem-ster et al. 1996) and with the pricking method (Schnyder &Nelson 1989; Bernstein, Silk & Läuchli 1993; Ben Haj Salah& Tardieu, 1995), although the latter is difficult to use in ricebecause it causes a severe reduction in leaf elongation rate.This study therefore provides the first spatial analysis ofgrowth processes in the rice leaves, after solving method-ological difficulties associated to it, namely: (1) the absenceof a steady-state period; (2) the peculiar anatomy of the riceepidermis which obliged us to use a biphoton microscopeinstead of classic epidermal prints; and (3) the non-linearresponse of leaf elongation rate to temperature which ledus to use a temperature compensation of growth rates.

MATERIALS AND METHODS

Genetic material

Measurements were carried out on seven rice genotypes(Azucena, IR64, Nipponbare, Moroberekan, Vandana, Apoand CG14), belonging to two species, either Oryza glaber-rima (CG14) or Oryza sativa (all others). Three subfamiliesof O. sativa were considered, namely temperate japonica

(Nipponbare), tropical japonica (Azucena, Moroberekan)and indica (Apo, Vandana and IR64).

Plant culture

Greenhouse and growth chamber experiments were per-formed in the Phenodyn phenotyping platform (Sadok et al.2007). Plants were grown in PVC pots, 22 cm in diameterand 22 cm deep, containing a 50:50 (v/v) mixture of loamysoil (particle diameter ranging from 0.1 to 4 mm) andorganic compost. Columns were filled with 5 kg of soil,sampled for measurement of water content at filling time.Seeds (7 per pot) were sown at 1.5 cm depth. It was checkedthat soil water content was similar between columns andhomogeneous within each column.

Air temperature and relative humidity were measured atplant level every 30 s with two sensors per block in thegreenhouse (HMP35A, Vaisala Oy, Helsinki, Finland). Thetemperature of the meristematic zone was measured withfine copper–constantan thermocouples (0.2 mm diameter)inserted in the meristematic zones of more than 4 (non-measured) plants per treatment. Photosynthetic photon fluxdensity (PPFD) was measured every 30 s using two sensorsper block (LI-190SB, Li-Cor Quantum PAR, Lincoln,NE, USA or SOLEMS 01/012/012, Palaiseau, France). Allclimatic data were averaged and stored every 15 min in adata logger (Campbell Scientific, Wiring Panel, Shepshed,Leicestershire, UK). Soil water content was maintained at40% g/g of dry matter corresponding to a soil water poten-tial about -0.05 MPa, by daily watering with a modifiedone-tenth-strength Hoagland solution. Eight experimentswere carried out for genotype Azucena, three for genotypeIR64 and two for the other genotypes, in the greenhouseand in the growth chamber. The temperature was tightlycontrolled at 22 � 1 °C (day and night) in the growthchamber experiment 8 (Table 1). It fluctuated naturally inthe greenhouse with noontime temperatures of 28 � 3 °Cand night temperatures of 17 � 2 °C. One growth chamberexperiment also had fluctuating temperatures between dayand night.

Temperature compensation of time and rates

In order to unify experiments carried out in differentthermal scenarios, both time and rates were expressed as

Table 1. Summary of experiments carried out in this study

Experiment Lines PlaceTmin/Tmax

(°C)VPDmax

(kPa)PPFD(mmol m-2 s-1) Measured variables

1 Azucena, IR64 Greenhouse 17/31 2.8 750 LER before leaf appearance2 Seven lines Greenhouse 17/31 2.8 750 LER after leaf appearance3 Seven lines Growth chamber 15/28 2.8 550 LER after leaf appearance4–7 Azucena Greenhouse 15/30 2.8 700 LER after leaf appearance8 Azucena Growth chamber 22 2.2 550 Cell length and LER

Tmin and Tmax, minimum and maximum daily temperature during the experiment; VPDmax, maximum vapour pressure deficit; LER, leafelongation rate.

2 B. Parent et al.

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment

equivalent rates or time at 20 °C. The responses of leafelongation rate (LER) and of the reciprocal of the durationof the development of any leaf followed a commonresponse to temperature (T) in a companion study:

F TAT E

RTS

RH

RT( ) =

( )+ −( )

exp

exp

A

1 Δ Δ (2)

where A is a constant of proportionality, EA (kJ mol-1) hasthe units of an activation energy and R is the gas con-stant. The ratios EA/R, DS/R and DH/R were obtainedby curve fitting, EA = 85 kJ mol-1. DH = 348.6 kJ mol-1;DS = 1.14 kJ mol-1 K-1.

It follows that leaf elongation rate at any temperature,LER(T), can be transformed into an equivalent rate at20 °C, LER(20) by multiplying it by the temperature com-pensation ratio F(20)/F(T).

LER LER TFF T

2020( ) = ( ) ( )( )

(3)

LER LER TT

ER T

SR

HRT

20293 1

2931

1

1

( ) = ( ) − −( )⎡⎣⎢

⎤⎦⎥

+ −( )+

exp

exp

e

A

Δ Δ

xxp Δ ΔSR

HR−( )293

(4)

The reciprocal of the duration of leaf development fol-lowed a F(T) function which was common with that of leafelongation rate. It could therefore be temperature compen-sated by using Eqn 4. It follows that time can be expressedas equivalent time at 20 °C (t20°C).

t t TT E

R TS

RH

R

20293

1 1293

1 2931

( ) = ( ) − −( )⎡⎣⎢

⎤⎦⎥

+ −( )+

exp

exp

exp

A

Δ Δ

ΔΔ ΔSR

HRT−( )

(5)

Leaf length and elongation rate

Before the appearance of leaf 6, measurements of its elon-gation were based on destructive sampling.Twenty plants ofgenotypes Azucena and IR64 were dissected every dayfrom the appearance of leaf 5 until that of leaf 6 in thegreenhouse.The length of leaves 5–7 and of their blades andsheath were measured with a ruler. They were interpolatedwith exponential regression, so leaf elongation rate wasestimated by derivation of the resulting exponentialequation.

After leaf appearance, leaf elongation rate was continu-ously monitored with rotating displacement transducers(RDTs) (601–1045 Full 360 Smart Position Sensor; SpectrolElectronics, Ltd, Wiltshire, England), both in the green-house and in the growth chamber for the seven genotypesanalysed in this study. Leaf elongation was transmitted tothe sensor via a pulley attached to it, which carried a thread

attached to the leaf tip and to a 20 g counterweight. Mea-surements (every 15 min) began when the tip of the sixthleaf appeared above the whorl, and lasted until the end ofelongation. It led to thousands of data points (12 300 forAzucena, more than 2500 for other genotypes). Neithertemperature nor vapour pressure deficit (VPD) had aneffect on the thread extensibility (Sadok et al. 2007). Theeffect of counterweights on elongation rate was tested onAzucena genotype with counterweights of 10, 20, 30 g. Aneffect was observed during few hours after the beginning ofmeasurements, but no significant effect was observed after20 h. The first day of measurement was therefore discardedfrom the analysis.

Cell length and sampling procedure for spatialand temporal analysis of growth

Spatial analyses were carried out at 10 different timesduring the development of leaf 6 of genotype Azucena.Three to five plants were sampled in 10 d either before theappearance of leaf 6 (150, 100, 70 or 30 h20°C beforeappearance) or after it (20, 80, 120, 170, 190, 210 h20°C

after appearance). At each date, the lengths of leaves 5–7were measured. Leaf 6 was then cut into 3 mm long stripsfrom the leaf base to the tip. The samples were fixed inparaformaldehyde 2%, glutaraldehyde 2%, in 10 mm ofpotassium phosphate buffer (pH 7.2) overnight at 4 °C;dehydrated in ethanol series; and stored at 4 °C in ethanol70%. The same procedure was used in genotype IR64. Thesamples were then gently squeezed on a microscope slidein a mounting medium glycerol–PBS 80% just beforeobservation. Autofluorescence of cell walls or cell con-tents allowed visualizing and measuring epidermal cells inunstained preparations.

Images were obtained in the Montpellier PHIV Imag-ing platform with a multiphoton laser scanning Axiovert200M 510 META NLO Zeiss microscope (Carl ZeissMicroImaging, Jena, Germany). Excitation was providedby a mode-locked Ti–sapphire laser Chameleon Ultra II(Coherent, San Jose, CA, USA). We observed the sampleswith a lens C-Apochromat ¥40/1.2 water immersion Zeiss,and tested a range of near-infrared wavelengths from 700 to900 nm. A first procedure was used for very young tissues,with a wavelength of 720 nm (equivalent to 372 nm in clas-sical fluorescence microscope), a first dichroïc mirror HFTKP 700/488, a secondary dichroïc mirror NFT 490 and abandpass 435–485 IR filter. This procedure allowed us toidentify cells and count them.A second procedure was usedin tissues located at more than 25 mm from the leaf base,with a wavelength of 840 nm, a first dichroïc mirror HFTKP 700/488, a secondary dichroïc mirror NFT 545 anda bandpass 500–550 IR filter. This procedure allowedobserving the autofluorescence of cell walls. Images werethen analysed with the image analysis software (Bioscan-Optimas, version 4.10) to measure cell length.

Cell lengths were averaged for each sampling date (t) ateach distance from the leaf insertion point (z), in both thelamina and the sheath when the latter was long enough.

Non-steady elongation of rice leaves 3

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment

A Richard equation was fitted to the whole data set,separately in the lamina and the sheath.

l z la

k z z n( ) = ++ − −( )[ ]{ }( )0

011 exp

(6)

The parameters of this equation were determined foreach 10 h20°C time step during leaf development. Parametersk, n and l0 were kept constant for all sampling dates in orderto limit the number of parameters, in relation with thenumber of available data. Parameters a and z0 were fittedfor each sampling date. A cell length profile was then cal-culated for each sampling date, and the local cell densityr(z) was calculated as the reciprocal of l(z). The length ofthe elongation zone was determined from cell lengthprofile, as the zone which stopped where cells had reached95% of their final length.

Cell division rate

Mitotic figures were observed in each 3 mm long leaf strip,and the most distal mitosis was recorded for evaluating thelength of the division zone. The samples were incubated inDAPI 2 mm for 20 min and washed in water (5 min). Weused an excitation wavelength of 720 nm in the multiphotonmicroscope, with dichroïc mirror HFT KP 650 and bandpass435–485 nm IR filter. At each 10 h20°C time step during leafdevelopment, the total number of cells in blade and sheathwas calculated by integration of r(z) on the total length (L).

N z dzL

cell = ( )∫ ρ0

(7)

The cell production rate (P) was determined by temporalderivation of Ncell. This was done separately for sheath andblade. We have inferred the spatial distribution of cell divi-sion rate, RDRi(z) at each time (ti) and distance to leaf base(z) from the total cell production rate (Pi) and the length ofthe division zone (zD). Several patterns of the spatial distri-bution of cell division rate in the division zone were testedand compared for a sensitivity analysis. The first one wasthat described in Arabidopsis roots by Beemster & Baskin(1998) or in maize leaves by Granier, Inze & Tardieu(2000a). In these studies, RDR plateaued or slightlydecreased in a first zone, and rapidly decreased afterwardsuntil the end of the division zone. This pattern was fitted ona logistic curve.

RDR z ta

z z,

exp.

,i

i

i( ) =

+ − −( )⎡⎣⎢

⎤⎦⎥

12 5

0(8)

where ai and zi,0 are constant parameters at a given ti with ai,the value of cell division rate near the leaf insertion point,and zi,0 the parameter of the sigmoid.The parameter zi,0 wascalculated in such a way that the division rate in Eqn 8 was10% of its maximum value (ai) at the point with the lastobserved mitosis (zD), resulting in zi,0 = zD - 5.49 mm.

Equation 8 therefore depended only on parameter ai whichwas calculated at each sampling date in such a way that thecumulated cell division rate over the whole division zonewas equal to the cell production rate (Pi). Two otherpatterns were compared with that described here (seeResults).

Distribution of the relative elongation rate withthe pinhole method

The elongating zone of the leaf was marked with pinholesfor calculation of the displacement of the marks during a10 h period. Holes were pierced with fine pins (0.25 mmdiameter, Austerlitz insect pins, stainless steel, size 000)inserted through the sheaths of older leaves and thegrowing region of young leaves. Pins were longitudinallyaligned with the centre of the stem and were guided toensure a horizontal trajectory. The holes were spaced 4 mmapart for 100 mm. After 10 h, plants were excised; the sixthleaves were carefully freed from older, enclosing leaves; andfinal positions of pin marks were recorded. The elongationof segments between two neighbouring holes was obtainedby subtracting initial from final distances between holes.Leaf elongation rate of pierced plants was obtained bysumming elongations of all leaf segments. The effect ofpiercing injury was estimated as the ratio of the elongationof pierced plants to the mean elongation of non-piercedplants. Elongation of all segments was multiplied bythe reciprocal of this ratio. Relative elongation rate wascalculated as:

RERL L

L tLER

LER= −( )

−( )×Δ Δ

Δ Δi f i

i std

, ,

,

0

0

(9)

where DLi,0 and DLi,f are the initial and final distancesbetween holes i and i + l, LERstd is the mean elongation rateof non-injured plants and LER is the elongation rate of theconsidered plant.

RESULTS

The period with nearly constant leaf elongationrate was short, around leaf appearance

The elongation rate of leaf 6 was measured from theappearance of leaf 5, while leaf 6 was still hidden by olderleaves and was about 3 mm long, until the end of its elon-gation (Figs 1 & 2). The duration of this period differedbetween experiments if expressed in calendar time, but wascommon to all experiments in temperature-compensatedtime (equivalent time at 20 °C, h20°C). The period elapsingbetween the appearances of leaves 5 and 6 lasted 202 � 5and 231 � 10 h20°C in genotypes IR64 and Azucena, respec-tively, while the period between the appearance and the endof growth of leaf 6 lasted 290 and 350 h20°C in the same twogenotypes. In the same way, leaf elongation rate differedbetween experiments if expressed per clock time (e.g.4.2 mm h-1 in the greenhouse at 26 °C versus 2.7 mm h-1 in

4 B. Parent et al.

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment

the growth chamber at 22 °C just after the emergence ofleaf 6 of genotype Azucena). It was in a narrow range(2.25 � 0.15) if expressed per temperature-compensatedtime units.

During early development of leaf 6, its length andelongation rate increased exponentially and reached amaximum rate when the leaf emerged above the whorl(Fig. 1). After leaf appearance, leaf elongation ratedecreased slowly during the first 120 h20°C with a commonrate in six experiments carried out with genotype Azucena(Fig. 2a). It decreased more rapidly 120 h20°C after leaf emer-gence and nullified 350 h20°C after it in all experiments. Thesame slow decrease with time was observed in seven geno-types (Fig. 2b). A near-plateau of leaf elongation rate wasobserved for 2 d in genotypes CG14 and Moroberekan, butcould not be identified clearly in other genotypes. The totalduration of elongation after leaf appearance ranged from280 to 370 h20°C in the seven genotypes studied here.

The synchrony between the developments of leaves 5–7 ispresented in Fig. 3a. Leaf elongation rates of leaves 5 and 7decreased after their respective appearance, as did leaf 6.The rapid decrease in elongation rate of leaf 6 (100 h20°C

after leaf appearance onwards) occurred simultaneouslywith the beginning of rapid growth of leaf 7, while leaf 5stopped elongation. The sheath of leaf 6 began to grow atleaf emergence, elongated exponentially until 210 h20°C

after it while the blade elongation rate was decreasing. Thesheath stopped growing 350 h20°C after leaf emergence.

Overall, rice leaf elongation rate followed a pattern withthree marked phases (Fig. 3a): (1) one phase of exponential

150

200

50

100

50

100

Six

th leaf le

ngth

(m

m)

0

50

-200 -100 0

0–250 –200 –150 –100 –50 0

Time since appearance of sixth leaf (h20°C

)

Figure 1. Change with time in the length of leaf 6 before or justafter leaf appearance. The leaf emerges from older leaves at time0, taken as a reference in all figures of this study. Most of theperiod presented in this figure therefore corresponds to negativevalues. Time is expressed in equivalent hours at 20 °C. Mainpanel, genotype Azucena. Inset, genotype IR64. Closed triangles:leaf still enclosed in older leaves. Open circles: appeared leaf.Lines, exponential regression. Arrows indicate the appearance ofthe fifth leaf. Standard errors on parameters (when linearized)are lower than 5%; r2 > 0.9 in both genotypes.

3

1

2

0Azucena

IR64

Vandana

(a)

(b)

LE

R (

mm

h20°C

−1)

1

2 Moroberekan

Nipponbare

Apo

CG14

Time since appearance of sixth leaf (h20°C)

00 100 200 300

Figure 2. Change with time in leaf elongation rate (LER)of leaf 6 from leaf appearance (time 0) to the end of leafdevelopment in seven rice genotypes. Both time and rates areexpressed in equivalent hours at 20 °C. Periods with highevaporative demand (VPD > 1.5) were not kept in the analysisto avoid confusions of effects. (a) Box plots of changes with timeof LER in genotype Azucena. Data came from six differentexperiments in greenhouse and growth chamber (n = 40).(b) Change with time of LER in seven rice genotypes (n > 6in each line). Points are mean value every 10 h20°C. Confidenceintervals at 95% on mean values (not shown) were alwayssmaller than 0.2 mm h20°C

-1.

2.5(a)

0.5

1

1.5

2

Leaf 5Leaf 6

Leaf 7

(mm

h20°C

−1)

0

1

1.5

2Leaf

Blade

Sheath

Elo

ng

atio

n r

ate

(b)

0

0.5

−200 −100 0 100 200 300

Time from sixth leaf appearance (h20°C)

Figure 3. Time courses of elongation rate of the lamina, sheathor whole leaves 5–7 of genotype Azucena. Both rate and time areexpressed in equivalent hours at 20 °C. (a) Time courses of leafelongation rate (LER) of leaves 5–7. Before leaf appearance,lines are exponential regression curves. After appearance, datapoints are mean value every 10 h20°C time step calculated inleaves 5–7. Confidence intervals on LER values were lower than0.2 mm h20°C

-1. (b) Time courses of elongation rate of the sixthwhole leaf, blade and sheath. After 220 h20°C, the entire blade wasin the mature zone, so it did not elongate.

Non-steady elongation of rice leaves 5

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment

increase in rate which stopped at leaf appearance and coin-cided with the fastest growth rates of the older leaf 5; (2) ashort phase with a near-stable leaf elongation rate whichlasted 0–2 d depending on genotypes; and (3) a period of5–8 d with a progressive decrease in leaf elongation ratewhich coincided with the increase in elongation rate of theyounger leaf 7.

The time invariance of spatial distribution ofcell length was limited to a short period aroundleaf appearance

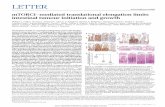
Epidermal cells of the adaxial face of the sixth leaf wereimaged with a multiphoton confocal microscope. The undu-lating aspect of the rice leaf epidermis (which mimickedvalleys parallel to the midrib, Fig. 4a) did not allow us to usethe classical method of leaf prints. The measured cells werein files without stomata located at mid-distance betweendumbbell-shaped cells on epidermal ridge over a vascularbundle (highest ‘altitudes’, small cells) and bulliform cells atlowest ‘altitudes’ (Fig. 4b).

At all sampling dates, cell length increased with the dis-tance to leaf base (Figs 4a & 5). Cells flew from the cell

division zone to the mature zone, while they increased inlength. At leaf 6 emergence, cell length increased from10.0 mm near the leaf insertion point to 61.2 mm at the endof the elongating zone in genotype IR64, and from 8.3 to65.8 mm in genotype Azucena (Figs 4c–e & 5a). At earlystages of leaf development, a gradient of cell length wasobserved from the base to the leaf tip (for instance at 150 or100 h before leaf appearance). Later on, cells stopped elon-gating at about 60 mm from the leaf insertion point so celllength presented a plateau at further distances.

Cells located at a given distance from the leaf insertionpoint changed in length during leaf development, exceptthose located in the basal 6 mm of the leaf which remained8. � 0.5 mm long (Fig. 5b,c). During early stages of leafdevelopment (from 150 to 70 h20°C before appearance ofleaf 6), cell length at a given position decreased with time,together with the gradient of cell length along the growthzone (Fig. 5b). Around leaf appearance (from 30 h20°C

before appearance until 80 h20°C after it), the spatial distri-bution of cell length became nearly stable with time(Fig. 5b,c). During the third phase of leaf development,while leaf elongation rate decreased with time, cell lengthincreased with time in the lamina at a given position in the

Figure 4. Confocal microscopy imagesof leaf 6 at appearance (genotypeAzucena). (a) Leaf section, transversal tothe leaf axis at 72 mm from the leaf base(mature zone). (b) Zoom correspondingto the white square in image (a). Arrowscorrespond to cell files used for spatialand temporal analyses of elongation.(c) Adaxial epidermis in leaf strip locatednear the insertion point (from 0 to 3 mmfrom the base). (d) Adaxial epidermis inthe leaf strip from 18 to 21 mm from thebase. (e) Adaxial epidermis in the leafstrip from 66 to 69 mm from the base,corresponding to the mature zone.(f) Mitotic figures in adaxial epidermis inthe leaf strip from 12 to 15 mm fromleaf base.

(a) (b)

200mm

50mm

20mm

20mm

(d)(c)

(e) (f)

50mm 20

mm

6 B. Parent et al.

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment

leaf. Cells of the sheath increased in size more rapidly thanthose in blade, leading to mature cells threefold longer inthe sheath than in the blade.

The zone with tissue elongation covered about the wholegrowing leaf until 70 h20°C before leaf appearance, andincreased in length until 30 h20°C before leaf emergence(Fig. 6). Its length was maximum from 30 h20°C before leafemergence to 80 h20°C after it, at 60 and 44 mm in genotypesAzucena (Fig. 6) and IR64, respectively. It decreased after-wards until the end of leaf development.

Cell production rate in the blade peaked at leafemergence and rapidly decreased afterwards

Cell production rate in one epidermal cell file (calculated asthe local slope of cell number, Fig. 7a) increased in the

80

(a)

20

40

60

IR64Azucena

0

40

60

t = −150 h20°C

t = −100 h20°C

(b)

0

20

60ell

length

(mm

)

t = −70 h20°C

t = −30 h20°C

t = 20 h20°C

(c)

20 h20°C

80 h20°C

120 h20°C

170 h20°C

190 h20°C20

40

60Ce

210 h20°C0

40

180Sheath

Blade

(d)

Distance to base (mm)

6040200 Top0

20

Figure 5. Spatial distribution of epidermal cell length and itschanges during leaf development. Time is expressed in equivalenthours at 20 °C. Points are mean values (n > 100) from fourdifferent plants. Error bars on x-axis are uncertainty on distanceto base because of the sampling of 3 mm length. Error bars ony-axis are confidence interval at 95% on mean length. They arevisible when they exceed the size of symbols. (a) Cell lengthprofiles in leaf of genotypes IR64 and Azucena at leafappearance. (b) Cell length profiles at four times before leafappearance (-150 h20°C, green points and line; -100 h20°C, deepblue points and line; -70 h20°C, orange points and line; -30 h20°C,light blue points and line) and just after leaf appearance (redpoints and line) in genotype Azucena. (c) Cell length profiles ofblade just after leaf appearance (red points and line) and at fivetimes after leaf appearance (80 h20°C, purple points and line;120 h20°C, green points and line; 170 h20°C, deep blue points andline; 190 h20°C, orange points and line; 210 h20°C, light blue pointsand line) in genotype Azucena. (d) Same data as in (c), with thelength of sheath cells (square points) shown.

80

100Mature zone

Elongation-only zone

0

20

40

60Division zone

0−200 −100 0 100 200

Time since leaf emergeance (h20°C)

Figure 6. Change with time of the lengths of zones of the leafwith cell division, with tissue elongation without division and ofmature zone in leaf 6 of genotype Azucena. Time is expressed inequivalent hours at 20 °C.

4000

6000

BladeSheath

(a)

30

0

2000

(b)

10

20

Time since leaf appearance (h20°C)

0−200 −100 0 100 200

Figure 7. Increase in cell number (a) and changes in cellproduction rate (b) in leaf 6 of genotype Azucena. Time isexpressed in equivalent hours at 20 °C. Open points, blade. Filledpoints, sheath.

Non-steady elongation of rice leaves 7

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment

blade until a maximal value (31.8 cell h20°C-1) around leaf

appearance. It decreased sharply after it and nullified atabout 210 h20°C (Fig. 7b). In the sheath, it increased to itsmaximal value at 120 h20°C after leaf appearance (4.8cell h20°C

-1) and decreased after it. During the early devel-opment of leaf 6, the zone with cell division covered thewhole leaf and increased with it (Fig. 6). At 100 h20°C beforeleaf 6 became apparent, the zone with cell division reacheda maximum length which did not change until 120 h20°C afterleaf appearance (21 � 2 mm). The length of the divisionzone during the same period was 14 mm in genotype IR64(not shown); 120 h20°C after leaf appearance, the zone withcell division decreased with time until the end of leaf devel-opment (Fig. 6).

Calculation of the spatial distribution ofelongation rate over the whole developmentalperiod of rice

As seen above, the spatial distribution of cell length can beconsidered as steady during the short period from 30 h20°C

before leaf emergence to 80 h20°C after it. In this case only,the equation of Gandar & Rasmussen (1991) can be used tocalculate the spatial distribution of the relative elongationrate, by derivating the velocity of displacement.

v z t LER t z t, ,i m i i( ) = ( ) ( )ρ ρ (10)

for each distance to leaf base (z) in the extension-only zone,at each time (ti) during the period with steady distributionof cell lengths, with r(z,ti) the local cell density (reciprocalof cell length), rm the cell density in the mature zone andv(z,ti) the velocity of displacement.

However, the above paragraphs show that one cannotrestrict the analysis of the spatial distribution of growth tothe period with a steady distribution of cell length, whichoccurred only 2–4 d around leaf emergence (for a develop-mental period of more than 14 d) and during which only35% of the total leaf length was established. The equationof Gandar and Rasmussen could therefore not be used, andthe temporal term of Eqn 1 was not considered as beingnull so the continuity equation was written as:

D z tz t

z tz t t

v z tz t

z tz

,,

,,

,,

,i

i

i

i

i

i

i( )( )

= ∂ ( )( )∂

+( )( )

∂ ( )∂

+ρ

ρρ ρ

ρ ∂∂ ( )∂

v z tz, i (11)

where D(z,ti) is the accumulation of new cells at time ti and

distance z. It follows thatD z t

z t,,

i

i

( )( )ρ

is the local division rate,

called RDRi(z).∂ ( )

∂v z t

z, i is the local relative expansion rate,

RERi(z) so Eqn 11 can be simplified as:

RER v z tz t

zRDR z

z tt

i ii

ii+ ( ) ∂ ( )[ ]

∂= ( ) − ∂ ( )[ ]

∂,

ln , ln ,ρ ρ(12)

We solved this equation at each ti as a first-order linear

differential equation of vi(z), with∂ ( )[ ]

∂ln ,ρ z t

zi named

bi(z) and RDR zz t

ti

i( ) − ∂ ( )[ ]∂{ }ln ,ρ

named ci(z):

v z b z v z c zi i i i′( ) + ( )⋅ ( ) = ( ) (13)

The solution of the differential equation was:

v z b x x A c x b x xz zz

i i i i i( ) = − ( )∂⎡⎣⎢

⎤⎦⎥

× + ( )⋅ ( )∂⎛⎝⎜

⎞⎠⎟∫ ∫∫exp exp

0 00

∂∂⎡⎣⎢

⎤⎦⎥

x

(14)

At z = 0 (leaf insertion point), vi is null because the firstmaterial point close to the leaf base does not move, so Ai isnull. It follows that

v z b x x c x b x x xz zz

i i i i( ) = − ( )∂⎡⎣⎢

⎤⎦⎥

× ( )⋅ ( )∂⎛⎝⎜

⎞⎠⎟

∂⎡∫ ∫∫exp exp0 00⎣⎣⎢

⎤⎦⎥

(15)

and the equation was simplified as:

v z RDR xx

tx

z

ii

i ii( ) = × ( ) − ∂ ( )( )

∂( )∂⎡⎣⎢

⎤⎦⎥∫1

0ρρ ρln

(16)

In the elongation-only zone, where mitosis have stopped,

ρi i iRDPR x x Pz

( )[ ]∂ =∫0

, with Pi the cell production rate

within the meristem. In case of steady spatial distribution

of cell length,∂ ( )[ ]

∂ln ρi z

tis null and Pi = rmLER(ti).

Equation 16 is therefore equivalent to that of Gandar &Rasmussen (1991), Eqn 10, in case of steady spatial distri-bution of cell length, and in the elongation-only zone, forexample, at leaf appearance in our data.

We have calculated the distribution of the relative elon-gation rate for the whole period in which cell lengths weremeasured and for the whole growing zone using Eqn 16.

The calculation of the temporal component∂ ( )[ ]

∂ln ρi z

twas

based on the change with time in cell density at any place ofthe elongating zone (Fig. 5). RDRi(z) was inferred from thelength of the division zone (Fig. 6) and on the total cellproduction rate cumulated over the whole division zone(calculated from the evolution of cell number with time, seeMaterials and Methods and Fig. 7). Three typical spatialdistributions of cell division rate were considered whichrespect the conditions of total flux and the length of thedivision zone. They had a low impact on the distribution ofrelative elongation rate (see below).

The resulting spatial distribution of the relative elonga-tion rate changed with time but kept a common patternduring leaf development (Fig. 8a,b). In the first region ofthe elongating zone, the relative elongation rate increasedslightly with distance to the leaf insertion point. In thefollowing zone, the relative elongation rate showed aclassical bell-shaped profile, reaching a maximum valuebetween 26 and 33 mm depending on the stage of develop-ment (0.072 h-1 at 33 mm from the base at leaf appearance).It increased with time in the whole elongation zone untilleaf appearance (Fig. 8a, maximum value from 0.009 to0.072 h-1). After leaf appearance, it decreased with time inthe whole elongation zone (Fig. 8b). The distance at whichthe relative elongation rate reached a maximum was nearly

8 B. Parent et al.

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment

stable before appearance (32 � 1.5 mm), and slightlydecreased afterwards. Note that during the period withconstant cell lengths (from -30 to 80 h20°C from leaf appear-ance), and in the elongation-only zone (z > 21 mm from leafbase), the results obtained with Eqn 16 are equal to thoseobtained with Eqn 10 (Gandar & Rasmussen 1991) becausethe two equations are strictly equivalent.

Check of the method during the nearsteady-state period: pinhole method andanalysis of the sensitivity of the distribution oflocal elongation rate to the profile of celldivision rate

The pinhole method was used during the period withhighest growth rate, during which it keeps a sufficientdegree of precision in spite of the reduction in elongationrate because of pricking injury (50–75%). When correctedby the ratio between the leaf elongation rates of non-injured and injured plants, the profile of relative elongationrate was similar to that inferred with the method developedin this study (Fig. 9a).

We have analysed the sensitivity of the profile of relativeelongation rate to the chosen shape of the profile of divisionrate (Fig. 9b–d). Three shapes found in the literature weretested. The first one, used earlier, corresponds to a plateaufollowed by a gradual decrease (Fig. 9b) as found in

Arabidopsis roots by Beemster & Baskin (1998) or in maizeleaves by Granier et al. (2000a). The second one is a bell-shaped curve (Fig. 9c) found in maize roots by Sacks et al.(1997) and maize leaves by Tardieu et al. (2000). The thirdone is a constant cell division rate (Fig. 9d) in the wholedivision zone, as discussed by Baskin (2000). The first twoshapes resulted in very similar profiles of relative elonga-tion rate. When the calculation was performed with anassumed constant cell division rate, the resulting relativeelongation rate increased exponentially with the distance tothe leaf base in the division zone, with a discontinuity at thejunction between the division zone and the elongation-onlyzone. Overall, the shape of the profile of cell divisionrate did not cause strong change in the profile of relative

0.06

0.08(a)

0

0.02

0.04

(b)

0.04

0.06

Distance to leaf base (mm)0 20 40 60 80

0

0.02

RE

R (h

20

°C−1

) −153 h20°C

−100 h20°C

−70 h20°C

−30 h20°C

20 h20°C

20 h20°C

80 h20°C

120 h20°C

170 h20°C

190 h20°C

210 h20°C

Figure 8. Profiles of relative elongation rate during leafdevelopment, leaf 6 of genotype Azucena. (a) Profiles at fourtimes before leaf appearance (-150 h20°C, green line; -100 h20°C,deep blue line; -70 h20°C, orange line; -30 h20°C, light blue line)and just after leaf appearance (red line). (b) Profiles just afterleaf appearance (red line) and at five times after leaf appearance(80 h20°C, purple line; 120 h20°C, green line; 170 h20°C, deep blueline; 190 h20°C, orange line; 210 h20°C, light blue line). Thick lines,sheath; thin lines, blade.

0.06

0.04

0.08RER

Anatomical method

Pinhole

(a)

0.06RDR

RER

0

0.02

Pinholemethod

(b)

0

0.02

0.04

RDR(c)

0

0.02

0.04

0.06RER

0

0.02

0.04

0.06RDR

RER

(d)

0 20 40 60 80

Distance to leaf base (mm)

RE

R (h

20

°C−1

)

Figure 9. Comparison of the profiles of relative elongation rate(RER) determined with the anatomical method presented hereand with the pinhole method (a) and sensitivity analysis of theprofile of RER to the assumed distribution of cell division rate(RDR) (b–d). (b) RDR assumed to follow a plateau with agradual decrease as found in Arabidopsis roots by Beemster &Baskin (1998) or in maize leaves by Granier et al. (2000a).(c) RDR assumed to follow a bell-shaped curve found in maizeroots and leaves by Sacks, Silk & Burman (1997) and Tardieuet al. (2000). (d) A constant cell division rate as discussed byBaskin (2000).

Non-steady elongation of rice leaves 9

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment

elongation rate, and no current direct measurement mayallow identification of the best hypothesis because differ-ences were too small.

DISCUSSION

Stable elongation rate and steady state inmonocotyledons: where is the rule and whereis the exception?

It is frequently stated that the leaf growth of monocoty-ledons comprises a long period with a constant leaf elon-gation rate and a steady state in the growing zone, asobserved in maize (Ben Haj Salah & Tardieu 1997; Rymenet al. 2007) and sorghum (Bernstein et al. 1993). The firstresult of this study was that the period with stable elon-gation rate was very short, if existing, in rice. This wasobserved over six experiments and seven genotypes, andcan therefore be considered as a characteristic of thespecies. Leaf elongation rate presented three markedphases, with an exponential increase before appearance,followed by a short phase with a near-stable leaf elonga-tion rate (about 2 d at 20 °C) and a long period with aprogressive decrease in leaf elongation rate. The patterndescribed here has similarities with other monocotyledonssuch as tall fescue (Maurice et al. 1997; Durand et al.1999), so it is legitimate to wonder where is the rule andwhere is the exception.

We propose that the pattern of leaf development issimilar in all the mentioned cases, with a difference in theduration of each phase. During the short period withsteady state around leaf emergence, the interplay of a con-stant cell division rate and of a stable pattern of growthresults in a temporally invariant spatial pattern of relativeexpansion rate, cell division rate and cell length, as alreadyobserved in Festuca or maize (Schnyder et al. 1990; BenHaj Salah & Tardieu 1995). The main difference betweenrice and better studied monocotyledons such as maize orsorghum is the duration of this steady-state period, whichresults in most of the final leaf length in maize (Mulleret al. 2001), but only a small part of it in rice or tall fescue.In our study, leaf elongation rate began to decrease whenthat of the following leaf began to increase rapidly,thereby supporting the theory of the self-regulatingdynamic system in which leaf growth depends on growthof other elongating leaves (Durand et al. 1999; Fournieret al. 2005).

Another apparent difference with other monocotyledonswas that cell length profiles were discontinuous with morethan threefold longer cells in the sheath than in the blade.This contrasted with observations on ray-grass (Schnyderet al. 1990) where spatial distribution of cell length was notaffected by the ligule. However, the profiles of relative elon-gation rate were not as discontinuous at the ligule site, inaccordance with observations on tall fescue (Maurice et al.1997), suggesting a common control of expansion and divi-sion in the sheath and in the blade, despite differences incell length.

The zones with cell division and tissueexpansion were unexpectedly long

The lengths of the zones with cell division and of tissueelongation were determined in two contrasting genotypes.Azucena is a tropical japonica-type genotype with longleaves, few tillers and high elongation rate, while IR64 isa semi-dwarf indica-type genotype with short leaves andlow elongation rate. These two genotypes represented theextremes of leaf growth rate and leaf length in the set ofseven genotypes which were analysed in Fig. 2b. It is there-fore likely that most genotypes of rice have a length ofgrowth zone which range between the values in IR64 andAzucena (44 and 60 mm, respectively). This length is sur-prisingly long compared to that previously described in theliterature (e.g. 6 mm, Lu & Neumann 1999), and to themean value of 30 mm described in other grass species(Bernstein et al. 1993; Beemster et al. 1996; Fiorani et al.2000; Arredondo & Schnyder 2003). It is closer thanexpected from the value in maize (Ben Haj Salah & Tardieu1995). In addition, the division zone covered one-third ofthe whole growing zone in both IR64 and Azucena, that is,much more than usually observed in poaceae (5–25%,Beemster et al. 1996; Fiorani et al. 2000; Bultynck et al.2003), but close to that observed in maize, (Ben Haj Salah &Tardieu 1995). A possible cause of these discrepancies maybe the choice of the studied leaf, older in our studies of riceand maize than that in other studies.The length of the zoneswith cell division and tissue expansion largely varied withdevelopmental stages, to the difference of the case in otherspecies (Muller et al. 2001, 2007). This is consistent withthose observed in Festuca and sorghum (Bernstein et al.1993; Durand et al. 1999). The shape of the profile of rela-tive elongation rate was not far from that observed in moststudies in which relative elongation rate follows a bell shape(Schnyder et al. 1990; Ben Haj Salah & Tardieu 1995;Maurice et al. 1997).

Validity of the method for spatial and temporalanalysis of growth

The method proposed here is a development of that pro-posed by Beemster et al. (1996) for cases in which no clearsteady state can be identified. Identification of the divisionzone and elongation zone during leaf development is anecessary condition for sampling procedures which takeinto account developmental pattern of the leaf (Vincentet al. 2005). Quantification of processes in each of thesezones is necessary for physiology-based approaches aimedat associating local elongation rate with transcript abun-dance, protein amounts or metabolite concentrations ascarried out in other species (Muller et al. 2007; Poroykoet al. 2007), or at calculating cell division rate (Sharp, Hsiao& Silk 1990; Maurice et al. 1997).

The spatial distribution of local elongation rate is classi-cally analysed either by measuring the temporal displace-ment of pinholes which physically mark the elongationzones every 4 mm (Fig. 9a, Schnyder et al. 1990; Ben Haj

10 B. Parent et al.

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment

Salah & Tardieu 1995; Maurice et al. 1997), or by combininginformation of the leaf elongation rate, the distribution ofcell length and the length of the division zone (Beemsteret al. 1996; Fiorani et al. 2000; Rymen et al. 2007). Neither ofthese methods was adequate in the present study. (1) Thepinhole method caused a drastic reduction in leaf elonga-tion rate in rice (50–75%), unlike the classical reductionby 30–50% observed in other species (Schnyder, Nelson &Coutts 1987; Ben Haj Salah & Tardieu 1995).We consideredthis method as a partial validation, which could only be usedwhen leaf elongation rate was large enough to ensure suf-ficient temporal and spatial definitions. (2) The methodbased on the spatial distribution of cell length is applicableto the case with a steady state, which was observed for avery short proportion of the leaf development period. Wehave therefore developed a method which uses the spatialdistributions observed at different times to infer the spatialdistribution of leaf elongation rate and its change with timeduring leaf development.

Accessing the profiles of relative elongation raterequired no further measurements than those in Fig. 7. It,however, has potential disadvantages which have to beweighted in further studies.The first one was that it is basedon a hypothesis on the shape of the profile of cell divisionrate. Our sensitivity analysis showed that this only margin-ally affected the spatial distribution of relative elongationrate. The second potential drawback is that the method isbased on a regression analysis of cell length. However, theequations used here are flexible and can be easily adaptedto other data set. Finally, the final equation (Eqn 16) cannotbe solved analytically to our knowledge, thereby requiringgood spatial and temporal definitions for the experimentalresults. In the data set presented here, the calculation of thespatial distribution of relative expansion rate finally provedto be robust in the sensitivity analysis, and provided dataconsistent with the pinhole method.

REFERENCES

Arredondo J.T. & Schnyder H. (2003) Components of leaf elonga-tion rate and their relationship to specific leaf area in contrastinggrasses. New Phytologist 158, 305–314.

Baskin T.I. (2000) On the constancy of cell division rate in the rootmeristem. Plant Molecular Biology 43, 545–554.

Beemster G.T.S. & Baskin T.I. (1998) Analysis of cell division andelongation underlying the developmental acceleration of rootgrowth in Arabidopsis thaliana. Plant Physiology 116, 1515–1526.

Beemster G.T.S., Masle J., Williamson R.E. & Farquhar G.D. (1996)Effects of soil resistance to root penetration on leaf expansion inwheat (Triticum aestivum L): kinematic analysis of leaf elonga-tion. Journal of Experimental Botany 47, 1663–1678.

Ben Haj Salah H. & Tardieu F. (1995) Temperature affects expan-sion rate of maize leaves without change in spatial-distributionof cell length – analysis of the coordination between cell-divisionand cell expansion. Plant Physiology 109, 861–870.

Ben Haj Salah H. & Tardieu F. (1997) Control of leaf expansionrate of droughted maize plants under fluctuating evaporativedemand – a superposition of hydraulic and chemical messages?Plant Physiology 114, 893–900.

Bernstein N., Silk W.K. & Läuchli A. (1993) Growth and develop-ment of sorghum leaves under conditions of NaCl stress. Planta191, 433–439.

Boffey S.A., Sellden G. & Leech R.M. (1980) Influence of cell ageon chlorophyll formation in light-grown and etiolated wheatseedlings. Plant Physiology 65, 680–684.

Bultynck L., Fiorani F., Van Volkenburgh E. & Lambers H. (2003)Epidermal cell division and cell elongation in two Aegilopsspecies with contrasting leaf elongation rates. Functional PlantBiology 30, 425–432.

Bultynck L., Ter Steege M.W., Schortemeyer M., Poot P. & LambersH. (2004) From individual leaf elongation to whole shoot leafarea expansion: a comparison of three Aegilops and two Triticumspecies. Annals of Botany 94, 99–108.

Chenu K., Chapman S.C., Hammer G.L., McLean G., Ben HajSalah H. & Tardieu F. (2008) Short-term responses of leafgrowth rate to water deficit scale up to whole-plant and croplevels: an integrated modelling approach in maize. Plant, Cell &Environment 31, 378–391.

Durand J.L., Schaufele R. & Gastal F. (1999) Grass leaf elongationrate as a function of developmental stage and temperature: mor-phological analysis and modelling. Annals of Botany 83, 577–588.

Fiorani F., Beemster G.T.S., Bultynck L. & Lambers H. (2000) Canmeristematic activity determine variation in leaf size and elon-gation rate among four Poa species? A kinematic study. PlantPhysiology 124, 845–856.

Fournier C., Durand J.L., Ljutovac S., Schäufele R., Gastal F. &Andrieu B. (2005) A functional–structural model of elongationof the grass leaf and its relationships with the phyllochron. NewPhytologist 166, 881–894.

Gandar P.W. (1980) The analysis of growth and cell production inroot apices. Botanical Gazette 141, 131–138.

Gandar P.W. & Hall A.J. (1988) Estimating position–time relation-ships in steady-state, one-dimensional growth zones. Planta 175,121–129.

Gandar P.W. & Rasmussen H. (1991) Growth-pattern and move-ment of epidermal-cells within leaves of Asphodelus tenuifoliusCav. Annals of Botany 68, 307–315.

Genome S.P.I.R. (2005) The map-based sequence of the ricegenome. Nature 436, 793–800.

Granier C., Inze D. & Tardieu F. (2000a) Spatial distribution of celldivision rate can be deduced from that of p34cdc2 kinase activityin maize leaves grown at contrasting temperatures and soil waterconditions. Plant Physiology 124, 1393–1402.

Granier C., Turc O. & Tardieu F. (2000b) Co-ordination of celldivision and tissue expansion in sunflower, tobacco, and pealeaves: dependence or independence of both processes? Journalof Plant Growth Regulation 19, 45–54.

Hachez C., Moshelion M., Zelazny E., Cavez D. & Chaumont F.(2006) Localization and quantification of plasma membraneaquaporin expression in maize primary root: a clue to under-standing their role as cellular plumbers. Plant Molecular Biology62, 305–323.

Kende H. & Kutschera U. (1989) The growth response in deepwa-ter rice: biophysical and ultra-structural investigations. PlantPhysiology 89 (Suppl. 4), 1–42.

Lu Z. & Neumann P.M. (1999) Water stress inhibits hydraulicconductance and leaf growth in rice seedlings but not the trans-port of water via mercury-sensitive water channels in the root.Plant Physiology 120, 143–152.

Maurice I., Gastal F. & Durand J.-L. (1997) Generation of form andassociated mass deposition during leaf development in grasses: akinematic approach for non-steady growth. Annals of Botany 80,673–683.

Muller B., Reymond M. & Tardieu F. (2001) The elongation rateat the base of a maize leaf shows an invariant pattern during

Non-steady elongation of rice leaves 11

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment

both the steady-state elongation and the establishment of theelongation zone. Journal of Experimental Botany 52, 1259–1268.

Muller B., Bourdais G., Reidy B., Bencivenni C., Massonneau A.,Condamine P., Rolland G., Conejero G., Rogowsky P. & TardieuF. (2007) Association of specific expansins with growth inmaize leaves is maintained under environmental, genetic, anddevelopmental sources of variation. Plant Physiology 143, 278–290.

Poroyko V., Spollen W., Hejlek L., Hernandez A., LeNoble M.,Davis G., Nguyen H., Springer G., Sharp R. & Bohnert H. (2007)Comparing regional transcript profiles from maize primary rootsunder well-watered and low water potential conditions. Journalof Experimental Botany 58, 279–289.

Reymond M., Muller B. & Tardieu F. (2004) Dealing with thegenotype ¥ environment interaction via a modelling approach: acomparison of QTLs of maize leaf length or width with QTLs ofmodel parameters. Journal of Experimental Botany 55, 2461–2472.

Rymen B., Fiorani F., Kartal F., Vandepoele K., Inze D. & BeemsterG.T.S. (2007) Cold nights impair leaf growth and cell cycle pro-gression in maize through transcriptional changes of cell cyclegenes. Plant Physiology 143, 1429–1438.

Sacks M.M., Silk W.K. & Burman P. (1997) Effect of water stress oncortical cell division rates within the apical meristem of primaryroots of maize. Plant Physiology 114, 519–527.

Sadok W., Naudin P., Boussuge B., Muller B., Welcker C. & TardieuF. (2007) Leaf growth rate per unit thermal time followsQTL-dependent daily patterns in hundreds of maize lines undernaturally fluctuating conditions. Plant, Cell & Environment 30,135–146.

Schnyder H. & Nelson C.J. (1989) Growth rates and assimilatepartitioning in the elongation zone of tall fescue leaf blades athigh and low irradiance. Plant Physiology 90, 1201–1206.

Schnyder H., Nelson C.J. & Coutts J.H. (1987) Assessment ofspatial distribution of growth in the elongation zone of grass leafblades. Plant Physiology 85, 290–293.

Schnyder H., Seo S., Rademacher I.F. & Kühbauch W. (1990)Spatial distribution of growth rates and of epidermal cell lengthsin the elongation zone during leaf development in Loliumperenne L. Planta 181, 423–431.

Sharp R.E., Hsiao T.C. & Silk W.K. (1990) Growth of the maizeprimary root at low water potentials: II. Role of growth anddeposition of hexose and potassium in osmotic adjustment. PlantPhysiology 93, 1337–1346.

Silk W. (1992) Steady form from changing cells. InternationalJournal of Plant Sciences 153, S49–S58.

Silk W.K. & Erickson R.O. (1979) Kinematics of plant-growth.Journal of Theoretical Biology 76, 481–501.

Silk W.K., Lord E.M. & Eckard K.J. (1989) Growth-patternsinferred from anatomical records – empirical tests using longi-sections of roots of Zea mays L. Plant Physiology 90, 708–713.

Tardieu F., Reymond M., Hamard P., Granier C. & Muller B. (2000)Spatial distributions of expansion rate, cell division rate and cellsize in maize leaves: a synthesis of the effects of soil water status,evaporative demand and temperature. Journal of ExperimentalBotany 51, 1505–1514.

Vincent D., Lapierre C., Pollet B., Cornic G., Negroni L. & Zivy M.(2005) Water deficits affect caffeate O-methyltransferase, ligni-fication, and related enzymes in maize leaves.A proteomic inves-tigation. Plant Physiology 137, 949–960.

Zhu J., Alvarez S., Marsh E.L., et al. (2007) Cell wall proteome inthe maize primary root elongation zone. II. Region-specificchanges in water soluble and lightly ionically bound proteinsunder water deficit. Plant Physiology 145, 1533–1548.

Received 2 April 2009; received in revised form 1 July 2009; acceptedfor publication 2 July 2009

12 B. Parent et al.

© 2009 Blackwell Publishing Ltd, Plant, Cell and Environment