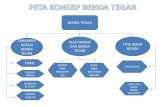
Gerak Benda Tegar(1)
-
Upload
marizal-kuswandi -
Category
Documents
-
view
195 -
download
7
description
Transcript of Gerak Benda Tegar(1)

Gerak Benda Tegar
Kelompok 71. Riya Astini (106)
2. Eri Dwi Prasetyo (013)

Benda tegar adalah sistem benda yang terdiri dari sistem-sistem benda titik yang tak hingga banyaknya dan jika ada benda yang bekerja padanya jarak antara titik anggota sistem selalu tetap. Jadi perbedaan antara benda titik dan benda tegar adalah adanya perubahan jarak pada sistem benda titik yang mengalami gaya.
Definisi

Pada gambar 9-1a, adalah sistem benda titik, karena 2 titik dihubungkan dengan pegas yang jarak 2 titik tersebut dapat berubah-ubah jika padanya bekerja gaya.
Pada gambar 9-1b adalah benda tegar karena keduanya dihubungkan dengan tongkat yang dapat berubah panjang jika gaya bekerja padanya.

Gambar 9-2 menunjukkan bahwa untuk pusat massa yang diam,gerak relatif benda (1) terhadap benda (2) yang mungkin terjadi adalah gerak rotasi.
Gerak Relatif yang sederhana adalah memilih pusat massa sebagai pusat sistem koordinat, sedangkan gerak relatif yang mungkin terjadi dalam gerak benda tegar dan sistem koordinat pusat massa adalah rotasi terhadap pusat massa dalam keadaan diam.

Gerak Benda Tegar terdiri dari:
a) Gerak Pusat Massa, yaitu bila lintasan semua titik tersebut sejajar, disebut translasi.
b) Rotasi terhadap Pusat Massa yaitu bila lintasan semua titik dari benda tersebut berbentuk lingkaran yang pusatnya pada sumbu putar yang melalui pusat massa.

1. Gerak Rotasi Murni (gbr a)Pusat massa diam dan benda-benda bergerak mengelilingi pusat massa.
2. Gerak Translasi Murni (gbr b)Pusat massa bergerak, sedangkan benda-benda tidak berubah terhadap pusat massa atau diam.
3. Gerak Rotasi dan Translasi bersama-sama (gbr c)Pusat massa bergerak, benda-benda juga berotasi terhadap pusat massa.
Macam-macam Gerak benda Tegar

Gerak Menggelinding
1. Menggelinding pada Bidang DatarJika silinder bergulir tanpa selip, maka silinder tersebut bergerak secara translasi dan rotasi. Pada kedua macam gerak tersebut berlaku persamaan-persamaan berikut.
Untuk gerak translasi berlaku persamaanF – f = m a dan N – m g = 0
Untuk gerak rotasi berlaku persamaanτ= I x α
Karena silinder bergulir tanpa selip, maka harus ada gaya gesekan.

Karena silinder bergulir tanpa selip, maka harus ada gaya gesekan.Besarnya gaya gesekan pada sistem ini adalah sebagai berikut
Jika disubstitusikan ke dalam persamaan F – f = m a, maka persamaanya menjadi seperti berikut

Gerak translasi diperoleh dengan mengasumsikan semua gaya luarbekerja di pusat massa silinder. Menurut hukum Newton:a. Persamaan gerak dalam arah normal adalah N – mg cos Θ = 0.b. Persamaan gerak sepanjang bidang miring adalah mg sin Θ – f = ma.c. Gerak rotasi terhadap pusat massanya τ= I x α .
Gaya normal N dan gaya berat mg tidak dapat menimbulkan rotasiterhadap titik O. Hal ini disebabkan garis kerja gaya melalui titik O, sehingga lengan momennya sama dengan nol. Persamaan yang berlaku adalah sebagai berikut.
2. Menggelinding pada Bidang Miring

sedangkan untuk rumus kecepatan benda di dasar bidang miring setelah menggelinding adalah sebagai berikut.

Benda-benda yang berotasi terhadap suatu titik yang tetap (sumbu putar) berarti setiap titik pada benda tersebut akan melakukan gerak melingkar dengan pusat lingkarannya berada pada sumbu putar. Di sini terdapat persamaan antara besaran-besaran dan translasi yaitu :1. Besaran sudut putar yang dibuat oleh suatu benda,
sebanding dengan pergeseran x.2. Kecepatan putar (sudut) , sebanding dengan kecepatan v.3. Percepatan putar (sudut) , sebanding dengan percepatan a.
Hubungan antara besaran-besaran translasi dan rotasi adalahS = r VT = r aT = r
dengan r adalah jarak titik ke sumbu putar.
Kinematika Rotasi

Besaran Kinematis Rotasi terdiri dari : = sudut putar, = kecepatan putar dan = percepatan putar. Rumus-rumus kinematika rotasi sebanding dengan rumus-rumus kinematika translasi yaitu: = o + ot + ½ t2
= o + t
Besaran-besaran Kinematis Rotasi
dt
d
t
dt
d
t
t
t
0
0
lim
limDengan Definisi

1. Gerak Melingkar Beraturan = konstan atau = 0
2. Gerak Melingkar Berubah Beraturan 0, < 0, berarti gerak melingkar dipercepat atau diperlambat.
Macam-macam Gerak Rotasi

Bila Kecepatan sudut gerak melingkar adalah , maka:
v = wrYang hubungannya secara vektoris dinyatakan :
Kecepatan Dan Percepatan


1. Sebuah rotor dipercepat dari diam menjadi berputar 20.000 rpm dalam waktu 5 menit. a.Berapa percepatan sudut rata-ratanya?b.Berapa banyak putaran dibuat rotor untuk mencapai
kecepatan ini?ω = 20.000 putaran/menit =20.000 = 2095,24 rad/s
ω = ω0 + αt
2095,24 = 0+ α 5. 60
α = 6,98 rad/s2
θ = ω0t + 1/2 αt2 = 0+ ½. 6,98. (5. 60)2
= 314.285,71 rad = = 50.045 putaran
Contoh Soal !
271,285.314
ikdet60rad2

2. Sebuah roda gila (grindstone wheel) berputar dengan percepatan konstan sebesar 0,35 rad/s2. Roda ini mulai berputar dari keadaan diam (o = 0) dan sudut mula-mulanya o = 0.Berapa sudut dan kecepatan sudutnya pada saat t=18 s ?
Jawab :
putaranrad
tt
o
o
932007,56
)18)(35,0(2
1)18(0
2
1
2
2
sputaranssrad
srad
t
o
o
/1/360/3,6
/3,6)18)(35,0(0
radian2360putaran1 o

3. Dalam suatu analisis mesin helikopter diperoleh informasi bahwa kecepatan rotornya berubah dari 320 rpm menjadi 225 rpm dalam waktu 1,5 menit ketika mesinnya dihentikan.
a). Berapa percepatan sudut rata-ratanya ?b). Berapa lama baling-balingnya berhenti ?c). Berapa kali baling-balingnya berputar sampai berhenti ?
Jawab :
putaranc
menittb
sputarant
a
o
o
809)3,63(2
3200
2).
1,53,63
3200).
/3,635,1
320225).
222
2

4. Sebuah bola pejal bermassa 10 kg berjari-jari 70 cm menggelinding di atas bidang datar karena dikenai gaya 14 N. Tentukan momen inersia,percepatan tangensial tepi bola, percepatan sudut bola, gaya gesekan antara bola dan bidang datar, serta besarnya torsi yang memutar bola!

5.Sepeda motor balap mula-mula diam. Setelah start, 10 sekon kemudian kecepatan rodanya menjadi 36 putaran persekon.a. Hitungkah percepatan sudut roda sepeda motorb. Hitunglah jumlah putaran roda selama 10 sekon Penyelesaian:
Diketahui:Δ t = 10 sekonΔ ω = 36 putaran/sekon
Soal: a. = ... ?
b. θ = .... ? Jawab:
a. = =
= 3,6.2 = 7,2 rad/s2
= 3,6 put/s2
b. θt = θ0 + t2
= 0 +1/2 . 7,2 102
= 1/2. 720 = 360 rad= 180 putaran

The End.....
Thank you....

1. Sebuah rada roda gila memerlukan waktu 3 sekon untuk berputar melalui 234 rad.Pada akhir waktu ini kecepatan sudutnya 108 rad/s.Hitunglah percepatan sudut konstannya???
2. Berapa lama waktu yang diperlukan sebuah roda dari keadaan diam sampai roda mencapai kecepatan 88,4 rad/s jika percepatan sudutnya sebesar 8,5 rad/s² ??
3. Sebuah benda berputar pada suatu sumbu dengan perpindahan sudut yang besarnya dinyatakan dalam persamaan θ = 8t2 – 5t + 3 (θ dalam radian dan t dalam sekon). Tentukan:a. Tentukan perpindahan sudut saat t = 0 dan t = 3 sekonb. Tentukan kecepatan sudut saat t = 0 dan t = 3 sekon
4. Kecepatan sudut benda pada saat t=0 ialah 4rad/s,dan percepatan sudutnya konstan dan sama dengan 2rad/s².Garis OP benda itu ketika t=0 dalam keadaan horizontal.
a. Berapa besar sudut yang diperlukan garis ini pada saat t=3s. b. Berapa kecepatan sudut pada saat ini.5. Partikel bergerak rotasi dengan α = (4t + 7) rad / s2.
Tentukan Percepatan rata-rata dari t = 0 hingga t = 2 sekon
Soal Latihan