Modeling of the HESCO nozzle diffuser used in IEA Annex-20 experiment test room

Available online at www.sciencedirect.com

Building and Environment 39 (2004) 367–384

www.elsevier.com/locate/buildenv

Modeling of the HESCO nozzle di)user used in IEA Annex-20experiment test room

S. Luo∗, B. RouxLaboratoire de Mod�elisation et Simulation Num�erique en M�ecanique (L3M) L3M-IMT, Technopole de Chateau-Gombert,

Marseilles Cedex 20 13451, France

Received 21 May 2003; received in revised form 18 September 2003; accepted 26 September 2003

Abstract

The modeling of air supply devices has been identi6ed from the IEA (International Energy Agency) Annex-20 project as one of themost important problems in applying computational 8uid dynamics to predict air 8ow pattern and air distribution in buildings. In thispaper, a simpli6ed model for the modeling of the HESCO nozzle di)user used in the IEA Annex-20 test room is tested and evaluatedagainst experimental data. It is found that with the ReNormalization Group k–� turbulence model and local mesh re6nement, this modelcan give very good prediction of the wall jet 8ow issued from the di)user. The in8uences of di)erent numerical discretization schemes andturbulence models for the prediction of the wall jet 8ow are also investigated. Flow asymmetry phenomena observed both in numericalsimulations and in experiments are discussed.? 2003 Elsevier Ltd. All rights reserved.

Keywords: CFD; Air supply di)user; Ventilation; Wall jet; Flow asymmetry; Local mesh re6nement

1. Introduction

Since the pioneering work of numerical simulation of ven-tilation 8ow by Nielsen [1], computational 8uid dynamics(CFD) has gained widespread application in analyzing in-door air 8ow and heat and mass transfer in buildings in thelast two decades. It is now becoming one of the most use-ful tools for predicting air 8ow pattern and air distributioninside buildings. CFD prediction can provide detailed infor-mation on air 8ow velocity, turbulence intensity, tempera-ture and contaminant distributions etc. in rooms which isin general very diBcult and time consuming to obtain withscale-model or full-scale 6eld experiments and at the sametime very important for the evaluation of indoor air qual-ity (IAQ) and thermal comfort. CFD is also a cost-e)ectiveway to conduct a parameter study or a trade-o) study fordi)erent ventilation con6gurations in the early design stage,for innovative ventilation system design and for ventilationsystem optimization. When appropriately used, CFD can bea very powerful design tool, but it has not yet developedto the stage that it can be used as a foolproof design tool;

∗ Corresponding author.

much e)ort and expertise are required to appropriately con-duct a simulation of practical ventilation 8ows, and also theresults must be validated against experimental data and thepredicted results judged with engineering insight.A lot of work has been done in an e)ort to turn CFD

into a design tool for the prediction of practical ventilation8ows, for example, the evaluation study of turbulence mod-els for simulating ventilation 8ows by Chen [2,3] and Gan[23], the scale-model study and comparison with numericalsimulation of Murakami et al. [5] and Nielsen et al. [6,7],the di)user modeling studies of Nielsen [8,9] and Chen etal. [10], to cite a few. Among them the most importantand noteworthy might be the large international researchproject IEA Annex-20, Air Flow Pattern in Buildings, or-ganized by the International Energy Agency (IEA). Twomain aims of its subtask-1 Room Air and Contaminant Floware: (a) to evaluate the performance of 3D complex andsimpli6ed air 8ow models in predicting air 8ow patterns,energy transport and indoor air quality inside buildingsand in their applicability as design tools and (b) to acquireexperimental data for the evaluation and validation of nu-merical models [11]. In this project, extensive full-scale3D experiments on forced convection, mixed convectionand natural convection as well as related numerical simu-lations have been carried out by di)erent research groups,

0360-1323/$ - see front matter ? 2003 Elsevier Ltd. All rights reserved.doi:10.1016/j.buildenv.2003.09.013

368 S. Luo, B. Roux / Building and Environment 39 (2004) 367–384

and the performance of modeling methods and numericalmodels were evaluated against experimental data. One im-portant output from this project is that it was identi6ed thatthere are two important problems which greatly hamperthe CFD application in numerical simulation of ventilation8ows, i.e., the modeling of turbulence and the modelingof air supply devices [11]. Turbulence exists in almostall the ventilation 8ows, for the sake of thermal comfortand energy saving, ventilation 8ows are often controlledso that the maximum velocity in the occupied zone isless than 0:2 m=s; thus ventilation 8ow is often not fullydeveloped turbulent 8ow with signi6cant low-Reynoldsnumber e)ects, which poses special diBculty for the con-ventional turbulence models to handle because almost allthe turbulence models were developed and calibrated fromsome simple high-Reynolds number 8ows. The commonlyused wall-function approach to bridge the fully devel-oped turbulent 8ow region with the viscosity-in8uencednear-wall 8ow region is not appropriate when pervasivelow-Reynolds number e)ects exist in the 8ow domainwhich is often the case in ventilated space [12]. The airsupply devices provide the main driving force (momentum)of air motion in the rooms, thus the air 8ow pattern insidethe rooms is often dictated by the characteristics of the airsupply devices—this is especially true for mixing ventila-tion systems. Therefore the correct modeling of air supplydevices is of vital importance for the correct prediction ofroom air8ow and heat and mass transfer in rooms [8,10].In IEA Annex-20 project, for evaluating the capability of

CFD as a design tool for practical ventilation 8ows, a com-plicated HESCO-type nozzle di)user was purposely cho-sen as the air supply device with the intention of testinghow such a complicated air supply di)user which is repre-sentative of modern air supply devices can be modeled innumerical simulations and what are the consequences of dif-ferent modeling approaches [8]. It was found that the mod-eling of such a di)user is particularly diBcult [10,11]. TheHESCO nozzle di)user used in IEA Annex-20 experimentswas comprised of 84 small round nozzles arranged in 4 rowson a rectangular plate of 0:71 m×0:17 m size (Fig. 1a). Allthe round nozzles have an equal diameter of 11:8 mm, eachnozzle can be adjusted independently to a di)erent directionand in all the IEA Annex-20 experiments, all the nozzleswere adjusted to 40◦ angle upward (Fig. 1b).

The di)user was installed at the horizontal center of oneof the side walls and a little below the ceiling of the testroom (Fig. 4). In the vicinity of the di)user, the supplied air6rst forms 84 small round jets and then after a rapid mix-ing, the small jets soon merge into a single jet which thenimpinges at an oblique angle on the ceiling and developsinto an attached 3D wall jet. Experiment showed that thedecay of the maximum jet velocity is very fast due to theintensive mixing of the small jets. At a ventilation rate of 3ACH (air change per hour), the maximum jet velocity dropsto 1:5 m=s at approximately 0:1 m in front of the di)user,where the small jets already merge into a large one (Fig. 2).

Fig. 1. The HESCO nozzle di)user used in the IEA Annex-20 project[10]. (a) HESCO nozzle di)user; (b) orientation of the nozzles.

Fig. 2. Smoke visualization of the wall jet 8ow at the symmetry planeof the test room at 3ACH [13].

The conventional turbulence models have diBculty to cor-rectly handle the multi-jet mixing and the oblique 3D jet im-pingement. Also the complicated internal structure and thelarge-scale di)erence between the di)user and the test roompreclude a full resolution of the di)user in the numerical sim-ulation, because that would necessitate a prohibitively largenumber of mesh grids in the jet region which would thendemand too large a computational resource to carry out thenumerical simulation. One objective of the IEA Annex-20project is to evaluate the capability of simpli6ed air 8owmodels in predicting indoor air8ow patterns [8,11]. Thus inthe IEA Annex-20 framework, several simpli6ed models forthe nozzle di)user have been proposed and tested in the nu-merical simulations. For the purpose of evaluating di)erentmodeling approaches, the wall jet pro6les issued from the

S. Luo, B. Roux / Building and Environment 39 (2004) 367–384 369

Fig. 3. Momentum modeling at the air supply devices [8]. (a) Basicmodel, (b) 12 slots model, (c) 84 slots model, (d) momentum model.

di)user were measured in a full-scale experiment test roomby Ewert et al. [14] and Heikkinen [13]. Fontaine et al. [4]carried out also a 1

6 water scale model experiment to studythe 8ow characteristics of the HESCO nozzle di)user. Thesimpli6ed models tested in the IEA Annex-20 project canbe divided into two groups (after Chen et al. [10]):

• Momentum modeling at the air supply devices: in thisapproach, the initial jet momentum of the di)user is im-posed directly at the supply opening as the boundarycondition for the supply di)users,

• Momentum modeling in front of the air supply di)users:in this approach, the momentum at some distance down-stream of the di)user is used as the boundary conditionfor the supply di)user.

In the IEA Annex-20 project, the models tested in the 6rstgroup include simple rectangular slot model and momen-tum model; in the second group, box model and prescribedvelocity model [11].In the simple rectangular slot model, three variants—the

basic model, the wide-slot model and the multiple slotsmodel—were tested (Fig. 3a–c). The basic model representsthe supply di)user as a single rectangular opening with thesame e)ective 8ow area and aspect ratio as the real di)userwhich is located at the center of the di)user. It was foundthat this model can reasonably predict the room air8ow pat-terns, but the jet pro6les and decay are not well predictedbecause it predicts a di)user with a very small jet area thus

Fig. 4. Con6guration of the di)user test room [10]. (a) Con6guration ofthe test room. (b) Location of the inlet di)user and the exhaust opening.

limits the spreading of the jet. Another study showed thatthis model is not suitable for non-isothermal air8ow simula-tions [10]. For this reason, a wide-slot model which is alsoa single rectangular opening with the same e)ective 8owarea but much bigger aspect ratio (width/height) than thereal di)user was tested. Heikkinen [13] showed that with thewide-slot model, the mixing in the core region and the jetpenetration were over-predicted. A multiple slots model inwhich the di)user was represented as 12 or 84 rectangularslots was also tested (Fig. 3b, c), it can give somewhat bet-ter prediction than the single slot models but the predictedresult is still not satisfactory compared with the experimen-tal data. The momentum model was originally developed byChen et al. [10] in which the di)user is represented as anopening with the same size of the real di)user which canbe regarded as evenly distributed in6nite jets (Fig. 3d). Toensure the correct mass and momentum 8ows from the dif-fuser, the mass 8ow and momentum 8ow are decoupled andspeci6ed separately at the supply opening.The box model was 6rst developed by Nielsen [1] and has

been successfully used by Nielsen et al. [6] in a numericalsimulation of a 2D ventilation 8ow. In this model, the dif-fuser boundary condition is speci6ed on an imaginary boxsurface around the di)user (Fig. 4) and the 8ow 6eld insidethe box is ignored. Appropriate jet formulae can be used tospecify the velocity pro6les at the surface in front of the dif-fuser, or measured data can be used. On the other surfaces,a free boundary with zero gradients in the normal directionof the surfaces for 8ow parameters (velocity, temperature,concentration, etc.) is speci6ed. Good agreement with ex-perimental data was reported by Nielsen [9] when using the


box model, but in the study of Heikkinen [13], it was foundthat the box model overpredicts the maximum jet velocitymore than other simpli6ed models. The problem associatedwith the box model is how to determine the box size. If thejet formulae are to be used for providing the jet pro6les onthe box surfaces, the box should be large enough to ensurethat the boundaries are in the fully developed jet region be-cause only in that region the velocity and temperature pro-6les are self-similar. At the same time, the box should besmall enough to avoid the impact of room air circulation andthermal plumes on the jet [10]. A practical problem is thatin most cases, it is not known where the fully developed jetregion begins. Like the box model, the prescribed velocitymodel prescribes the velocity pro6les of the jet on a planeat some distance downstream the di)user which can be ob-tained from jet formulae or from the measurements. Unlikethe box model, the 8ow in the volume between the di)userand the plane is included in the calculation domain and iscontinuously updated as the calculation progresses. At thesupply opening, the boundary conditions can be speci6edusing the basic model.In the hydraulic water scale model study of Fontaine

et al. [4], the box model was used to simulate the 8ow pat-tern in the scale model room. When using measured veloc-ity pro6les as the boundary condition for the box model, theresult was not satisfactory. They supposed the problem maycome from the measurement because in their hydraulic testbench, it is very diBcult to get reliable results very closeto the ceiling using laser doppler anemometer (LDA). Theythen used the jet formulae determined by Skovgaard et al.[15] to specify the boundary condition on the box surfaces,and a good correlation between the predicted and measuredvelocity pro6les at di)erent places in the model room wasobtained. The model they used is, in reality the prescribedvelocity model because the box volume was included in thecalculation domain. At the supply opening, an averaged nor-mal velocity was speci6ed so that the 8ow rate at the inletwas equal to that of the experiment.Emvin et al. [16] compared the basic model, the momen-

tum model, the box model and a full resolution method ofthe nozzle di)user in a numerical study. He concluded thatthe full resolution of the nozzle di)user is precise but needstoo many mesh grids near the di)user and the best choicemay be the box model if measured experimental data areavailable. Through a simple analysis, he concluded that themomentum model is not self-consistent and should not beused in numerical simulations. His analysis was based onthe free jet assumption (momentum conservation) which isnot valid for the HESCO nozzle di)user: not only the jetmomentum is not conserved because of the mixing of thesmall jets [10], but also the jet impinged on the ceiling anddeveloped into an attached wall jet. On the other hand, thestudy of Heikkinen [13] showed that the momentum modelperforms better than the basic and wide-slot models and thusit was recommended that this model can be used more gen-erally. Chen et al. [10] showed that the prediction of Emvin

et al. [16] by a full resolution method did not even repro-duce qualitatively the correct jet-8ow pattern observed withsmoke visualization. He concluded that the full resolutionmethod may not be a reliable design tool even though theassociated computational e)ort is signi6cantly increased.In a recent ASHRAE report, Chen et al. [10] reviewed

di)erent simpli6ed models for some widely used air supplydi)users. They concluded that the momentum model in the6rst group and the box model in the second group are themost promising models for the modeling of air supply dif-fusers. In their own numerical simulation, the performancesof the momentum model and the box model for the HESCOnozzle di)user were compared. They found that the momen-tum model cannot predict the small recirculation 8ow be-tween the di)user and the ceiling on the upper left corner ofthe room—which was veri6ed by smoke visualization of thejet 8ow as shown in Fig. 2—while the box model can pre-dict it. In their box model, measured velocity pro6les wereapplied at two surfaces of a “tiny-box”: the surface beforethe di)user and the top surface of the box. With the RNGk–� turbulence model, they observed that the maximum jetvelocity at the jet center plane (symmetry plane of the testroom) was overpredicted approximately 25% for velocitypro6les at two di)erent sections of the test room, i.e., at 1and 2:2 m distance in front of the di)user. They then arti-6cially decreased the supply velocity by 25% on the twotiny box surfaces and the predicted maximum jet velocityagrees well with experimental measurement. They then con-cluded that the tiny box model is the best model for thiskind of di)user. In practice, their tiny-box model requiresthe supply of measured velocity pro6les at the box surfaceswhich is often not feasible. Even with the measured veloc-ity pro6les, the correct prediction still needs a calibrationwith measured jet pro6les which are, in general, not readilyavailable, and it is not known whether the calibration factor(−25%) is Reynolds-number dependent because the cali-bration was done against only one ventilation rate (3ACH).Also the size of the “tiny box” was determined by compari-son with experimental data but was not determined a priori.Thus this model is more of an ad hoc model than a generalone, and signi6cant e)orts are needed to specify the mea-sured data on the box surfaces as the boundary conditions.A more general and easy-to-use model for this kind of dif-fuser is highly desirable for wider applications of numericalsimulation of ventilation 8ows.Because the jet 8ows issued from the small nozzles were

oriented upward at a 40◦ angle, the 8ow in the vicinity ofthe di)user is not aligned with any of the three coordinatedirections which can increase the numerical di)usion in nu-merical simulations. A high-order numerical discretizationscheme or a “local mesh re6nement” is needed to achieve abetter resolution of the jet 8ow especially in the vicinity ofthe di)user. The aim of the present study is to re-evaluatethe possibility of better prediction of the jet 8ow by a simpli-6ed model for the di)user—the momentum model togetherwith local mesh re6nement and/or higher-order numerical


discretization scheme. The performances of di)erent turbu-lence models for the prediction of the wall jet 8ow will alsobe tested and compared. We especially focus on the evalu-ation of the performance of the RNG k–� turbulence modelbecause it has been recommended by several authors for thesimulation of ventilation 8ows [2,17–19,23].

2. Experimental setup

In the IEA Annex-20 project, Ewert et al. [14] measuredthe velocity pro6les in the wall jet 8ow issued from theHESCO nozzle di)user in an experiment test room with di-mensions of 4:8 m×3 m×2:5 m (length×width×height).The air supply di)user is located at the horizontal cen-ter of a rear wall and 0:2 m below the ceiling of the testroom; the exhaust device is located on the same wall and1:4 m above the 8oor and it is of the size of 0:2 m × 0:3 m(height × width) (Fig. 4). Measurements were carried outusing LDA at X = 1 m in front of the supply di)user andat three vertical sections: Z = 0 m (symmetry plane of theroom), Z=0:25 m and Z=0:5 m and at Y =2:1–2:5 m, thevelocity 8uctuations (turbulent kinetic energy, TKE) in thethree coordinate directions were also measured.Heikkinen [13] measured the jet velocity pro6les at

X = 2:2 m on the symmetry plane of the room usingomni-directional anemometers under the same test condi-tion. The ventilation rate for these tests was 3ACH.

3. Modeling and numerical simulation

The time-averaged Navier–Stokes equations are solvedusing the commercial 8ow solver FLUENT 6, based on the6nite-volume method. The in8uence of the turbulent mo-tions on the mean 8ow is represented by a two-equation k–�or k–! turbulence model or by a second-moment Reynoldsstress model (RSM).

3.1. Turbulence models

Three k–� type turbulence models, i.e. the standard k–�model, the RNG k–� model and the realizable k–� modeland two k–! type turbulence models, i.e. the standard k–!model and the shear-stress-transport (SST) k–! model aretested. A second-moment RSM model mainly based on theproposals of Gibson et al. [20] and Launder et al. [21] witha wall-re8ection term in the pressure-strain model is alsotested. To bridge the main 8ow and the viscosity-a)ectednear-wall 8ow in the room, the enhanced near-wall treat-ment which is a near-wall modeling method that combinesa two-layer model with enhanced wall function is used. Theenhanced wall function is a smooth blending of the laminarlaw-of-the-wall and the logarithmic law-of-the-wall, whichextends its applicability throughout the whole near wall re-

gion, i.e., laminar sublayer, bu)er region, and fully devel-oped turbulent outer region [22].For the prediction of 2D ventilation 8ows, Chen [2] com-

pared the performance of 6ve k–� turbulence models—thestandard k–� model, the low-Reynolds number (LRN) k–�model of Lam-Bremhorst, the two-layer k–� model of Rodi,the two-scale k–� model of Kim and Chen and the RNG k–�model—in predicting natural convection, forced convectionand mixed convection 8ows in rooms, as well as impingingjet 8ow. He found that the prediction for the mean velocity ismore accurate than for the turbulent velocity. All these mod-els are not able to predict anisotropic turbulence correctlyor to pick up the secondary recirculation of indoor air 8owbut among them the RNG k–� model gives the best overallprediction results and was recommended for indoor air8owsimulations. According to the recommendation of Chen [2],Buchanan [17] and Loomans [19] adopted the RNG k–�turbulence model in their numerical study of 3D indoor air8ows and a good correlation of the predicted results withexperimental data was found using this model. In a detailedparameter study of the RNG k–� model, Gan [23]also recommended the use of this model to predictbuoyancy-induced air 8ows in rooms. Djunaedy et al. [18]found that the RNG k–� model yields better results than thestandard k–� model in a numerical simulation of a four-wayceiling air supply di)user. Thus in this study, although theperformances of the above mentioned two-equation turbu-lence models and the RSM model for the prediction of thewall jet 8ow are tested, the focus is on the evaluation of theperformance of the RNG k–� turbulence model.

3.2. Boundary conditions and numerical schemes

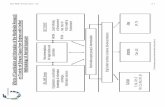
3.2.1. Inlet di8userThe momentum model is used to model the nozzle dif-

fuser. The momentum 8ow provided by the di)user is spec-i6ed as a momentum source added to a volume (the 6rstgrid layer) adjacent to the di)user (Fig. 8) and is calculatedfrom the mass 8ow rate and the e)ective 8ow area of thedi)user. At the supply opening, the total mass 8ow rate andthe 8ow direction are speci6ed.

3.2.2. Exhaust openingAt the exhaust opening, a Dirichlet condition for the pres-

sure is speci6ed, i.e., the gauge pressure at the outlet is set aszero. The Neumann condition for the pressure is also testedand no di)erence is found between the predicted results withthese two methods. Because there are often reversed 8ows atthe exhaust opening at the initial iteration stage, the Dirich-let condition o)ers better stability and convergence in thiscase [22] and thus the Dirichlet condition is preferred.

3.2.3. Turbulence quantitiesAccording to Skovgaard et al. [15] and Lemaire [11],

the inlet turbulence intensity is assumed to be 10% and the


boundary conditions for k and � when using k–� modelsand RSMmodel are calculated using the following formulae[15]:

kinlet = 1:5I 2U 2inlet ;

�inlet = C3=4 k3=2inlet=l;

where, I is the turbulence intensity, l is the length scale of thedi)user, l=0:07 D [22,24] and D is the hydraulic diameterof the di)user, which is calculated using the e)ective 8owarea of the di)user at 3ACH (≈ 0:00855 m2 [15]).At the exhaust opening, the turbulence intensity of the

reversed 8ow is assumed to be 1%.Alternate methods for specifying the turbulence quanti-

ties available in FLUENT such as turbulence intensity andhydraulic diameter etc. are also tested and no essential dif-ference is found between the results from these di)erentmethods. Further tests with higher turbulence intensities of15% and 20% are also carried out; no signi6cant in8uenceis found for the predicted results. This is in accordance withthe results reported by Awbi [25] and Jourbert et al. [10].For the k–! models, a turbulence intensity of 10% and

the hydraulic diameter of the inlet opening are speci6ed todetermine the boundary condition for k and !.

3.2.4. Discretization schemesThe discretization scheme for all the convection terms is

the second-order upwind or the QUICK scheme, and forthe di)usion terms, the second-order central-di)erencingscheme is used. For the discretization of pressure, thePRESTO! (PREssure STaggering Option) scheme is used.The SIMPLEC (SIMPLE-Consistent) scheme is used forthe pressure–velocity coupling for the steady-state sim-ulation and the PISO (pressure-implicit with splitting ofoperators) scheme is used for the time-dependent simu-lation. The time-marching scheme in the time-dependentsimulation is 6rst-order implicit.

3.3. Comparison of predicted jet pro=les withexperimental data

Most of the simulations are carried out with two-equationk–� and k–! turbulence models and also a second-momentRSM model in a half-room con6guration. Some simula-tions are carried out in a full-room con6guration to inves-tigate the 8ow asymmetry problem. The predicted jet 8owpro6les (velocity, TKE) at X = 1:0 and 2:2 m are com-pared with the experimental data of Ewert et al. [14] andHeikkinen [13].After some initial tests, two meshes, 60 × 55 × 34 for

half-room con6guration and 60 × 55 × 68 for full-roomcon6guration, are chosen as the main computation meshes.The mesh is more condense in the near wall regions andnear the di)user, where more steep velocity gradient is ex-pected. A typical computation mesh (60× 55× 34, Mesh1)for half-room con6guration is shown in Fig. 5. In Figs. 6

and 7, the predicted velocity pro6les and turbulent kineticenergy pro6les in the wall jet 8ow from the mesh grid60× 55× 34 using the RNG k–� turbulence model and themomentum model for the di)user are compared with thosefrom 6ner meshes of 68×61×38 (Mesh2) and 80×61×38(Mesh3) for the half-room con6guration. It can be seen fromFigs. 6 and 7 that the predicted velocity and turbulent ki-netic energy pro6les of the wall jet 8ow from these threemeshes are nearly the same, except at the side section ofZ = 0:25 m, where the 6ner meshes yield a slightly betterprediction for the velocity pro6le. The maximum jet veloc-ity at the jet center line is underpredicted at X = 1 m butoverpredicted at X = 2:2 m (Fig. 6). The turbulent kineticenergy pro6les are seriously underpredicted especially at thesection of Z = 0:5 m—this has been investigated in IEAAnnex-20 project when using standard k–� turbulence model[11] and has also been reported by Chen et al. [10] whenusing RNG k–� turbulence model and the box model for thedi)user.In Figs. 6 and 7, the predicted velocity pro6les and tur-

bulent kinetic energy pro6les using local mesh re6nementfrom the 60 × 55 × 34 mesh (Mesh1) are also shown. Itcan be seen that with local mesh re6nement, signi6cantimprovement for the prediction of both the velocity pro-6les and turbulent kinetic energy pro6les can be achieved.Excellent agreement of the predicted velocity pro6les withexperimental measurements is obtained at the jet centerplane. At the two side sections of Z = 0:25 and 0:5 m, theagreement of predicted velocity pro6les with those of theexperiment is reasonable too. The agreement of the pre-dicted turbulent kinetic energy pro6les with experimentalmeasurements is less satisfactory, but the general trendsare well predicted. Table 1 gives a quantitative comparisonof the predicted maximum velocity and turbulent kineticenergy in the wall jet 8ow with the respective measuredvalues.The local mesh re6nement is achieved using the Region

Adaptation Utility in FLUENT. Each grid cell before thedi)user from X =0 to 0:3 m, Y =2:13 to 2:5 m and Z=0 to0:355 m is halved in each coordinate direction. Thus eachcell is divided into 8 cells, which increases the total meshgrid size from 112,200 to 135,720 cells (Mesh1+LR1 (localre6ne1) in Figs. 6 and 7). Mesh1+LR2 (local re6ne2) isdone by repeating the process on the locally re6ned mesh(Mesh1 + LR1), except that the re6nement range in the Xdirection is from X = 0 to 0:25 m. The result obtained withthis latter mesh is slightly better than with its parent mesh(Mesh1+LR1), but the total number of cells is more thandoubled (from 135,720 to 302,978 cells). The total gain isvery little compared with the increased computational cost.Thus in the following simulations, the computation meshused is Mesh1+LR1.Fig. 8 describes how the mesh is locally re6ned

(Mesh1+LR1). It shows also the region where themomentum source is added (the 6rst grid layer adjacent tothe di)user). It is found essential that the local mesh


Fig. 5. The computation mesh for the jet 8ow of the IEA HESCO di)user.

Fig. 6. Comparison of the calculated velocity and turbulent kinetic energy pro6les with experimental data at the jet center plane (Z =0 m, X =1 m and2:2 m).

re6nement range in the streamwise direction, i.e., the Xdirection, should at least cover the impinging region (i.e.,x¿ 0:2=tanh 40◦ ≈ 0:24 m). When the re6nement range inthe X direction is less than 0:25 m, the improvement forthe prediction is greatly reduced.

Chen et al. [10] reported that with the momentum modelfor the supply di)user and a grid resolution of 50× 32× 35(also in half-room con6guration), the recirculation 8ow atthe upper left corner of the test room as shown in Fig. 2 can-not be predicted by the RNG k–� model. They repeated their


Fig. 7. Comparison of the calculated velocity and turbulent kinetic energy pro6les with experimental data at two planes parallel to the symmetry plane(X = 1 m and Z = 0:25 m, 0:5 m).

Fig. 8. Description of the local mesh re6nement (Mesh1+LR1). (a) X = 0 m Plane (Inlet wall), (b) Z = 0 Plane (Symmetry plane).


Table 1Quantitative comparison of the predicted maximum velocity and turbulence kinetic energy at di)erent sections of the wall jet 8ow with experimental dataa

Mesh 1 Mesh 2 Mesh 3 Mesh 1+LR1 Mesh 1+LR2(60× 55× 34) (66× 61× 38) (80× 61× 38)

X = 1 m Vel. Vmax (m/s) 0.99 0.974 0.99 1.083 1.073 1.078Z = 0 m Error (%) −8.2 −9.6 −9.6 +0.46 −0.46

Y position (m) 2.48 2.483 2.482 2.483 2.483 2.48TKE kmax (m2=s2) 0.056 0.056 0.056 0.058 0.0605 0.08187

Error (%) −31.6 −31.6 −31.6 −29.2 −26.1Y position (m) 2.4 2.4 2.4 2.4 2.4 2.4

X = 1 m Vel. Vmax (m/s) 0.546 0.611 0.587 0.665 0.67 0.8Z = 0:25 m Error (%) −31.8 −23.6 −26.6 −16.9 −16.3



X = 1 m Vel. Vmax (m/s) 0.201 0.189 0.221 0.471 0.462 0.467Z = 0:5 m Error (%) −57 −60 −52.7 +0.86 −1.07



X = 2:2 m Vel. Vmax (m/s) 0.725 0.743 0.742 0.666 0.714 0.69Z = 0 m Error (%) +5.1 +7.7 +7.7 −3.5 +3.4

Y position (m) 2.467 2.469 2.469 2.476 2.475 2.46

aThe “+” and the “−” signs indicate over- and under-prediction, respectively.

Fig. 9. Comparison of the predicted 8ow 6elds at the upper left corner on the symmetry plane of the test room with RNG k–� model and with/withoutlocal mesh re6nement. (a) Grid resolution 60× 55× 34 (Mesh1), (b) Mesh 1 + LR1.

simulation with 6ner meshes, but still failed to predict therecirculation 8ow. In the present simulation using the RNGk–� model and a grid resolution of 60× 55× 34, the recir-culation 8ow cannot be predicted. However when the meshgrids at the proximity of the di)user are locally re6ned, therecirculation 8ow can be well predicted, although the sizeof the recirculation zone is slightly smaller than that foundexperimentally by smoke visualization (about 0:2 m×0:2 m[10]). Fig. 9 is a comparison of the calculated 8ow 6eldsat the upper left corner on the symmetry plane of the testroom obtained with the RNG k–� model and with/without

local mesh re6nement. It is also observed that as the gridresolution near the supply di)user is increased, the size ofthe predicted recirculation zone at the upper left corner ap-proaches more and more the measured size.

3.4. In>uence of the pressure-gradient correction term inthe enhanced wall treatment

In the enhanced near-wall treatment in FLUENT, an op-tion accounting for the pressure-gradient e)ect is included.With this option, it is found that the prediction for the wall


Velocity (m/s)

Ro

om

Hei

gh

t (m

)

0 0.2 0.4 0.6 0.8 1 1.22

2.1

2.2

2.3

2.4

2.5

X=1m, Z=0mTestE2(Step5540)TestE2(Step6182)TestE2(Step8440)TestE2(Step14604)TestE2(Step15740)Ewert et al. (1991)

Velocity (m/s)

0 0.15 0.3 0.45 0.6 0.75 0.92

2.1

2.2

2.3

2.4

2.5

X=2.2m, Z=0mTestE2(Step5540)TestE2(Step6182)TestE2(Step8440)TestE2(Step14604)TestE2(Step15740)Heikkinen (1991)

Velocity (m/s)

Ro

om

Hei

gh

t (m

)

0 0.15 0.3 0.45 0.6 0.75 0.92

2.1

2.2

2.3

2.4

2.5

X=1m, Z=0.25mTestE2(Step5540)TestE2(Step6182)TestE2(Step8440)TestE2(Step14604)TestE2(Step15740)Ewert et al. (1991)

Velocity (m/s)

0 0.1 0.2 0.3 0.4 0.5 0.62

2.1

2.2

2.3

2.4

2.5

X=1m, Z=0.5mTestE2(Step5540)TestE2(Step6182)TestE2(Step8440)TestE2(Step14604)TestE2(Step15740)Ewert et al. (1991)

Fig. 10. Comparison of calculated velocity pro6les with experimental data at di)erent iteration stages (mesh size: 60 × 55 × 34, with local meshre6nement: X = 0 ∼ 1:5 m, Y = 2:13 ∼ 2:5 m, Z = 0 ∼ 0:355 m).

jet 8ow can be improved; it is especially bene6cial for theprediction of the turbulent kinetic energy pro6les. The im-provement may come from the fact that this term accountsfor some e)ect of the sudden change of pressure at the jetimpinging region.

3.5. E8ect of di8erent discretization schemes for theconvection terms

The QUICK discretization scheme for convection termsis also tested. The predicted results degraded greatly ascompared with those obtained with second-order upwindscheme, and it is found that the calculation with the QUICKscheme is more diBcult to converge, a result also observedby Chen et al. [10].

3.6. Flow asymmetry in the test room

When the geometrical con6guration is symmetric, a sym-metric 8ow condition is often assumed in order to save com-

puting time, but it is not always valid. There is experimentalevidence to the contrary in some cases. In an experimentalstudy, Zhang et al. [26] has reported asymmetric 8ow in asymmetric test room meant to produce 2D 8ow pattern whenthere is no any obvious disturbance. Fontaine et al. [4] ob-served asymmetric 8ow behavior both in their water scalemodel experiment and in their numerical simulations for theIEA Annex-20 nozzle di)user. This phenomenon was alsoobserved in the full-scale experiments in IEA Annex-20 TestRoom by di)erent research groups [11].In the present study, when the symmetry boundary con-

dition is imposed at the symmetry plane (half-room con6g-uration), the computed 8ow pattern does not reach a steadysolution even after many thousands of iterations. At a certainiteration step, the residuals no longer decrease but oscillateirregularly at an acceptable level. It is observed that when-ever there is an oscillation peak in the residuals, it is accom-panied by a change of 8ow pattern, and the solution is timedependent with some irregular periodicity. Fig. 10 showsa comparison of the predicted velocity pro6les with


Fig. 11. Predicted velocity contours near the ceiling (Y = 2:48 m) at di)erent iteration stages (mesh size: 60 × 55 × 34, with local mesh re6nement:X = 0 ∼ 1:5 m, Y = 2:13 ∼ 2:5 m, Z = 0 ∼ 0:355 m).

experimental data at di)erent iteration stages. It can beseen that the predicted velocity pro6les near the di)user (atX =1 m and Z=0 m, 0:25 m) are greatly in8uenced by thechange of 8ow pattern, but at X =2:2 m and Z =0:5 m thein8uences are much smaller. The predicted turbulent kineticenergy pro6les show similar trends. In Fig. 11, an exampleof the predicted velocity contours just under the room ceil-ing (Y = 2:48 m) at di)erent iteration stages is shown. Itcan be seen that at the iteration steps 8440 and 15,740, thepredicted 8ow patterns at Y = 2:48 m plane are nearly thesame, and nearly the same velocity pro6les for the wall jet8ow are obtained (Fig. 10). But at the iteration step 14,604,the predicted jet 8ow pattern di)ers much from those atthe above two steps, and much di)erent velocity pro6les atX = 1 m, Z = 0 m and X = 1 m, Z = 0:25 m are obtained.To further investigate such a 8ow phenomenon, a

full-room con6guration with a mesh size of 60 × 55 × 68(the other half of the room is mirrored from Mesh1) is usedand both steady-state and time-dependent simulations arecarried out. In the steady-state simulations, it is found thatthe wall jet 8ow sometimes turns to one side of the room inthe course of iteration and then turns back to the symme-try plane. Fig. 12 is an example of the 8ow pattern underthe ceiling (Y = 2:48 m) at di)erent iteration steps froma steady-state simulation in full-room con6guration. Themesh is locally re6ned from X = 0 ∼ 0:3 m, Y = 2:13 ∼2:5 m and Z = −0:355 ∼ 0:355 m. It clearly shows thatthe 8ow is not symmetric. The 8ow pattern changes also ina quasi-periodic manner as the iteration progresses. It canbe seen for example that at the iteration steps 26,464 and48,340, the 8ow patterns are nearly the same, and the jet

8ow always turns to one side of the room—but at di)erentiteration steps the degree of asymmetry changes.A time-dependent simulation using the same con6gura-

tion and the same mesh resolution is also carried out. Tominimize the numerical truncation errors, the simulation isdone using the double precision solver in FLUENT. Simi-lar change of 8ow patterns as in the steady-state simulationis observed in the time-dependent simulation. Fig. 13 com-pares the time history of the mass 8ow rate at the outletand the Z velocity at the point of (1, 2.45, 0), i.e. at 1 mdistance from the di)user and 0:05 m below the ceiling onthe symmetry plane. It can be seen that the 8ow becomes“quasi-steady” after about 120 s, and then the 8ow “sweeps”from one side of the symmetry plane to the other side irreg-ularly at X = 1 m, the Z velocity at the point (1, 2.45, 0)changes its sign accordingly, and there is a clear correlationbetween the 8uctuations of the Z velocity and the mass 8owrate at the outlet: the phase of the Z velocity 8uctuation isopposite to the phase of the mass 8ow rate 8uctuation.In Fig. 14, the time histories of Z velocities at point (1,

2.45, 0) and points (2.2, 2.48, 0) are compared. It can beseen that at the point (2.2, 2.48, 0), the Z velocity does notchange its sign, but has a very small positive value (its meanvalue is about 0:027 m=s). The mean value of the Z velocityat the point (1, 2.45, 0) is also positive and is approximately0:0478 m=s. It means that the jet 8ow is always asymmetricand turns to one side of the symmetry plane, but the degree ofasymmetry changes with time—the same result is observedin the steady-state simulation as shown in Fig. 12. It can alsobe seen that the 8uctuation of Z velocity at these two pointshas an opposite phase too, but the phase of the 8uctuation


Fig. 12. An example of the predicted 8ow asymmetry near the room ceiling (Y = 2:48 m) in a full-room con6guration at di)erent iteration stages.(a) Velocity vector, (b) Velocity contour.

of Z velocity at the point (2.2, 2.48, 0) has a little lag. Thisis reasonable because the changes at the point (1, 2.45, 0)need some time to be transported to the point (2.2, 2.48, 0).Fig. 15 compares the time history of velocity magnitude attwo symmetric points (2:2; 1:2;−0:5) and (2.2, 1.2, 0.5) inthe occupied zone. It clearly shows that the degree of 8owasymmetry changes with time and that in the time interval520 ∼ 550 s, the velocity magnitude at the two points isnearly the same. It means that although the jet 8ow is alwaysasymmetric, the 8ow in the occupied zone can be symmetricsometimes. Fig. 16 shows the time history of the magnitudeof the velocity at the point (2.2, 2.48, 0.5). It can be seen

that after about 520 s, the magnitude of the velocity at thatpoint approaches to a 6xed value, the maximum 8uctuationis only about 0:002 m=s.It seems that at a ventilation rate of 3ACH, there is an

intrinsic instability in the 8ow, perhaps it is near a criticalvalue of Reynolds number which represents the ratio of con-vective and di)usive rates of momentum transfer. A verysmall time step (0:005 s) must be used in the time-dependentsimulation. When the time step is increased to 0:008 s, thecalculation at each time step converges in only two or threeiterations, but then suddenly in one time step even aftermore than 30 iterations the calculation does not converge,


Flow Time (s)

Z V

elo

city

(m

/s)

Mas

s F

low

Rat

e (k

g/s

)

0 100 200 300 400 500 600 700-0.1 -0.0366

-0.05 -0.03645

0 -0.0363

0.05 -0.03615

0.1 -0.036

0.15 -0.03585

Vz at (1, 2.45, 0)Mass Flow Rate at Outlet

Fig. 13. Time history of mass 8ow rate at the outlet and Z velocity at thepoints (1, 2.45, 0) (mesh size: 60× 55× 68, full-room con6guration).

Flow Time (s)

Z V

elo

city

(m

/s)

0 100 200 300 400 500 600 700-0.1

-0.05

0

0.05

0.1

0.15

Point (1, 2.45, 0)Point (2.2, 2.48, 0)

Fig. 14. Time history of Z velocities at the points of (1, 2.45, 0) and(2.2, 2.48, 0) (mesh size: 60× 55× 68, full-room con6guration).

and then the calculation diverges quickly. It seems that thereare some high frequency disturbances occurring in the 8owoccasionally which trigger the change of the 8ow pattern,but the 8ow is not completely unstable but changes in a“quasi-periodic” manner. Chen [27] has discussed unsteadyand unstable 8ow problems in ventilation 8ows in both nu-merical simulations and experiments. He also suggested thatmultiple solutions may exist for a special 8ow and the nu-merical simulation can pick one solution at one time andother solution at another time. In the present numerical studywith the steady-state simulations, it is observed that aftera certain number of iterations, the residuals for the 8ow

Flow Time (s)

Vel

oci

ty (

m/s

)

350 400 450 500 550 600 650 7000.04

0.0425

0.045

0.0475

0.05

0.0525

0.04580

0.04452

0.04826

0.04516

0.04814

0.045940.04368

Point (2.2, 1.2, 0.5)Point (2.2, 1.2, -0.5)

Fig. 15. Time history of the velocity magnitude at two symmetric pointsof (2.2, 1.2, 0.5) and (2.2, 1.2, −0:5) in the occupied zone (mesh size:60× 55× 68, full-room con6guration).

Flow Time (s)

Vel

oci

ty (

m/s

)

0 100 200 300 400 500 600 7000.4

0.42

0.44

0.46

0.48

0.5

Velocity at (2.2, 2.48, 0.5)

Fig. 16. Time history of the velocity magnitude at the point (2.2, 2.48,0.5) (mesh size: 60× 55× 68, full-room con6guration).

variables no longer decrease but stay at some stable valueswith more or less regular oscillations, and the oscillationsare not damped as also shown in Chen et al. [27]. But inthe time-dependent simulations, after a long enough tran-sient regime with damped oscillations, the 8ow tends to asteady-state regime (for t ¿ 700 s, Figs. 15 and 16).


Fig. 17. Comparison of calculated velocity and turbulent kinetic energy pro6les with di)erent turbulence models at the jet center line (Z =0 m, X =1 m,2:2 m).

3.7. Comparison of the predicted jet pro=les withdi8erent turbulence models

The jet pro6les predicted with di)erent turbulence mod-els and with local mesh re6nement (Mesh1+LR1) are com-pared with experimental data in Figs. 17 and 18. It can beseen that the RNG k–� model gives the best overall re-sults, the SST k–! model with transitional 8ow correction(low-Re version of the model) can yield a reasonable predic-tion for the jet velocity pro6les, but for the turbulent kineticenergy pro6les the prediction is less satisfactory. When us-ing the standard k–� model and the realizable k–� model,the calculation converges very slowly. The standard k–�model and the SST k—!model can predict the recirculation8ow at the upper left corner, while the realizable k–� modelcannot.The RSM model in FLUENT is mainly based on the

model proposed by Gibson et al. [20]. It contains a

wall-re8ection term in its pressure–strain model to accountfor the in8uence of the walls, which tends to damp thenormal stress perpendicular to the walls while enhancingthe stresses parallel to the walls [22]. It can be seen fromFigs. 17 and 18 that the inclusion of the wall-re8ection termunderpredicts the maximum velocity at the jet center planebut improves the prediction of the velocity pro6les andthe turbulent kinetic energy pro6les at the two side planesparallel to the center plane. Further investigation revealsthat without the wall-re8ection term, the RSM model canpredict the small recirculation 8ow at the upper left cornerof the room, but when the wall-re8ection term is included,the recirculation 8ow tends to diminish. Fig. 19 showsa comparison of the calculated 8ow 6elds at the upperleft corner using RSM model with/without wall-re8ectionterm.Since the momentum supplied by the di)user is mainly

contained at the jet center plane, the inclusion of the


Fig. 18. Comparison of calculated velocity and turbulent kinetic energy pro6les with di)erent turbulence models at two planes parallel to the symmetryplane (X = 1 m, Z = 0:25 m, 0:5 m) (the same notes as in Fig. 17).

Fig. 19. Comparison of the 8ow 6eld calculated with RSM model and with/without wall-re8ection term at the symmetry plane of the room (a) Withoutwall-re8ection term, (b) With wall-re8ection term.


wall-re8ection term in the RSM model will underpredictmore of the total momentum than when this term is notincluded.

4. Discussion

The above results showed that the RNG k–� model to-gether with local mesh re6nement yields a good predictionof the jet pro6les when momentum model is used for thenozzle di)user. However, the successful use of the momen-tummodel is not unconditional: it was found that there existsan optimum dimension of the momentum source cell in thestreamwise direction (X direction in Fig. 8) for the correctprediction of the jet pro6les. At 3ACH, the dimension ofthe momentum source cell in the X direction, TX0, shouldbe about 0.014–0:018 m. When using a value less than0:014 m, the maximum velocity in the jet pro6les will beunderpredicted; on the other hand, when using a value higherthan 0:018 m, the maximum jet velocity in the jet pro6leswill be overpredicted. For example, when TX0 =0:0108 m,the predicted maximum jet velocities are 0:977 m=s at X =1 m and 0:663 m=s at X = 2 m, while the measured maxi-mum jet velocities are 1:078 m=s at X = 1 m and 0:69 m=sat X = 2:2 m; thus they are underpredicted about 9.37 and3.91%, respectively; when TX0 = 0:021 m, the predictedmaximum jet velocity at X=1 m is nearly the same as that ofthe measurement, but at X =2:2 m, the predicted maximumjet velocity is 0:7463 m=s, i.e., overpredicted about 8.16%.Because experimental data exist for only one ventilation rate(3ACH), it is not clear whether this value is Reynolds num-ber dependent or whether we can 6nd a scaling law for de-termining the optimum dimension of the momentum sourcecell. In the present study, it is found that when the dimen-sion of the momentum source cell in the streamwise direc-tion is maintained between 0.014 and 0:018 m, little dif-ference can be found among the predictions from di)erentmeshes. Tests have been done with Mesh1 (60× 55× 34),Mesh2 (66× 61× 38), Mesh3 (80× 61× 38) as shown inFigs. 6 and 7 and with the same local mesh re6nement asshown in Fig. 8. The predicted jet pro6les from these meshesare nearly the same. Another important point is that themesh resolution in the proximity of the di)user must be highenough to minimize numerical di)usion, especially in theimpinging region, where very steep velocity gradients exist.Fig. 9 clearly shows the importance of proper grid resolu-tion in this region; when the grid is not 6ne enough, the re-circulation 8ow at the upper left corner of the room cannotbe reproduced.It can be seen from Figs. 6, 7, 17 and 18 that the jet ve-

locities at the lower part of the jet 8ow (Y 6 2:3 m) areunderpredicted especially at the side section of Z = 0:5 m,which is the region of jet entrainment. Thus, the main dis-advantage of the momentum model is that it cannot accountwell for jet entrainment, especially in the vicinity of the dif-

fuser. On the other hand, the tiny-box model used by Chenet al. [10] also underpredicts the jet velocities in this region,and they did not give the comparison of their prediction atthe two side sections (Z =0:25 and 0:5 m) with the experi-mental measurements of Ewert et al. [14]. Thus the perfor-mance of the box model in this region is unknown. Furtherinvestigation revealed that the discrepancy is mainly causedby the incorrect prediction of the spanwise and crosswisevelocity components, i.e., the 3D development of the jet.Fig. 20 is a comparison of the predicted velocity magnitudepro6les vs. X velocity pro6les with experimental measure-ments at X = 1 m before the di)user and it can be seenthat the agreement of the predicted X (streamwise) veloc-ity pro6les with those of the experimental measurements isexcellent.The 8ow asymmetry is repeatedly observed both in

steady-state simulation and in time-dependent simulationin the full-room con6guration. It may be caused by someintrinsic instability mechanism in the 8ow. When a sim-ulation is carried out in the half-room con6guration, theimposed symmetry boundary condition at the symmetryplane limits the development of the 8ow asymmetry but achange of 8ow pattern can still be observed (Fig. 11). Theresults shown in Fig. 10 indicate that even though the 8owpattern changes from time to time, the predicted jet velocitypro6les still correlate reasonably well with the experimentalmeasurements.

5. Concluding remarks

It can be concluded that the momentum model togetherwith the RNG k–� turbulence model and local mesh re6ne-ment can yield a good prediction for the wall jet 8ow is-sued from the HESCO nozzle di)user. It is also found thatthe RNG k–� model is very robust and the calculation con-verges smoothly for this special case. The momentum modelis very simple to use and the only empirical input neededis the e)ective 8ow area of the di)user which, in general,does not di)er very much from the gross 8ow area (in thepresent case 0:00855 m2 vs. 0:00918 m2, the di)erence be-ing 6.9%). In case that no experimental measurement of thee)ective 8ow area is available, using the gross 8ow areashould not lead to too large an error. Attention should bepaid in choosing the dimension of the momentum source cellin the streamwise direction. When no experimental data ex-ist for calibrating the optimum dimension of the momentumsource cell in the streamwise direction, an estimation can beattained by comparing the predicted velocity pro6les withdi)erent momentum source cell sizes, i.e., di)erent sizes inthe streamwise direction. The predicted jet pro6les can beused as the boundary condition for box model or prescribedvelocity model when a turbulence model other than the RNGk–� model is needed to account for other 8ow features in aventilated space.


Velocity Magnitude (m/s)

Ro

om

Hei

gh

t (m

)

0 0.2 0.4 0.6 0.8 1 1.22

2.1

2.2

2.3

2.4

2.5

X=1m, Z=0mMesh1+LR1Mesh1+LR2Ewert et al. (1991)

X Velocity (m/s)-0.25 0 0.25 0.5 0.75 1 1.25

2

2.1

2.2

2.3

2.4

2.5

X=1m, Z=0mMesh1+LR1Mesh1+LR2Ewert et al. (1991)


Ro

om

Hei

gh

t (m

)

0 0.2 0.4 0.6 0.8 1 1.2

2.1

2.2

2.3

2.4

2.5

X=1m, Z=0.25mMesh1+LR1Mesh1+LR2Ewert et al. (1991)

X Velocity (m/s)-0.25 0 0.25 0.5 0.75 1 1.25

2

2.1

2.2

2.3

2.4

2.5



Ro

om

Hei

gh

t (m

)

0 0.2 0.4 0.6 0.8 1 1.22

2

2.1

2.2

2.3

2.4

2.5


X Velocity (m/s)-0.25 0 0.25 0.5 0.75 1 1.25

2

2.1

2.2

2.3

2.4

2.5


Fig. 20. Comparison of the predicted velocity magnitude and X velocity pro6les with experimental measurement for the HESCO nozzle di)user (meshsize: 60× 55× 34 with local mesh re6nement).

Acknowledgements

Special thanks to Dr. Schwarz of Fluent Inc., who kindlysent us the experimental data of Ewert et al. [14] and Heikki-nen [13] for the HESCO nozzle di)user, and also for theinspiring discussions. The calculations were mainly carriedout on the AMD Athlon PC cluster at L3M, part of thecalculations were carried out on the massive parallel ma-chine SGI Origin 3800 at the Centre Informatique Nationalde l’Enseignement SupVerieur (CINES). Technical supportfrom D. FougWere and S. Fayolle of L3M and P. Falandryof CINES is gratefully acknowledged. This study was sup-

ported by a study grant from the French Embassy in Chinawhich is also gratefully acknowledged.

References

[1] Nielsen PV. Flow in air conditioned rooms, Ph.D. Thesis, TechnicalUniversity of Denmark, 1974.

[2] Chen Q. Comparison of di)erent k–� models for indoor air 8owcomputations. Numerical Heat Transfer Part B 1995;28:353–69.

[3] Chen Q. Prediction of room air motion by Reynolds-stress models.Building and Environment 1996;31(3):233–44.

[4] Fontaine JR, Biolley F, Rapp R, SVerieys JC, Cunin JC. Analysisof a three dimensional ventilation 8ow: experimental validation on


a waters scale model of numerical simulations. Numerical HeatTransfer Part A 1994;26:431–51.

[5] Murakami S, Kato S. Numerical and experimental study on roomair8ow—3-D predictions using the k–� turbulence model. Buildingand Environment 1989;24(1):85–97.

[6] Nielsen PV, Restivo A, Whitelaw JH. The velocity characteristicsof ventilated rooms. Journal of Fluids Engineering 1978;100:291–8.

[7] Nielsen PV, Restivo A, Whitelaw JH. Buoyancy-a)ected 8ows inventilated rooms. Numerical Heat Transfer 1979;2:115–27.

[8] Nielsen PV. Description of supply openings in numerical models forroom air distribution. ASHRAE Transactions 1992;98(1):963–71.

[9] Nielsen PV. The box method—a practical procedure for introductionof an air supply device in CFD calculation. Institute forBygningsteknik, Aalborg University, 1997.

[10] Chen Q, Srebric J. Simpli6ed di)user boundary conditions fornumerical room air8ow models. ASHRAE RP-1009, 2000.

[11] Lemaire AD. Annex-20 air 8ow patterns within buildings: roomair and contaminant 8ow, evaluation of computational methods—Subtask-1 Summary Report. TNO Building and ConstructionResearch, 1993.

[12] Peng SH. Modeling of turbulent 8ow and heat transfer for buildingventilation. Ph.D. Thesis, Chalmers University of Technology, 1998.

[13] Heikkinen J. Modeling of supply air terminal for room air 8owsimulation. Proceedings of 12th AIVC Conference, Ottawa, Canada,September 24–27, 1991.

[14] Ewert M, Renz U, Vogl N, Zeller M. De6nition of the8ow parameters at the room inlet devices—measurements andcalculations. Proceedings of 12th AIVC Conference, Ottawa, Canada,September 24–27, 1991.

[15] Skovgaard M, Nielsen PV. Modeling complex geometries in CFD—applied to air 8ow in ventilated rooms, Proceedings of 12th AIVCConference, Ottawa, Canada, September 24–27, 1991.

[16] Emvin P, Davidson L. A numerical comparison of threeinlet approximations of the di)user in case E1 Annex 20.Fifth International Conference on Air Distributions in Rooms,ROOMVENT’96, Yokohama, Japan, vol. 1, 1996, pp. 219–26.

[17] Buchanan CR. CFD Characterization of a mechanically ventilatedoBce room: the e)ects of room design on ventilation performance.Ph.D. Thesis, University of California, 1997.

[18] Djunaedy E, Cheong KWD. Development of a simpli6ed techniqueof modeling four-way ceiling air supply di)user. Building andEnvironment 2001;37(4):393–403.

[19] Loomans MGLC. The measurement and simulation of indoor air8ow. Ph.D. Thesis, Eindhoven University of Technology, 1998.

[20] Gibson MM, Launder BE. Ground e)ects on pressure 8uctuationsin the atmospheric boundary layer. Journal of Fluid Mechanics1978;86:491–511.

[21] Launder BE, Reece GJ, Rodi W. Progress in the development ofa Reynolds-stress turbulence closure. Journal of Fluid Mechanics1975;68(3):537–66.

[22] Fluent Inc. Fluent 6 user manual. 6-58-72, 10-1-102. 2001.[23] Gan G. Prediction of turbulent buoyant 8ow using an RNG k–�

model. Numerical Heat Transfer Part A 1998;33:169–89.[24] Versteeg HK, Malalasekera W. Introduction to computational 8uid

dynamics. New York: Longman Group Ltd.; 1995.[25] Awbi HB. Application of computational 8uid dynamics in room

ventilation. Building and Environment 1989;24(1):73–84.[26] Zhang G, Morsing S, Bierg B, Svidt K, StrHm JS. Test room

for validation of air8ow patterns estimated by computational 8uiddynamics. Journal of Agricultural Engineering Research 2000;76:141–8.

[27] Chen Q, Jiang Z. Signi6cant questions in predicting room air motion.ASHRAE Transactions: Symposia Part I 1992;98:929–39.

Modeling of the HESCO nozzle diffuser used in IEA Annex-20 experiment test room

Documents

Transcript of Modeling of the HESCO nozzle diffuser used in IEA Annex-20 experiment test room