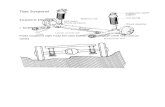
Model matematika suspensi motor
-
Upload
raful-al-khawarizmi -
Category
Engineering
-
view
338 -
download
18
Transcript of Model matematika suspensi motor

2. Model Matematika Suatu Masalah
2.1 Penurunan Rumus Matematika dari Suatu Masalah
Seperti yang dijelaskan dalam pengantar dalan bab ini bahwa perumusan matematis suatu
permasalahan yang berbentuk sebuah model matematis adalah hal yang sangat penting sebelum
menyelesaikan masalah itu sendiri.
Sebagai contoh akan diberikan fenomena yang akan di buat model matematikanya
sebagai berikut:
Sebuah massa m kg diberikan pada pegas yang semula memiliki panjang L0 meter, pada
t=0. Massa berpindah dari jarak X0 meter dengan kecepatan V0 meter/menit. Diasumsikan
gerakan terjadi secara vertical dengan aturan bahwa jarak diukur positif dengan arah menurun
kebawah. Secara matematis harus ditentukan gaya yang menyebabkan terjadinya pergerakan.
Pertama anggap bahwa pegas dalam posisi setimbang dimana massa menggantung secara bebas
dari pegas tanpa ada gerakan. Gaya yang menyebabkan massa dalam posisi setimbang adalah :
1. gaya oleh grafitasi : Fg = m.g
2. Gaya pegas Fs , yang menyebabkan perpindahan pegas dari panjang awalnya, lihat
gambar 2.1.
Gaya yang terakhir ini (Fs ) diambil dari hukum HOOKE :
Ketika pegas direnggangkan atau dimampatkan dengan jarak L dari panjang awalnya sama
dengan gaya pegas : Fs = - k L

Dimana k adalah konstanta positip yang disebut konstanta pegas dengan satuan meter/kg. Jika L0
menunjukkan regangan pegas dari posisi kesetimbangan statisnya, maka : Fs = - k L0
Karena sistemnya dalam kesetimbangan statis, maka gaya pegas harus diseimbangkan oleh gaya
grafitasi : Fs + Fg = 0
Fg = - Fs
m.g = k L0 ....(2.1.1)
Anggap situasi ketika massa telah menimbulkan gerakan X(t) yang menunjukkkan posisi massa
pada waktu t dan missal X=0 bertepatan dengan sistem pada posisi setimbang, maka persamaan
gaya yang menyebabkan massa bergerak sebagai berikut:
1.
Gaya grafitasi : Fg = m.g (2.1.2)
2. Gaya pegas Fs pada waktu t perpindahan total pegas dari panjang awalnya adalah L0 +
X(t), menurut hukum Hooke :
Fs = - k ( L0 + X(t)) (2.1.3)
3. Gaya yang disebabkan oleh tekanan pada luasan tertentu (Fd). Secara umum gerakan
disebabkan karena gas, misalnya tekanan udara, seperti yang ditunjukkan pada gambar
2.2 , merupakan sistem gas luar, misalkan dashphot . Diasumsikan bahwa gaya yang
disebabkan oleh tekanan gas secara langsung sebanding dengan kecepatan massa Fd = - c
...(2.1.4)
Dimana c adalah konstanta positip yang disebut konstanta gas. Tanda negatip
dikarenakan Fd selalu menyebabkan arah berlwanan dengan gerakan.

Gambar 2.1 Model sederhana dari sistem pegas dengan redaman
4.
2. Gaya pendorong luar F(t) yang ditimbulkan. Sebagai contoh bagian puncak pegas dari
massa itu sendiri, boleh disebut gaya luar.
Jumlah gaya yang menyebabkan sistem beraksi akan dijumlahkan dengan menggunakan hukum
Newton II, diperoleh persamaan diferensial yang menyebabkan gerakan adalah :
atau:
(2.1.5)
dengan kondisi nilai awal yang harus diberikan adalah : X(0) = x0 , = v0
Oleh karena itu untuk menentukan gerakan dari sistem harus mengatasi MNA :
(2.1.6)

Selanjutnya akan kita bahas lebih dahulu untuk kasus F(t) = 0 dan untuk kasus F(t) 0 kita
bahas pada bagian berukutnya.
2.2. OSILASI BEBAS DARI SEBUAH SISTEM MEKANIS
Pada bagian ini, kita akan mempelajari gerak dari sistem pegas bermassa dengan asumsi
bahwa tidak ada gaya luar yang mempengaruhi sistem tersebut. Dengan demikian, kita
asumsikan bahwa sistem diatur sedemikian rupa sehingga interaksi luar tidak diperhitungkan.
Dalam rumus umum dari pembahasan sebelumnya, ditetapkan fungsi F(t)=0, jadi nilai awal
untuk masalah (2.1.5) diturunkan menjadi
(2.2.1)
Selanjutnya kita akan lebih banyak membahas tentang persamaan diferensial itu sendiri, selama
kondisi awal tidak mempengaruhi sifat dari rumus di atas. Pandang PD :
(2.2.2)
yaitu persamaan diferensial linear dengan koefisien konstan homogen , dapat diselesaikan
dengan menggunakan teknik penyelesaian dari pembahasan sebelumnya. Kami membagi
pembahasan dari rumus (2.2.2) ke dalam beberapa kasus/kejadian.
Kejadian 1 : TANPA REDAMAN (DAMPING).
Pertama kita membahas kasus dimana tidak terdapat redaman (c = 0). Ini merupakan kasus
paling sederhana yang dapat muncul dan akan sangat penting untuk memahami kasus yang lebih
umum seperti ini. Persamaan diferensial (2.2.2) kita menjadi :
(2.2.3)
Dimana
(2.2.4)
Persamaan diferensial dengan koefisien konstan (2.2.3) memiliki penyelesaian umum :
(2.2.5)

Dalam kasus ini diperkenalkan dua konstanta baru A0 dan yang didefinisikan dalam c1 dan
c2.
(2.2.6)
dengan
(2.2.7)
Tugas: Dengan subtitusi (2.2.7) tunjukkan bahwa
.....(2.28)
Jelasnya, gerakan yang dinyatakan oleh (2.2.8) adalah gerak periodik. Kita mengacu kepada
gerakan seperti gerak harmonik sederhana. Gambar (2.2.2) menggambarkan gerakan ini untuk
tipe nilai konstanta dan .
gambar 2.2.2
Gerak Harmonik sederhana Massa berosilasi kontinu dengan amplitude konstan
Adapun penamaan untuk ketiga konstanta diatas adalah :
: ampiltudo gerakan
: frekuensi sudut system
: fase gerakan
Periode osilasi (waktu yang diperlukan untuk melakukan satu putaran), T, adalah
(2.2.9)

sehingga frekuensi osilasi, f adalah
Kejadian 2 : DENGAN GAYA REDAMAN.
Sekarang kita membahas gerak dari sistem pegas jika gaya redam konstan. Untuk kasus
ini, Persamaan karakteristik untuk (2.2.2) adalah :
Dengan akar-akar : Karakter sstem tergantung pada akar-akar
karakteristiknya : real berbeda, real kembar dan komplek. Ketiga situasi ini akan muncul pada
besarnya c2 -4km . Umtuk pegas bermassa tertentu hanya dampingnya yang dapat diubah, hal ini
akan memunculkan terminology berikut :
Kita katakana sistem dalam kondisi :
a) Underdamped (redaman yg kecil/terkontrol ) c2 < 4km akar komplek
b) Critically damped ( redaman yang kritis) c2 = 4km akar real kembar
c) overdamped ( redaman yang berlebihan) c2 > 4km akar real berbeda
Penyelesaian DP (2.2.2) untuk kondisi :
a)X(t) = (2.2.10)
b)X(t) = (2.2.11)
c)X(t) = (2.2.12)
dalam ketiga kasus ini kita memiliki definisi : yang menyatakan bahwa tidak ada
gerakan untuk t bernilai tak hingga. Atau berasimtotis ke 0 untuk t .
Kejadian 2a : Underdamped.
Dalam kasus ini posisi massa pada waktu t dinyatakan dalam (2.2.10), gerak harmonik
sederhana juga berlaku dalam hal ini, yaitu ketika c=0. Misalkan dua konstanta yang
didefinisikan oleh :

Penyelesaian (2.2.10) dapat ditulis:
(2.2.13)
Dapat dilihat bahwa massa berosilasi sekitar . Fungsi gerak ini digambarkan pada
gambar (2.2.3) untuk kasus ketika X(0)>0 dan (dx/dt)(0)>0
Pada umumnya, gerak ini adalah bersifat osilasi, tetapi tidak periodik. Amplitudo gerakan
mencapai npl bersaman dengan waktu yang cukup lama, dan T waktu antara dua posisi
maksimum ( atau minimum) dari X(t) memiliki nilai konstan :
Kejadian 2b : Criticaldamped.
Kasus ini muncul ketika c2 = 4 km, masukkan pada persamaan (2.2.10) diperoleh PD yang
menerangkan gerak tersebut adalah :
Dengan penyelesaian umum :
X(t)=
(2.2.14)
Sekarang redaman sangat keras/kritis, sehingga sistem dapat mencapai titik kesetimbangan
sekali. Jadi tidak ditemukan sifat osilasi. Jika ditetapkan posisi awal :

sehingga dengan mudah terlihat bahwa (10.2.14) dapat ditulis dalam bentuk :
Akibatnya, sistem akan melewati posisi setimbang yang diberikan oleh X0 dan
yang memiliki tanda berlawanan. Sketsa dari gerak tersebut digambarkan pada (2.2.4)
Kejadian 2c : Overdamped.
Dalam kasus ini kita memiliki c2 -4km atau Akar-akar dari persamaan karakteristik :
Misalkan , penyelesaian umu PD (2.2.2) adalah
Selama c, k, m bernilai positip, maka akar-akar dari persamaan karakteristik adalah negatip, yang
menyatakan bahwa kedua faktor di X(t) saling meniadakan menurut fungsi waktu. Tidak ada
osilasi. Gerakan mirip dengan gerak pada kasus critical damped. Sistem dapat mencapai posisi
setimbang hanya sekali. Hal ini diilustrasikan dalam gambar (2.2.5).

2.3 OSILASI OLEH GAYA LUAR .
Sekarang kita pertimbangkan situasi ketika sistem massa pegas ditarik keatas dengan gaya luar.
Sebagai contoh, Puncak dari gaya pegas yang saling tarik menarik tiba-tiba bergetar, misalnya
seseorang yang berjalan melintas diatasnya. Sebagaimana yang ditunjuk pada bagian
sebelumnya, PD yang tepat untuk mendiskripsikan perubahan sIstem adalah :
Situasi penting akan muncul ketika gaya yang diaplikasikan secara periodik dalam waktu
tertentu, dan pembahasan kita batasi pada gaya gerak dalam bentuk:
dimana F0 dan adalah konstan. Oleh karena itu PD dasar menjadi :
(2.3.1)
Akan kita bagi menjadi beberapa bagian pembahasan :
Bagian 1 : Tanpa redaman.
Anggap c = 0 pada ( 2.3.1), menjadi :
(2.3.2)
dimana dinotasikan sebagai frekwensi sudut dari sistem dan bernilai
Fungsi komplemen untuk (2.3.2) adalah :
yang dapat ditulis dalam bentuk :
(2.3.3)

dimana adalah konstan. Penyelesaian partikulir bergantung pada keadaan atau
.
Untuk , penyelesaian partikulir dengan operator D diperoleh :
(2.3.4)
sehingga penyelesaian umum (2.3.2) :
(2.3.5)
Hasil pergerakan ini terdiri dari super posisi dua model geteran harmonic sederhana. Salah satu
darinya mempunyai frekwensi sudut dari system. Dan model lainnya memiliki frekwensi gaya
gerak. Maka pergerakannya berupa gelombang dan dibatasi untuk semua waktu, tetapi tidak
periodic pada umumnya. Tentu saja, ini bisa ditunjukkan (lihat gambar (2.3.1)) bahwa gerakan
secara periodik hanya terjadi bila perbandingan merupakan bilangan real. Dapat
dikatakan bahwa
(2.3.6)
dimana p dan q merupakan bilangan bulat positip. Dalam kasus ini , periode untuk gerakan ini
adalah
dimana p dan q merupakan bilangan bulat terkecil yang diberikan olen (2.3.6). Type gerakan
(nonperiodik) dari pers(2.3.5) diberikan oleh gambar (2.3.1).

Untuk Resonansi, Ketika frekwensi gaya gerak bertepatan (sama) dengan frekwensi
system , penyelesaian partikulir dengan operator D dari PD :
(2.3.7)
adalah :
(2.3.8)
Maka penyelesaian umum dari (2.3.7) adalah
(2.3.9)
Kita ketahui bahwa gerakan merupakan sebuah gelombang tetapi amplitudonya meningkat tanpa
batas t . Fenomena ini terjadi ketika frekwensi gerak dan frekwensi system sama besarnya
disebut dengan Resonansi. Dan ini tidak bisa diberikan gaya/tekanan berlebih . Sebagai contoh ,
kejadian resonansi pada waktu tertentu kadang disebabkan elastisitas pegas mendekati batas
ambang, dan karena itu system akan rusak. Situasi seperti ini digambarkan pada gambar (2.3.2)

dibawah ini.
Bagian 2 : Dengan Redaman.
Perhatikan persamaan berikut :
(2.3.9)
comana . Penyelesaian partikulir dengan komputasi secara langsung diperoleh :
(2.3.10)
dan dapat ditulis sebagai :
(2.3.11)
dimana , dan
dan . Dan penyelesaian umum dari (2.3.9) adalah :

(2.3.12)
Untuk nilai t yang sangat besar maka xc dominant, untuk alas an ini fungsi komplemen
merupakan bagian Transien dari penyelesaian , dan xp dikatakan bagian Steady state
Dari penyelesaian. Kita tinjau (2.3.12) kembali sebagai superposisi dua getaran harmonic satu
dengan resonansi dan lainnya tanp resonansi. Getaran harmonik sederhana ini kadang
berfrekwensi sama dengan frekwensi gaya gerak benda.
Bagian untuk resonansi kritis maupun over resonansi adalah sama, karena kedua bagian fungsi
complement menghasilkan penyelesaian eksponensial dan penyelesaian steady state. Macam
macam gerakan dari system gaya mekanik dengan resonansi ditunjukkan gambar (2.3.3)