Kuliah Teknik Digital
-
Upload
ririn-yulia -
Category
Documents
-
view
299 -
download
5
description
Transcript of Kuliah Teknik Digital

Buku Pegangan Kuliah
TEKNIK DIGITAL
Oleh:
Bowo Eko Cahyono
Jurusan Fisika – FMIPA Universitas Jember
2015

ii
Kata Pengantar
Buku ini disusun sebagai panduan dan outline mata kuliah Teknik Digital
yang merupakan mata kuliah wajib di Jurusan Fisika FMIPA Universitas Jember.
Beberapa referensi di “cited” agar mahasiswa dapat memperkaya materi dalam
diktat ini dari beberapa sumber sehingga dapat meningkatkan pemahaman yang
didapatnya.
Beberapa contoh persoalan diberikan dalam setiap bahasan materi untuk
mempermudah mahasiswa dalam memahami secara riil dan dapat menerapkan
konsep-konsep yang diberikan. Format huruf dalam beberapa contoh soal sengaja
diberikan dalam font yang berbeda untuk menunjukkan kelurusan posisi bilangan
yang dioperasikan sehingga dapat lebih menekankan pemahaman terhadap
penjelasan yang telah diberikan. Latihan soal-soal di setiap akhir bab dimaksudkan
agar mahasiswa dapat mengukur kompetensinya setelah mempelajari materi yang
diberikan dalam bab tertentu.
Kontribusi dari berbagai pihak yang membantu buku ini tersusun, sanagt
diapresiasi. Tentunya input dan feedback yang konstruktif terus terbuka bagi
penulis agar ke depannya dapat menyempurnakan beberapa kekurangan yang
mungkin masih ditemukan dalam buku ini.
Jember, 24 August 2015
Penulis

iii
KONTRAK PERKULIAHAN
Mata Kuliah : Teknik Digital SKS : 2 – 1 SKS Koord. Kelas : Ridlo / 085733052347 Materi
1. Pendahuluan 2. Sistem Bilangan
a. Sistem Bilangan Desimal b. Sistem Bilangan Biner c. Sistem Bilangan Oktal d. Sistem Bilangan Hexadesimal e. Aritmatika biner
3. Gerbang Logika 4. Rangkaian Logika
a. Gerbang Kombinasi b. Aljabar Boole c. Map Karnaugh d. Konversi Gerbang e. Half Adder dan Full Adder
5. Flip-flop 6. Register 7. Pencacah dan Pewaktu 8. Dekoder dan Multiplekser 9. ADC dan DAC
Referensi 1. Ibrahim, K F. 1991. Digital Techniques. 1st ed. Longman, London United
Kingdom. 2. Mano, M Morris, and Maichael D Ciletti. 2013. Digital Design. 5th ed.
Pearson, New Jersey. 3. Maini, Anil K. 2007. Digital Electronics: Principles, Devices and
Applications. John Wiley & Sons Ltd, Chichester – England. 4. Tokheim, Roger L. 1990. Digital Electronics. 2nd ed. McGraw Hill, New
York. 5. Brewster, Hilary D. 2009. Digital lelectronics. Oxford Book Company,
Jaipur

iv
Penilaian UTS 35% UAS 35% Tugas & Quiz 25% Presensi 5%

v
DAFTAR ISI
Kata Pengantar ........................................................................................................ ii
KONTRAK PERKULIAHAN ............................................................................... iii
DAFTAR ISI ............................................................................................................. v
DAFTAR GAMBAR .............................................................................................. vii
BAB 1 PENDAHULUAN ................................................................................... 1
BAB 2 SISTEM BILANGAN .............................................................................. 3
2.1 Sistem Bilangan Desimal .................................................................................. 3
2.2 Sistem Bilangan Biner ...................................................................................... 4
2.3 Sistem Bilangan Oktal ...................................................................................... 9
2.4 Sistem Bilangan Hexadesimal ........................................................................ 10
2.5 Aritmatika biner .............................................................................................. 12
2.5.1. Penjumlahan ....................................................................................... 13
2.5.2. Pengurangan ....................................................................................... 14
2.5.3. Bilangan biner bertanda ..................................................................... 15
2.5.4. Komplemen satu dan komplemen dua ............................................... 15
2.5.5. Perkalian ............................................................................................ 17
2.5.6. Pembagian .......................................................................................... 17
Soal-soal latihan: ...................................................................................................... 18
BAB 3 GERBANG LOGIKA ........................................................................... 20
3.1 Gerbang AND ................................................................................................. 20
3.2 Gerbang OR .................................................................................................... 23
3.3 Gerbang NOT ................................................................................................. 24
3.4 Gerbang NAND .............................................................................................. 25
3.5 Gerbang NOR ................................................................................................. 25
3.6 Gerbang XOR ................................................................................................. 26
Soal-soal latihan (Tokheim, 1994): .......................................................................... 27
BAB 4 RANGKAIAN LOGIKA ...................................................................... 28
4.1 Gerbang kombinasi ......................................................................................... 28
4.2 Aljabar Boole .................................................................................................. 29

vi
4.3 Map Karnaugh ................................................................................................ 30
4.4 Konversi gerbang ............................................................................................ 33
4.5 Half adder dan Full adder ............................................................................... 34
Soal-soal latihan: ...................................................................................................... 36
BAB 5 FLIP - FLOP ......................................................................................... 40
5.1 Latch (memori satu bit) .................................................................................. 41
5.2 Flip-flop S-R ................................................................................................... 42
5.3 Flip-flop D ...................................................................................................... 45
5.4 Flip-flop J-K ................................................................................................... 46
5.5 Flip-flop T ....................................................................................................... 47

vii
DAFTAR GAMBAR
Gambar 1. 1 Contoh gambar sebuah multimeter analog ............................................................ 1
Gambar 1. 2 Contoh gambar sebuah pico ampere meter digital ................................................. 2
Gambar 3. 1 Simbol dan tabel kebenaran gerbang logika AND dua masukan ........................ 21
Gambar 3. 2 Analogi gerbang logika AND dua masukan dengan rangkaian listrik ................ 21
Gambar 3. 3 Konfigurasi pin pada IC 7411 (gerbang AND 3 masukan). ................................ 22
Gambar 3. 4 Simbol dan tabel kebenaran gerbang logika AND tiga masukan ........................ 22
Gambar 3. 5 Simbol dan tabel kebenaran gerbang logika OR dua masukan ............................ 23
Gambar 3. 6 Analogi gerbang logika OR dua masukan dengan rangkaian listrik .................... 23
Gambar 3. 7 Simbol dan tabel kebenaran gerbang logika OR tiga masukan ........................... 24
Gambar 3. 8 Simbol dan tabel kebenaran gerbang logika NOT ............................................... 24
Gambar 3. 9 Simbol dan tabel kebenaran gerbang logika NAND ........................................... 25
Gambar 3. 10 Simbol dan tabel kebenaran gerbang logika NOR ............................................. 26
Gambar 3. 11 Simbol dan tabel kebenaran gerbang logika XOR ............................................. 26
Gambar 4. 1. Kombinasi gerbang AND dan NOT ekuivalen dengan NAND ........................... 28
Gambar 4. 2. (a) Rangkaian gerbang logika 2 masukan dan (b) jumlah cell yang mungkin
pada map Karnaugh untuk penyederanaan rangkaian. ........................................................ 30
Gambar 4. 3. Map Karnaugh untuk rangkaian gerbang logika pada Gambar 4. 2. ................... 31
Gambar 4. 4. Rangkaian gerbang logika dengan tiga masukan. ............................................... 32
Gambar 4. 5. Map Karnaugh untuk rangkaian gerbang logika pada Gambar 4. 4. ................... 32
Gambar 4. 6. Gerbang NAND dan NOR yang berfungsi sebagai gerbang NOT. ..................... 33
Gambar 4. 7. Fungsi gerbang OR yang didapat dari rangkaian 3 gerbang NAND. .................. 34
Gambar 4. 8. Efisiensi penggunaan IC dengan konversi gerbang dari rangkaian logika
yang diberikan pada Gambar 4. 2. ...................................................................................... 34
Gambar 4. 9. Rangkaian half adder dan tabel kebenarannya. ................................................... 35
Gambar 4. 10. Rangkaian half adder yang disusun dari gerbang-grbang dasar. ....................... 35
Gambar 4. 11. Rangkaian half adder yang disusun hanya dari gerbang NAND. ...................... 35
Gambar 4. 12. Rangkaian full adder dan tabel kebenarannya. .................................................. 36

viii

ix
DAFTAR TABEL Tabel 2. 1 Contoh delapan bilangan biner pertama dengan 20 sebagai LSB dan 22
sebagai MSB. 5
Tabel 2. 2 Contoh kolom bilangan biner untuk konversi desimal ke biner. Untuk
bilangan desimal yang lebih tinggi, dapat ditambahkan kolom di sebelah kiri MSB
sesuai dengan kebutuhan. ...................................................................................................... 5
Tabel 2. 3 Kesamaan bilangan desimal dalam tiga tipe bilangan BCD ...................................... 9
Tabel 2. 4 Variasi enam belas bilangan berbeda dalam sistem bilangan
hexadesimal yang bersesuaian dengan nilai dalam bilangan desimal dan bilangan
biner. 11
Tabel 2. 5 Contoh penghitungan dalam penjumlahan biner dengan kolom. ................. 14
Tabel 2. 6 Contoh penghitungan dalam penngurangan biner dengan kolom. ............... 14

1
BAB 1 PENDAHULUAN
Dalam kehidupan sehari-hari kita sering berhadapan dengan bilangan untuk
menyatakan nilai-nilai dari suatu besaran yang merepresentasikan sebuah kuantitas
fisik seperti temperatur, tegangan listrik, panjang suatu benda, dan lain sebagainya.
Ada dua cara yang dapat digunakan untuk mengungkapkan nilai-nilai numerik dari
kuantitas fisik tersebut. Cara pertama adalah analog dan cara kedua adalah digital.
Analog adalah cara merepresentasikan nilai-nilai suatu besaran dalam suatu
bilangan yang kontinu dalam interval dua nilai ekstrim (Maini, 2007). Sebagai
contoh, dalam pengukuran analog sebuah temperatur ruangan kita dapat
menuliskan 27oC atau 27.35oC atau 27.351208oC bergantung pada ketelitian alat
ukur yang kita gunakan. Contoh lain jika kita ingin melaporkan hasil perngukuran
tegangan listrik dalam sebuah rangkaian, kita dapat menuliskannya seperti 46 V
atau 45.73 V atau 45.72915426V. Dalam sebuah pengukuran yang menggunakan
alat ukur analog, ketelitian hasil pengukuran selain ditentukan oleh alat yang
digunakan juga dapat dipengaruhi oleh cara pembacaan yang dilakukan oleh
pengamat. Contoh alat ukur analog ditunjukan dalam Gambar 1. 1.
Gambar 1. 1 Contoh gambar sebuah multimeter analog

2
BAB 1 PENDAHULUAN
Berikutnya, nilai digital merepresentasikan nilai dari suatu besaran dalam
step-step nilai atau nilai-nilai diskret. Sebagai contoh, temperatur sebuah oven
diberikan dalam nilai dengan step 1oC misalnya 70 oC, 71 oC, 72 oC dan seterusnya.
Step-step nilai yang ditampilkan bisa kita atur sesuai dengan kebutuhan dan juga
bergantung kepada ketelitian alat yang digunakan. Sebuah alat ukur digital yang
teliti bahkan dapat mengukur arus listrik sampai orde pico ampere (Keithley,
2015). Ini berarti step nilai yang digunakan dalam alat ukur tersebut adalah 10-12.
Gambar 1. 2 Contoh gambar sebuah pico ampere meter digital
Dalam teknologi masa kini yang menggunakan sistem komputerisasi, sistem
dan teknologi digital mempunyai peran yang sangat penting. Oleh karena itu alat
ukur digital lebih disukai dan banyak dipakai karena lebih mudah dalam konversi
dan transfer data. Keuntungan dari sistem digital adalah relatif mudah dalam
mendesain, mempunyai ketelitian yang lebih tinggi, dapat diprogram, tahan
terhadap noise, lebih mudah dalam menyimpan data, dapat didesain dalam bentuk
IC (integrated circuit) sehingga dapat dibuat untuk fungsi yang kompleks dengan
ukuran yang lebih kecil.
Besaran-besaran yang ada di alam ini seperti temperatur, kecepatan, tekanan
dan kelembaban udara, serta beberapa yang lain bagaimanapun adalah besaran-
besaran yang analog. Untuk itu diperlukan pengetahuan dan ketrampilan untuk
dapat mengubah besaran-besaran analog tersebut ke dalam bentuk digital agar
dapat beradaptasi dengan teknologi digital saat ini. Dasar-dasar tentang teknik
digital, konversi analog ke digital dan sebaliknya adalah hal penting yang perlu kita
pelajari dan akan dibahas dalam bab-bab selanjutnya dalam buku ini.

3
BAB 2 SISTEM BILANGAN
Ada beberapa sistem bilangan yang kita kenal yaitu bilangan biner, bilangan
oktal, bilangan desimal, dan bilangan hexadesimal. Dari beberapa sistem bilangan
tersebut, yang biasa kita pakai adalah bilangan desimal. Dalam bab ini kita kembali
akan membahas 4 sistem bilangan yang telah kita sebutkan di atas dan juga
membahas bagaimana konversi dari sistem bilangan satu ke sistem bilangan yang
lain.
2.1 Sistem Bilangan Desimal
Bilangan desimal adalah bilangan yang paling sering kita gunakan dalam
kehidupan sehari-hari dalam berbagai bidang seperti perdagangan, perhitungan
matematika dan statistika, perbankan dan lain sebagainya. Sistem bilangan ini
adalah bilangan berbasis 10 yang artinya dikenal 10 macam bilangan yang berbeda
yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Untuk menyatakan bilangan selanjutnya yaitu
bilangan setelah 9 adalah kembali lagi mulai dari 0 dengan tambahan digit bilangan
kedua pada orde yang lebih tinggi yaitu 1. Dengan kata lain kita menuliskan sebuah
bilangan yang lebih tinggi satu step dari 9 adalah bilangan 10. Selanjutnya digit
kedua bertambah satu step menjadi 2, 3, 4,...,9 dan setelah itu digit pertama
berubah menjadi 2 diikuti dengan 0 atau ditulis sebagai 20 dan seterusnya.
Dalam sistem bilangan desimal, kita sering menyebut bilangan pada digit
pertama sebagai “satuan”, digit kedua sebagai “puluhan”, digit ketiga sebagai
“ratusan” dan seterusnya. Dalam sistem bilangan berpangkat basis 10 kita
menuliskannya sebagai 100, 101, 102,...... Untuk bilangan desimal pecahan kita
menuliskannya sebagai bilangan berpangkat negatif atau 10-1 untuk , 10-2 untuk
, 10-3 untuk , dan selanjutnya.
Nilai atau beasr sebuah bilangan desimal adalah merupakan jumlahan
masing-masing digit dikalikan dengan nilai posisinya. Sebagai contoh bilangan

4
BAB 2 SISTEM BILANGAN
125,375 terdiri atas bilangan bulat 125 dan bilangan pecahan 0.375. Kita dapat
menuliskan bilangan tersebut sebagai:
a. Bilanan bulat 125 = 1 x 102 + 2 x 101 + 5 x 100
= 100 + 20 + 5 = 125
b. Bilangan pecahan 0.375 = 3 x 10-1 + 7 x 10-2 + 5 x 10-3
= 0.3 + 0.07 + 0.005 = 0.375
Konsep nilai dari posisi dalam bilangan berpangkat seperti contoh di atas
juga dapat diterapkan secara umum untuk beberapa sistem bilangan yang akan kita
bahas pada sub-bab berikutnya.
2.2 Sistem Bilangan Biner
Bilangan biner adalah bilangan berbasis 2 yang memiliki arti hanya ada dua
bilangan yang dikenal dalam sistem bilangan ini yaitu bilangan “0” dan “1”.
Seperti halnya pada bilangan desimal, bilangan ketiga kembali dimulai dari 0
dengan tambahan digit 1 di depannya. Dalam bilangan biner dikenal istilah”bit”
untuk menyatakan satu digit bilangan biner (Ibrahim, 1991). Bit paling kanan
dalam sebuah bilangan biner disebut dengan Least Significant Bit (LSB) dan bit
paling kiri disebut dengan Most Significant Bit (MSB).
Seperti halnya bilangan desimal, bilangan biner juga dapat dinyatakan dalam
bilangan berpangkat basis 2 yaitu 20, 21, 22, dan seterusnya untuk bilangan bulat
dan 2-1, 2-2, 2-3, dan seterusnya untuk bilangan pecahan. Contoh delapan bilangan
bulat biner diberikan dalam Tabel 2. 1. Bilangan selanjutnya dapat dihitung dengan
menggunakan prinsip yang sama dengan bilangan desimal. Sebagai contoh kita
berikan bilangan biner 110011 merepresentasikan bilangan desimal berikut.
110011 = 1x25 + 1x24 + 0x23 + 0x22 + 1x21 + 1x20
= 32 + 16 + 0 + 0 + 2 + 1 = 51
Jadi bilangan biner 110011 sama dengan 51 dalam bilangan desimal. Untuk
membedakan penulisan bilangan dalam sistem yang berbeda, kita menggunakan
subscript sebagai bilangan basisnya. Bilangan desimal kita gunakan subscript 10
dan bilangan biner menggunakan subscript 2. Dari contoh bilangan biner yang
sudah kita hitung di atas, kita dapat menuliskannya 1100112 = 5110.

5
BAB 2 SISTEM BILANGAN
Tabel 2. 1 Contoh delapan bilangan biner pertama dengan 20 sebagai LSB dan 22 sebagai MSB.
Desimal Biner
22 21 20
0 0 0 0
1 0 0 1
2 0 1 0
3 0 1 1
4 1 0 0
5 1 0 1
6 1 1 0
7 1 1 1
Konversi desimal ke biner
Konversi bilangan desimal ke biner dapat dilakukan dengan dua cara
(Ibrahim, 1991). Cara pertama adalah dengan menggunakan tabel kolom biner
seperti ditunjukkan pada Tabel 2. 2. Pada baris pertama kita melakukan konversi
bilangan desimal 22 ke bilangan biner. Karena 22 kurang dari 32 maka kolom 32
bernilai 0. Selanjutnya kolom 16 diisi 1 karena nilai 22 lebih dari 16. Masih ada
sisa ilai 6 jika 22 dikurangi 16 sehingga kolom 4 dan kolom 2 masing-masing diisi
1 dan kolom terakhir nilainya nol karena sudah tak ada lagi sisa bilangan dari 22.
Serupa dengan cara di atas, konversi bilangan desimal untuk baris-bari selanjutnya
dapat dilakukan dan hasil selengkapnya ada pada Tabel 2. 2.
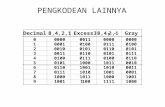
Tabel 2. 2 Contoh kolom bilangan biner untuk konversi desimal ke biner. Untuk bilangan desimal yang lebih tinggi, dapat ditambahkan kolom di sebelah kiri MSB sesuai dengan kebutuhan.
Desimal Kolom biner Output
biner 32 16 8 4 2 1
22 0 1 0 1 1 0 10110
40 1 0 1 0 0 0 101000
17 0 1 0 0 0 1 10001
34 1 0 0 0 1 0 100010

6
BAB 2 SISTEM BILANGAN
Cara kedua adalah dengan metode pembagian seperti yang akan diuraikan
berikut ini. Bilangan desimal yang akan dikonversi dibagi dengan 2 sebagai basis
bilangan biner, dan hal ini dilakukan terus menerus sampai hasil baginya sama
dengan 0. Sisa bilangan hasil pembagian secara urut merupakan bilangan biner
hasil konversi dengan sisa hasil pembagian yang pertama merupakan LSB dan sisa
pembagian yang terakhir merupakan MSB.Sebagai contoh marilah kita konversi
bilangan desimal 47 menjadi bilangan biner.
47/2 = 23 sisa 1 (LSB)
23/2 = 11 sisa 1
11/2 = 5 sisa 1
5/2 = 2 sisa 1
2/2 = 1 sisa 0
1/2 = 0 sisa 1 (MSB)
Dari hasil perhitungan pembagian di atas kita dapat menuliskan bilangan biner
hasil konversinya dari MSB ke LSB atau dengan kata lain hasil konversi desimal
47 ke biner adalah 101111.
Bilangan biner pecahan
Seperti telah disinggung sebelumnya bahwa bilagan hiner dapat dinyatakan
dalam sistem bilangan berpangkat basis 2 baik pangkat negatif maupun positif.
Bilangan basis 2 berpangkat negatif untuk menyatakan bilangan biner pecahan.
Seperti halnya yang berlaku dalam sistem bilangan desimal, penulisan bilangan
bulat dan pecahan dipisahkan dengan dengan tanda koma. Hal ini juga sama
berlaku pada sistem bilangan biner. Konvensi yang digunakan adalah semakin ke
kiri penulisan bilangannya maka semakin besar nilai pangkatnya. Perlu diingat
disini bahwa untuk pangkat bilangan negatif, nilai -1 lebih besar dari -2, dan -2
lebih besar dari -3, demikian seterusnya.
Sebagai contoh akan kita berikan beberapa bilangan biner pecahan seperti
berikut: 0,12 = 2-1 = 1/2 = 0,510
0,001 = 2-3 = 1/8 = 0,12510
Dengan demikian jika kita memiliki bilangan biner 1101,101 maka:

7
BAB 2 SISTEM BILANGAN
1101,1012 = 1x23 + 1x22 + 0x21 + 1x20 + 1x2-1 + 0x2-2 + 1x2-3
= 8 + 4 + 0 + 1 + 1/2 + 0 + 1/8
= 8 + 4 + 0 + 1 + 0,5 + 0 + 0,125 = 13,62510
Jika kita ingin melakukan konversi bilangan desimal pecahan ke dalam
bentuk bilangan biner pecahan, maka yang kita lakukan adalah mengalikan
bilangan desimal pecahan tersebut dengan 2 kemudian menuliskan bilangan bulat
hasil perkalian tersebut sebagai digit untuk bilangan biner dan sisa pecahannya
dikalikan lagi dengan 2. Hal ini dilakukan sampai mendapatkan hasil kali sama
dengan 1 dan sisanya 0. Sebagai contoh bilangan 0,812510 dapat dikonversi jadi:
0,8125 x 2 = 1,625 bulat 1 (MSB) sisa 0,625
0,625 x 2 = 1,25 bulat 1 sisa 0,25
0,25 x 2 = 0,5 bulat 0 sisa 0,5
0,5 x 2 =1 bulat 1 (LSB) sisa 0
Sehingga 0,812510 = 0,11012.
Sistem bilangan BCD
Sistem bilangan BCD (the binary coded decimal) adalah tipe bilangan biner
yang digunakan untuk menyatakan suatu bilangan desimal dalam bentuk biner
(Maini, 2007). Dalam sistem BCD, setiap digit bilangan desimal direpresentasikan
dengan 4 digit bilangan biner. Hal ini tentu saja akan sangat memudahkan dalam
melakukan konversi baik dari BCD ke desimal maupun sebaliknya dari desimal ke
BCD. Sebagai contoh kita akan dapat langsung melakukan konversi bilangan
desimal 23,15 menjadi bilangan BCD 0010 0011, 0001 0101. Hal ini tidak bisa
dengan cepat kita lakukan saat kita melakukan konversi dari desimal ke biner
seperti yang dibahas dalam sub-bab sebelumnya.
Contoh konversi BCD yang diberikan di atas tipe kode BCD 8421. Artinya
bobot setiap digit bilangan biner adalah 8, 4, 2, dan 1 berurutan dari MSB ke LSB
dalam satu grup 4 digitan biner. Ada dua tipe kode BCD yang lain yakni BCD 4221
dan BCD 5421. Selengkapnya kesamaan bilangan BCD masing-masing tipe dengan
desimal diberikan dalam

8
BAB 2 SISTEM BILANGAN
Tabel 2. 3.

9
BAB 2 SISTEM BILANGAN
Tabel 2. 3 Kesamaan bilangan desimal dalam tiga tipe bilangan BCD
Desimal BCD 8421 BCD 4221 BCD 5421
0 0000 0000 0000
1 0001 0001 0001
2 0010 0010 0010
3 0011 0011 0011
4 0100 1000 0100
5 0101 1001 1000
6 0110 1100 1001
7 0111 1101 1010
8 1000 1110 1011
9 1001 1111 1100
Dari 3 sistem BCD seperti ditunjukkan di atas, sistem BCD dengan
pembobotan 8421 adalah sistem yang paling populer dan banyak digunakan karena
memiliki konsistensi dengan posisi perpangkatan dalam bilangan biner yang
dibahas sebelumnya. Oleh karena itu untuk selanjutnya, setiap kali kita memakai
sistem bilangan BCD maka kita mengacu pada sistem BCD 8421 kecuali apabila
disebutkan secara khusus.
2.3 Sistem Bilangan Oktal
Bilangan oktal adalah bilangan berbasis 8 yang berarti hanya ada 8 nilai yang
ada yaitu 0, 1, 2, 3, ... , 7. Seperti dua sistem bilangan sebelumnya angka ke
sembilan yaitu angka 8 ditulis kembali mulai dari 0 dengan tambahan angka 1 di
depannya atau 810 = 108. Posisi nilai bilangan bulat oktal dapat juga dinyatakan
dalam 80, 81, 82, 83, dan seterusnya sedangkan bilangan oktal pecahan dinyatakan
dengan 8-1, 8-2, 8-3, dan seterusnya. Bilangan oktal 3725 bila dintakan dalam
desimal menjadi:
37258 = 3x83 + 7x82 + 2x81 + 5x80
= 1536 + 448 + 16 + 5
= 200510

10
BAB 2 SISTEM BILANGAN
Sebaliknya bila kita ingin mengubah bilangan desimal menjadi bilangan
oktal, cara mudah yang bisa kita gunakan adalah cara pembagian seperti yang
diraikan dalam konversi desimal ke biner dengan penyesuaian basis bilangannya.
Misalnya, ita akan mengkonversi bilangan desimal 5142 ke bilangan oktal maka:
5142/8 = 642 sisa 6 (LSB)
642/8 = 80 sisa 2
80/8 = 10 sisa 0
10/8 = 1 sisa 2
1/8 = 0 sisa 1 (MSB)
Dengan demikian hasil konversi bilangan desimal 5142 ke dalam bilangan oktal
adalah 12026 ata dengan kata lain 514210 = 120268.
Bilangan oktal dan bilangan biner
Basis bilangan oktal dan biner memiliki hubungan perpangkatan atau 8 = 23.
Dari hubungan ini kita dapat menyatakan satu digit bilangan oktal menjadi 3 digit
bilangan biner. Hal ini juga akan mempermudah konversi bilangan oktal ke biner
dan sebaliknya. Konversi bilangan oktal ke biner dilakukan dengan mengubah
setiap digit bilangan oktal menjadi 3 digit bilangan biner. Sebagai contoh bilangan
oktal 537 maka angka 58 = 1012, angka 38 = 0112, dan angka 78 = 1112 sehingga
kita dapat menyatakan 5378 = 101 011 1112.
Sebaliknya konversi biner ke oktal dapat dilakukan dengan mengelompokkan
setiap tiga digit bilangan biner dimulai dari belakang untuk diubah menjadi satu
digit bilangan oktal. Misalnya bilangan biner 11110011001 bisa kita kelompokkan
menjadi 11 110 011 001 dan kalau setiap kelompok kita ubah ke dalam bilangan
oktal akan menjadi 3631. Kesimpulannya bilangan 111100110012 = 36318. Hal ini
adalah konversi yang sangat mudah untuk dilakukan.
2.4 Sistem Bilangan Hexadesimal
Bilangan hexadesimal atau dikenal dengan bilangan hexa adalah bilangan
basis 16 yang memiliki 16 variasi bilangan yang berbeda. Selengkapnya variasi
bilangan tersebut diberikan dalam

11
BAB 2 SISTEM BILANGAN
Tabel 2. 4. Seperti halnya sistem bilangan lain yang telah dibahas
sebelumnya, posisi nilai dari setiap digit bilangan hexa dinyatakan sebagai 160, 161,
162, 163, dan seterusnya. Bilangan 14B16 dapat dinyatakan dengan 1x162 + 4x161 +
Bx160 = 33110. Subscript 16 merepresentasikan basis dari bilangan hexadesimal.
Tabel 2. 4 Variasi enam belas bilangan berbeda dalam sistem bilangan hexadesimal yang bersesuaian dengan nilai dalam bilangan desimal dan bilangan biner.
Desimal Hexadesimal Biner
0 0 0000
1 1 0001
2 2 0010
3 3 0011
4 4 0100
5 5 0101
6 6 0110
7 7 0111
8 8 1000
9 9 1001
10 A 1010
11 B 1011
12 C 1100
13 D 1101
14 E 1110
15 F 1111
Jika kita ingin melakukan konversi bilangan desimal menjadi bilangan
hexadesimal, metode pembagian dengan bilangan 16 dapat diterapkana seperti
contoh yang diberikan dalam dua sub-bab sebelumnya. Bilangan desimal 69510
dapat dikonversi menjadi bilangan hexadesimal sebagai berikut.
695/16 = 43 sisa 7 (LSB)
43/16 = 2 sisa 11
2/16 = 0 sisa 2 (MSB)

12
BAB 2 SISTEM BILANGAN
Jadi dari perhitungan di atas dapat kita simpulkan bahwa 69510 = 2B716
Bilangan hexadesimal dan bilangan biner
Basis bilangan hexadesimal merupakan hasil perpangkatan dari basis
bilangan biner. Bilangan 16 adalah sama dengan 24. Berdasarkan hal ini maka satu
digit bilangan hexadesimal dapat dinyatakan dengan 4 digit bilangan biner. Seperti
yang sudah kita lakukan pada bilangan oktal, bilangan hexadesimal 4C19 dapat
dikonversi menjadi bilangan biner seperti berikut. Bilangan 416 = 01002, bilangan
C16 = 11002, bilangan 116 = 0001, dan bilangan 916 = 10012. Dengan kata lain
4C1916 = 100 1100 0001 10012.
Sebaliknya bila kita akan mengkonversi bilangan biner menjadi bilangan
hexadesimal maka kita mengelompokkan bilangan biner tersebut empat-empat
dimulai dari belakang yang merupakan digit LSB. Ambil contoh bilangan biner
1011110010001101112 dapat dikelompokkan menjadi 10 1111 0010 0011 0111
sehingga: 102 = 216 (MSB)
11112 = F16
00102 = 216
00112 = 316
01112 = 716 (LSB)
Jadi 1011110010001101112 = 2F23716.
2.5 Aritmatika biner
Aritmatika biner adalah operasi hitung yang diterapkan pada sistem bilangan
biner. Seperti halnya operasi hitung pada bilangan desimal, dalam aritmatika biner
juga dikenal penjumlahan, pengurangan, perkalian, dan pembagian. Dalam
penjumlahan dan pengurangan, operasi dilakukan dengan memperhatikan posisi
koma pada bilangan yang dioperasikan sedangkan pada perkalian dan pembagian
perhatian pada posisi koma itu tidak perlu diperhatikan. Selengkapnya masing-
masing operasi dalam aritmatika biner diuraikan dalam kelompok-kelompok
bahasan di bawah ini.

13
BAB 2 SISTEM BILANGAN
2.5.1. Penjumlahan Serupa dengan penjumlahan pada desimal, penjumlahan biner dilakukan
dengan menyusun bilangan-bilangan yang dijumlahkan dari atas ke bawah dengan
memperhatikan posisi komanya. Maksudnya signifikasi atau bobot bilangan yang
sama ditempatkan pada kolom yang sama. Aturan-aturan dasar pada penjumlahan
biner adalah:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 simpan 1
Apabila dalam penjumlahan ada nilai simpanan, maka ilai tersebut dijumlahkan
dengan bilangan di depannya atau bilangan dengan bobot posisi yang lebih tinggi.
Sebagai contoh kita ingin menjumlahkan 10112 + 1102 maka penghitungannya:
1011 110 10001
Dari contoh perhitungan di atas dapat dijelaskan bahwa penjumlahan
dilakukan dari bit LSB yaitu 1+0=1. Selanjutnya pindah ke digit depannya yaitu
1+1=0 simpan 1. Nilai simpanan ini kita jumlahkan dengan digit depannya
sehingga 0+1+1(sumpanan)=0 simpan 1. Kembali lagi nilai simpanan ini kita
jumlahkan dengan digit depan lanjutannya yang hanya tinggal satu angka menjadi
1+1 (simpanan)=0 simpan 1. Simpanan ini adalah nilai terakhir yang kita letakkan
di paling depan sebagai MSB karena tidak ada angka lagi yang perlu dijumlahkan.
Dengan demikian 10112 + 1102 = 100012.
Untuk lebih memperjelas pemahaman, berikut ini diberikan contoh lain
penjumlahan biner yang ditampilkan dan format kolom. Misalnya tentukan hasil
penjumlahan dari 101102 + 111102 + 111012. Perhatikan nilai-nilai dalam kolom
pada Tabel 2. 5 khususnya nilai simpanan dan nilai hasil penjumlahannya.

14
BAB 2 SISTEM BILANGAN
Tabel 2. 5 Contoh penghitungan dalam penjumlahan biner dengan kolom.
26 25 24 23 22 21 20
1 0 1 1 0
1 1 1 1 0
1 1 1 0 1
Simpan 1 2 2 2 1 0
Jumlah 1 0 1 0 0 0 1
Dengan demikian 101102 + 111102 + 111012 = 10100012.
2.5.2. Pengurangan Dalam pengurangan bilangan biner, posisi kedua bilangan yang akan
dioperasikan juga harus diperhatikan. Seperti halnya penjumlahan, setiap digit
harus diposisikan pada bobot yang sama dalam satu kolom. Bahasan ini hanya akan
menjelaskan pengurangan biner dimana bilangan yang dikurangi adalah lebih besar
dari bilangan pengurangnya sehingga hasil dari pengurangan tersebut adalah
bilangan positif. Untuk lebih mempermudah dan memperjelas proses operasi,
contoh pengurangan berikut yaitu 11002 - 10102 diberikan dalam bentuk operasi
kolom seperti terlihat pada Tabel 2. 6.
Tabel 2. 6 Contoh penghitungan dalam penngurangan biner dengan kolom.
24
(16)
23
(8)
22
(4)
21
(2)
20
(1)
Pinjam (22)
1 1 0 0
1 0 1 0
Hasil 0 0 1 0

15
BAB 2 SISTEM BILANGAN
2.5.3. Bilangan biner bertanda Dalam matematika kita jarang menuliskan tanda “+” untuk bilangan-bilangan
positif. Tetapi kita pasti memberi tanda “-“ untuk menyatakan bilangan-bilangan
yang bernilai kurang dari nol atau bilangan negatif. Dalam sistem digital yang
basisnya adalah bilangan biner, sayangnya tidak ada tempat untuk menuliskan
tanda + atau - seperti kalau kita bekerja dengan bilangan desimal. Dalam sistem
biner kita hanya mengenal 0 atau 1.
Bilangan biner bertanda adalah sebuah cara untuk mengenali bilangan biner
positif atau negatif. Bit yang paling kiri dalam sebuah bilangan biner bertanda
mengindikasikan tanda bilangan. Angka 1 menyatakan tanda bahwa bilangan biner
tersebut adalah negatif, sedangkan angka 0 menandakan bahwa bilangan biner
tersebut adalah positif. Untuk mempermudah mengenali bilangan biner bertanda,
bit tanda yang terletak paling kiri diletakkan dalam kurung siku. Sebagai contoh
bilangan -5 dituliskan sebagai [1]101 sedangkan bilangan +9 dituliskan [0]1001.
Bilangan biner bertanda 8 bit mempunyai nilai maksimal sebesar 7 bit biner
atau 27-1 atau 127 karena bit paling kiri digunakan untuk menyatakan tanda
bilangan. Misalnya bilangan 1101 0101 = [1]101 0101 = - (26+0+24+0+22+0+20)
atau sama dengan -85. Sedangkan bilangan 0110 0111 = [0]110 0111 atau sama
dengan + (26+25+0+0+22+21+20) = +103. Jadi bilangan biner bertanda sebanyak 8
bit mempunyai kemungkinan untuk menyatakan nilai minimum – (27-1) atau -127
dan nilai maksimum +(27-1) atau +127. Secara umum, untuk bilangan biner n bit,
nilai minimum dan maksimum yang mampu dinyatakan adalah ± (2n-1 – 1).
2.5.4. Komplemen satu dan komplemen dua Dalam operasi aritmatika biner yang dalam hal ini adalah pengurangan,
penggunaan bilangan biner bertanda seperti diuraikan di atas tidaklah “applicable”.
Sebagai gantinya kita menggunakan bilangan komplemen dua. Dalam operasi
pengurangan kita mempunyai aturan bahwa A-B = A+(-B) atau sebaliknya B-A =
B+(-A).
Komplemen dua dari bilangan biner positif tetap sama dengan bilangan
awalnya. Untuk menyatakan bilangan negatif, komplemen dua didapatkan dengan
cara mencari bilangan komplemen satu dan menmbahkannya dengan angka 1.
Sedangkan bilangan komplemen satu diperoleh dengan menginversikan semua bit

16
BAB 2 SISTEM BILANGAN
bilangan termasuk bit tanda. Dengan kata lain komplemen satu diperoleh dengan
mengubah semua angka 0 menjadi 1 dan sebaliknya mengubah semua angka 1
menjadi 0. Untuk lebih memperjelas pengertian ini marilah kita ambil contoh
bilangan 110112 atau 2710. Komplemen satu dari 27 adalah 001002 dan komplemen
duanya adalah 001002 + 12 = 001012.
Sekarang marilah kita menerapkan konsep komplemen dua ini dalam operasi
pengurangan biner. Dalam hal ini kita juga memperhatikan bti tanda pada bilangan
yang dioperasikan. Kita ambil contoh 2110 – 1210 yang hasilnya adalah 910. Dalam
penulisannya, jumlah bit kedua bilangan yang dioperasikan harus sama banyaknya.
1210 = [0]011002 2110 = [0]101012
Komp 1 [1]100112 Komp 1 [1]010102
Komp 2 [1]101002 = -1210 Komp 2 [1]010112 = -2110
Maka 2110 -1210 = [0]101012 + [1]101002
= 1[0]010012
= [0]010012
Bilangan hasil operasi hanyalah sejumlah 5 bit angka sesuai dengan banyaknya bit
bilangan yang diperasikan. Sehingga bit keenam dari kanan adalah bit tanda dan
angka 1 disebelah kiri bit tanda diabaikan. Jadi 2110 -1210 = [0]010012 = 910.
Sebagai contoh kedua kita ambil 510 – 1710 yang hasilnya adalah -1210.
Seperti yang diuraikan di atas, penulisan banyaknya bit bilangan yang dioperasikan
adalah sama.
510 = [0]001012 1710 = [0]100012
Komp 1 [1]110102 Komp 1 [1]011102
Komp 2 [1]110112 = -510 Komp 2 [1]011112 = -1710
Maka 510 -1710 = [0]001012 + [1]011112
= [1]101002
Pada contoh soal kedua ini bit tanda pada bilangan hasil operasi adalah 1 yang
berarti hasilnya adalah bilangan negatif. Untuk hasil yang negatif, besarnya nilai
bilangan hasil harus dikonversi dulu ke komplemen duanya dengan catatan bit
tanda tidak ikut diproses. Komplemen dua dari 101002 adalah 010112 + 12 =
011002. Jadi hasil akhir dari 510 -1710 adalah bilangan negatif dengan besar nilai
011002 atau ditulis [1] 011002 = -1210.

17
BAB 2 SISTEM BILANGAN
2.5.5. Perkalian Dalam perkalian bilangan biner berlaku aturan seperti berikut:
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1, di sini tidak ada simpanan dan dan pinjaman
Pada prinsipnya perkalian bilangan biner ini sama seperti perkalian bilangan biner
yang sudah biasa kita lakukan. Untuk memperjelas aturan perkalian ini dalam
aplikasinya, marilah kita perhatikan dua contoh operasi perkalian bilangan biner
berikut.
1. 1010012 x 1102 atau dalam bilangan desimal 4110 x 610
101001 = 4110
110 = 610
000000 101001 101001 11110110 = 24610
2. 101112 x 112 atau dalam bilangan desimal 2310 x 310
10111 = 2310
11 = 310
11111 (nilai simpanan) 10111 10111 1000101 = 6910
2.5.6. Pembagian Pembagian dalam sistem bilangan biner dapat dilakukan dengan mengambil
analogi pada pembagian bilangan desimal. Proses pembagian dilakukan mulai dari
bilangan paling kiri (MSB) dan seterusnya sampai pada bilangan terakhir. Jika
bilangan yang dibagi bukan merupakan kelipana bilangan pembagi maka akan
didapatkan sisa dari hasil pembagian tersebut. Untuk memperjelas hal ini mari kita
lihat dua contoh pembagian bilangan biner dimana contoh pertama adalah
pembagian tanpa sisa dan contoh kedua adalah pembagian biner dengan sisa.
x
+
x
+

18
BAB 2 SISTEM BILANGAN
1. 1010102 : 1102 atau dalam bilangan desimal 4210 : 610
Hasil 111 = 710
Pembagi 110 101010 = 4210
110 = 610
01001 110 110 110 0 (tanpa sisa)
2. 1100112 : 10012 atau dalam bilangan desimal 5110 : 910
Hasil 101 = 510
Pembagi 1001 110011 = 5110
1001 = 910
111 000 1111 1001 110 (sisa 610)
Soal-soal latihan:
1. Lakukan operasi pengurangan bilangan-bilangan biner berikut ini dengan
mengambil nilai komplemen dua dari bilangan pengurang (bilangan kedua)
kemudian menjuumlahkannya dengan bilangan pertama.
a. 010012 011002
b. 000112 001112
2. Selesaikan operasi dari bilangan desimal -11 + (-2) dengan mengubahnya
terlebih dahulu menjadi bilangan biner dan gunakan metode komplemen dua.
3. Kalikan bilangan-bilangan biner berikut:
a. 10102 x 00112
b. 10112 x 01112
c. 10012 x 10102
4. Jumlahkan bilangan-bilangan BCD berikut:
a. 0110 + 0101
b. 0111 + 1000
c. 1001 + 1000
d. 0100 + 0110
-
-
-
-
-
-

19
BAB 2 SISTEM BILANGAN
5. Jumlahkan bilangan-bilangan hexadesimal berikut:
a. 3C16 + 2516
b. 1416 + 2816
c. 3B16 + DC16
d. 011016 + 1001016
6. Apakah perbedaan utama antara half acdder dan full adder ?
7. Selesaikan operasi pengurangan 18 – 4 dengan mengubah setiap bilangan
desimal ke dalam bentuk komplemen dua bilangan binernya.
8. Nyatakan penjumlahan desimal 26 + 27 dalam bentuk biner.
9. Nyatakan setiap bilangan biner bertanda berikut dalam bilangan desimal:
a. [0]0000101
b. [1]1111100
c. [1]1111000
Source: http://www.indiabix.com/digital-electronics/digital-arithmetic-operations-and-circuits/216002

20
BAB 3 GERBANG LOGIKA
Gerbang logika adalah sebuah blok dasar untuk membentuk rangkaian logika
digital (Paton, 1998). Gerbang logika bekerja dengan menggunakan sistem
bilangan biner seperti telah dibahas dalam bab sebelumnya. Dalam pembahasan
gerbang logika di sini, kita juga hanya mengenal dua jenis sinyal yaitu 1 atau 0.
Dalam sebuah rangkaian elektronik, sinyal 1 (logika tinggi) analog dengan
tegangan tinggi (5 volt) sedangkan sinyal 0 (logika rendah) analog dengan
tegangan rendah atau ground atau 0 volt.
Secara umum, hampir semua rangkaian logika atau sistem digital tersusun
dari tiga macam gerbang logika yaitu gerbang AND, OR, dan NOT (Singh et. al.,
2006). Pengetahuan dasar tentang gerbang-gerbang tersebut akan dibahas lebih
detail dalam sub-sub bab berikut dengan beberapa tambahan gerbang-gerbang
logika lain yang umum digunakan.
Hubungan antara masukan dan keluaran suatu gerbang logika juga akan
diperkenalkan dalam bentuk matematis untuk menyederhanakan penulisan dan
penyampaian. Hubungan masukan dan keluaran suatu gerbang logika secara
matematis diperkenalkan oleh seorang matematikawan dari Lincoln Inggris yang
bernama “George Boole”. Beliau membuat suatu persamaan matematis yang
dikenal dengan istilah ungkapan Boole. Ungkapan ini sangat penting dalam
penjelasan tentang gerbang logika khususnya dalam rangkaian logika,
penyederhanaan dan konversinya. Dalam bab ini hanya akan dibahas prinsip dasar
beberapa gerbang logika dan cara pengungkapannya.
3.1 Gerbang AND
Gerbang AND digunakan untuk menghasilkan keluaran bernilai 1 apabila
semua masukan yang diberikan padanya bernilai 1. Karena itu gerbang AND ada
juga yang menyebut sebagai gerbang “ all or nothing” atau gerbang semua atau
tidak (Tokheim, 1990). Maksudnya keluaran akan bernilai 1 (logika tinggi) jika
semua masukan 1. Jika tidak semua masukan bernilai 1 maka keluaran akan

21
BAB 3 GERBANG LOGIKA
menjadi 0 (logika rendah). Simbol dan tabel kebenaran gerbang AND diberikan
pada Gambar 3. 1.
Masukan Keluaran
A B Y
0 0 0
1 0 0
0 1 0
1 1 1
Gambar 3. 1 Simbol dan tabel kebenaran gerbang logika AND dua masukan
Karakteristik keluaran gerbang AND dapat juga dianalogikan dengan sistem
kerja rangkaian listrik seperti terlihat pada Gambar 3. 2. Masukan A dan B dalam
tabel kebenaran gerbang AND dimisalkan dengan saklar A dan B. Jika saklar
ditutup berarti masukan bernilai 1 dan sebalikknya jika saklar terbuka artinya
masukan gerbang bernilai 0. Jika kita perhatikan rangkaian pada Gambar 3. 2,
maka lampu hanya akan menyala jika kedua saklar ada dalam posisi tertutup.
Selain kondisi ini maka lampu tidak akan menyala atau dapat dikatakan bahwa
keluaran gerbang AND akan bernilai 0.
Gambar 3. 2 Analogi gerbang logika AND dua masukan dengan rangkaian listrik
Ungkapan boole untuk gerbang AND dua masukan dinyatakan seperti pada
persamaan 3.1 di bawah ini.
. = 3. 1
Dalam prakteknya terkadang dibutuhkan juga gerbang AND dengan tiga
masukan seperti yang ada pada IC 7411. Konfigurasi pin pada IC 7411 ditunjukkan
pada Gambar 3. 3.

22
BAB 3 GERBANG LOGIKA
Gambar 3. 3 Konfigurasi pin pada IC 7411 (gerbang AND 3 masukan).
Untuk simbol dan tabel kebenaran gerbang AND tiga masukan diberikan
pada Gambar 3. 4. Dalam gerbang 3 masukan ada 8 kemungkinan kombinasi
susunan masukan. Seperti halnya gerbang AND dua masukan, dalam gerbang
AND tiga masukan juga hanya menghasilkan keluaran 1 jika seluruh masukan
bernilai 1.
Masukan Keluaran
A B C Y
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
Gambar 3. 4 Simbol dan tabel kebenaran gerbang logika AND tiga masukan
Ungkapan boole untuk gerbang AND tiga masukan dinyatakan seperti pada
persamaan 3.2 di bawah ini.
. . = 3. 2

23
BAB 3 GERBANG LOGIKA
3.2 Gerbang OR
Gerbang OR akan memberika keluaran bernilai 1 jika ada salah satu
masukannya yang mempunyai nilai 1. Ada juga yang menyebut bahwa gerbang
OR adalah gerbang satu atau semua (Tokheim, 1990). Simbol dan tabel kebenaran
gerbang OR dengan dua masukan diberikan pada Gambar 3. 5.
Masukan Keluaran
A B Y
0 0 0
1 0 1
0 1 1
1 1 1
Gambar 3. 5 Simbol dan tabel kebenaran gerbang logika OR dua masukan
Seperti halnya gerbang AND, prinsip kerja gerbang OR juga dapat dijelaskan
dengan menggunakan analogi rangkaian listrik sederhana seperti terlihat pada
Gambar 3. 6. Lampu dalam rangkaian akan menyala jika minimal ada satu saklar
yang ditutup. Hal ini mengindikasikan bahwa keluaran gerbang OR akan bernilai 1
jika minimal ada satu masukan yang bernilai 1. Di sisi lain lampu tidak akan
menyala hanya jika kedua saklar dalam kondisi terbuka. Hal ini mempunyai
analogi bahwa keluaran gerbang OR hanya akan bernilai 0 jika kedua masukannya
0 dan selebihnya keluaran gerbang OR akan bernilai 1.
Gambar 3. 6 Analogi gerbang logika OR dua masukan dengan rangkaian listrik
Ungkapan boole untuk gerbang OR dua masukan dinyatakan seperti pada
persamaan 3.3 di bawah ini.
+ = 3. 3

24
BAB 3 GERBANG LOGIKA
Selanjutnya untuk gerbang OR yang terdiri dari 3 masukan, ada 8 kombinasi
masukan dimana hanya ada satu kombinasi yang memberikan keluaran 0 yaitu
pada saat ketiga masukannya semua bernilai 0, sedangkan tujuh kombinasi sisanya
akan menghasilkan keluaran bernilai 1. Selengkapnya tabel kebenaran gerbang OR
tiga masukan diberikan pada Gambar 3. 7.
Masukan Keluaran
A B C Y
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
Gambar 3. 7 Simbol dan tabel kebenaran gerbang logika OR tiga masukan
Ungkapan boole untuk gerbang OR tiga masukan dinyatakan seperti pada
persamaan 3.4 di bawah ini.
+ + = 3. 4
3.3 Gerbang NOT
Gerbang not dikenal juga dengan istilah inverter karena berfungsi untuk
mengubah masukan 0 menjadi 1 dan sebaliknya masukan yang bernilai 1 akan
dirubah menjadi 0. Gerbang NOT hanya mempunyai satu masukan dan hanya ada
dua kemungkinan kombinasi masukan seperti yang terlihat dalam tabel kebenaran
pada Gambar 3. 8.
Masukan Keluaran
A Y
0 1
1 0
Gambar 3. 8 Simbol dan tabel kebenaran gerbang logika NOT

25
BAB 3 GERBANG LOGIKA
Ungkapan boole untuk gerbang NOT dinyatakan seperti pada persamaan 3.5
di bawah ini.
= 3. 5
3.4 Gerbang NAND
Gerbang NAND dikenal juga dengan gerbang Not AND yang berarti bahwa
keluaran gerbang NAND merupakan inverse dari keluaran gerbang AND. Dengan
demikian gerbang NAND dapat juga dibentuk dengan menambahkan gerbang
NOT pada keluaran gerbang AND. Pada simbol gerbang NAND kita dapat melihat
tanda lingkaran pada kaki keluarannya yang melambangkan NOT. Susunan tabel
kebenaran gerbang NAND diberikan dalam tabel pada Gambar 3. 9. Kalau kita
bandingkan nilai keluaran dari gerbang NAND ini maka cocok jika susunan ini
merupakan inversi dari keluaran gerbang AND.
Masukan Keluaran
A B Y
0 0 1
1 0 1
0 1 1
1 1 0
Gambar 3. 9 Simbol dan tabel kebenaran gerbang logika NAND
Untuk ungkapan persamaan Boole gerbang NAND diberikan pada
persamaan 3.6 berikut ini.
. = 3. 6
3.5 Gerbang NOR
Dari namanya kita dapat memeri tafsiran bahwa gerbang NOR adalah sama
dengan Not OR atau gerbang OR yang diberi tambahan NOT pada keluarannya.
Seperti halnya gerbang NAND, logika NOT pada gerbang NOR dilambangkan
dengak lingkaran yang terletak pada kaki keluaran gerbang. Berdasarkan tabel
kebenaran yang diberikan dalam tabel pada Gambar 3. 10 kita dapat

26
BAB 3 GERBANG LOGIKA
mengidentifikasi bahwa keluaran gerbang NOR ini berkebalikan dengan keluaran
gerbang OR ata dengan kata lain keluaran (output) gerbang NOR merupakan
inversi dari gerbang OR.
Masukan Keluaran
A B Y
0 0 1
1 0 0
0 1 0
1 1 0
Gambar 3. 10 Simbol dan tabel kebenaran gerbang logika NOR
Tanda negasi yang merepresentasikan opearsi inversi terlihat pada ungkapan
persamaan Boole gerbang NOR seperti yang diberikan pada persamaan 3.7 berikut.
+ = 3. 7
3.6 Gerbang XOR
Gerbang XOR atau dikenal dengan istilah Exclusive OR memberikan
keluaran yang bernilai 1 apabila salah satu masukan mempunyai nilai yang
berbeda. Sedangkan keluaran akan bernilai 0 jika semua sinyal masukan yang
diberikan mempunyai nilai yang sama baik itu sama-sama 0 atau sama-sama 1.
Selengkapnya kombinasi nilai masukan dan nilai keluaran gerbang XOR dapat
dilihat dalam tabel pada Gambar 3. 11.
Masukan Keluaran
A B Y
0 0 0
1 0 1
0 1 1
1 1 0
Gambar 3. 11 Simbol dan tabel kebenaran gerbang logika XOR
Ungkapan persamaan Boole untuk gerbang XOR diberikan dalam persamaan
3.8 berikut ini.

27
BAB 3 GERBANG LOGIKA
⨁ = 3. 8
Soal-soal latihan (Tokheim, 1994):

28
BAB 4 RANGKAIAN LOGIKA
Dalam bab sebelumnya kita telah memberikan gambaran tentang 6 jenis
gerbang logika dasar yang menjadi dasar dalam berbagai rangkaian logika dalam
sebuah sistem digital. Dalam bab ini kita akan menggunakan pengertian yang sudah
kita pelajari tersebut untuk membahas rangkaian logika yang tersusun atas
beberapa gerbang logika baik yang sejenis maupun berbeda jenis. Untuk dapat
menggambarkan sebuah rangkaian gerbang logika, dalam bab ini kita juga akan
menjelaskan tentang aljabar Boole dan bagaimana metode untuk menyerhanakan
persamaan tersebut sehingga kita dapat memberikan alternatif rangkaian dengan
menggunakan gerbang berbeda atau membuat rangkaian yang lebih sederhana
dengan fungsi yang sama.
4.1 Gerbang kombinasi
Sebuah rangkaian gerbang logika dapat disusun dari beberapa jenis gerbang
logika baik sejenis maupun berbeda jenis. Dalam sub-bab ini diberikan contoh-
contoh dan penjelasan kombinasi gerbang logika untuk membentuk suatu fungsi
tertentu. Sebagai contoh kita bisa membuat kombinasi gerbang AND dan gerbang
NOT. Seperti telah disinggung sebelumnya, gerbang NAND pada prinsipnya
merupakan kombinasi gerbang AND dan NOT. Sebagai ilustrasi perhatikan
Gambar 4. 1 berikut ini.
identik dengan
Gambar 4. 1. Kombinasi gerbang AND dan NOT ekuivalen dengan NAND
Pada gambar sebelah kiri masukan sinyal A dan B pada gerbang AND akan
menghasilkan keluaran = . yang selanjutnya akan menjadi masukan pada
gerbang NOT dan menghasilkan keluaran = . . Persamaan keluaran dari
gerbang NOT terakhir ini tidak lain adalah keluaran gerbang NAND seperti
ditunjukkan pada Gambar 4. 1 sebelah kanan.

29
BAB 4 RANGKAIAN LOGIKA
4.2 Aljabar Boole
Aljabar Boole adalah sebuah ungkapan untuk menuangkan hubungan
masukan dan keluaran dalam gerbang logika dan juga dalam suatu rangkaian logika
ke dalam bentuk persamaan matematik. Pada dasarnya hukum-hukum dalam
aljabar Boole didasari oleh ungkapan Boole untuk gerbang-gerbang logika AND,
OR, dan NOT. Berikut adalah hubungan masukan dan keluaran pada gerbang-
gerbang logika tersebut sesuai dengan ungkapan Boole.
Gerbang AND Gerbang OR Gerbang NOT
0 . 0 = 0 0 + 0 = 0 0 = 1
0 . 1 = 0 0 + 1 = 1 1 = 0
1 . 0 = 0 1 + 0 = 1
1 . 1 = 1 1 + 1 = 1
Beberapa operasi dasar dalam aljabar Boole bersesuaian dengan ungkapan-
ungkapan di atas. Teorema-teorema yang dipakai dalam aljabar boole dapat
dianalogikan dengan ungkapan dasar dari gerbang-gerbang logika tersebut di atas.
Berikut ini adalah beberapa teorema dasar dalam aljabar Boole.
Hukum Dasar
Gerbang AND Gerbang OR Gerbang NOT A.0 = 0 A + 0 = A A = 1 A.1 = A A + 1 = 1 A.A = A A + A = A A.A = 1 A + A = 1
Hukum komutasi
Q = A . B . C = C . A . B = C . B . A 4. 1
Q = A + B + C = C + A + B = C + B + A 4. 2
Hukum asosiasi
Q = A . (B . C) = (A . B) . C 4. 3
Q = A + (B + C) = (A + B) + C 4. 4
Hukum distribusi
(A . B) + (A . C) = A . (B + C) 4. 5
(A + B) . (A + C) = A + (B . C) 4. 6

30
BAB 4 RANGKAIAN LOGIKA
Hukum De Morgan
Q= . = + 4. 7
Q= + = . 4. 8
4.3 Map Karnaugh
Membuat penyederhanaan sebuah rangkaian logika dengan menggunakan
aljabar Boole seringkali sulit dilakukan. Bahkan solusi dari penyederhanaan
ungkapan Boole terkadang dianggap sudah paling edrhana padahal sebenarnya
masih bisa dibuat menjadi lebih sederhana. Map (peta) Karnaugh adalah sebuah
metode yang sederhana dan tidak berbelit-belit untuk menghasilkan sebuah
ungkapan Boole yang ringkas dari suatu rangkaian digital.
Map Karnaugh menggunakan metode pengelompokan dengan tabel
kebenaran dua dimensi yang akhirnya mampu menghilangkan beberapa variabel
yang ada dalam sebuah persamaan logika dalam aljabar Boole. Setiap “cell” dalam
map Karnaugh diberi label yang mencerminkan bahwa setiap cell merupakan satu
susunan kombinasi yang mungkin dari seluruh mariabel masukan. Kita dapat juga
mengatakan bahwa jumlah cell dalam map Karnaugh adalah 2n dimana n adalah
jumlah variabel masukan masukan dalam rangkaian logika yang akan
disederhanakan.
(a) (b)
Gambar 4. 2. (a) Rangkaian gerbang logika 2 masukan dan (b) jumlah cell yang mungkin pada map Karnaugh untuk penyederanaan rangkaian.
Sebagai contoh kita lihat rangkaian gerbang logika seperti tampak pada
Gambar 4. 2. Ada 2 variabel masukan dalam sistem digital tersebut yaitu A dan B.
Dengan demikian jumlah cell yang mungkin ada dalam map Karnaugh adalah 22
ata sama dengan 4 buah cell yaitu AB, AB, AB, dan AB.

31
BAB 4 RANGKAIAN LOGIKA
Sekarang marilah kita melakukan analisis rangkaian pada Gambar 4. 2
dengan menuliskan keluaran Y dalam ungkapan prsamaan Boole.
Y = E + F
Y = A. B + A. D
= . + . , karena = 4. 9
Berdasarkan ungkapan persamaan keluaran di atas kita dapat melihat bahwa ada
dua suku dalam persamaan yaitu suku pertama adalah . dan suku kedua adalah . . Selanjutnya kita mengisikan nilai 1 pada cell yang bersesuaian dengan setiap
suku pada persamaan tersebut dengan ketentuan tanda “negasi” merepresentasikan
angka 0. Sebagai contoh suku akan memberikan nilai 1 pada cell A=1 dan cell
B=1 sedangkan suku . memberikan nilai 1 pada cell A=1 dan cell B=0. Dengan
demikian cell yang bernilai 1 adalah cell A=1, B=1 dan cell A=1, B=0 atau tampak
pada Gambar 4. 3 berikut ini.
(a) (b)
Gambar 4. 3. Map Karnaugh untuk rangkaian gerbang logika pada Gambar 4. 2.
Untuk menyederhanakan persamaan keluaran dengan tabel yang sudah terisi
seperti pada Gambar 4. 3 (a) di atas, kita melakukan pengelompokan cell yang
mempunyai nilai sama. Dalam setiap kelompok, cell nya harus berdekatan dalam
satu baris atau satu kolom dan jumlah cell haruslah sama dengan 2i dengan i adalah
bilangan bulat positif. Dari contoh di atas kita hanya dapat membuat satu kelompok
cell yang mempunyai nilai 1 seperti yang ditandai dengan lingkaran pada Gambar
4. 3 (b) di atas. Kalau kita perhatikan lingkaran yang menandai cell dengan nilai 1
berada pada kolom A=1. Hal ini mencerminkan bahwa solusi persamaan rangkaian
logika yang dicari adalah sama dengan A. Dengan kata lain = . + . =A. Jadi apapun masukan yang diberikan pada B tidak akan mempengaruhi nilai
keluaran dari rangkaian tersebut.

32
BAB 4 RANGKAIAN LOGIKA
Untuk lebih memantapkan pemahaman, marilah kita tinjau satu contoh lagi
rangkaian logika dengan tiga masukan seperti terlihat pada Gambar 4. 4. Rangkaian
ini memiliki satu keluaran dari gerbang OR yang mempunyai 4 buah masukan.
Persamaan Boole dari keluaran rangkaian dapat kita tuliskan sebagai:
= + + + 4. 10
Penyederhanaan persamaan Boole untuk rangkaian pada Gambar 4. 4 dapat kita
lakukan dengan map Karnaugh yang mepunyai 23=8 cell karena rangkaian tersebut
mempunyai 3 variabel masukan yaitu A, B, dan C.
Gambar 4. 4. Rangkaian gerbang logika dengan tiga masukan.
Persamaan 4.10 yang merupakan ungkapan keuaran dari rangkaian logika
pada Gambar 4. 4 terdiri atas 4 suku yang akan menghasilkan nilai 1 pada 4 cell
dalam map Karnaugh seperti terlihat pada Gambar 4. 5 (a). Suku pertama
memberikan nilai 1 pada cell A=0, B=1, C=0, suku kedua emberikan nilai 1 pada
cell A=0, B=1, C=1, suku ketiga memberikan nilai 1 pada cell A=1, B=1, C=0, dan
suku keempat memberika nilai 1 pada cell A=1, B=1, C=1.
(a) (b)
Gambar 4. 5. Map Karnaugh untuk rangkaian gerbang logika pada Gambar 4. 4.

33
BAB 4 RANGKAIAN LOGIKA
Selanjutnya pengelompokan dilakukan dengan memperhatikan hasil pada
map Karnaugh. Karena kita mempunyai 4 atau 22 cell yang saling berdekatan maka
kita dapat mengelompokkannya menjadi satu seperti pada Gambar 4. 5 (b) yang
ditandai dengan lingkaran. Dari hasil pengelompokan ini kita dapat melihat bahwa
cell bernilai 1 untuk semua nilai A, semua nilai C dan hanya untuk B=1. Dari sini
kita dapat mengambil kesimpulan bahwa keluaran rangkaian gerbang dapat
dinyatakan dengan Y=B.
4.4 Konversi gerbang
Dalam menyusun suatu rangkaian dengan menggunakan gerbang-gerbang
logika, jumlah gerbang yang digunakan bukanlah satu-satunya pertimbangan yang
digunakan. Pertimbangan lainnya adalah jenis gerbang yang dipakai. Gerbang
logika umumnya dibentuk dalam sebuah rangkaian terpadu (IC) dimana sebuah IC
dapat terdiri dari beberapa gerbang logika sejenis. Misalnya sebuah IC 7400
mempunyai 4 buah gerbang NAND dua masukan di dalamnya. Apabila kita
membuat rangkaian dengan dua buah gerbang yang berbeda jenisnya maka kita
membutuhkan dua buah IC. Akan tetapi jika kita bisa membuat konversi gerbang
dari beberapa gerbang yang lain maka rangkaian tersebut mungkin dapat dibuat
dengan menggunakan sebuah IC saja dan hal ini akan lebih menghemat biaya.
Sebuah gerbang NAND atau NOR dapat didesain untuk dapat berfungsi
sebagai gerbang NOT dengan cara menggabungkan kedua masukannya menjadi
satu seperti di tunjukkan pada Gambar 4. 6.
Gambar 4. 6. Gerbang NAND dan NOR yang berfungsi sebagai gerbang NOT.
Kita juga dapat membuat konversi 3 buah gerbang NAND untuk dapat
berfungsi sebagai gerbang OR yang keluarannya dinyatakan dengan Y = A + B.
Menurut hukum De Morgan yang kedua (lihat persamaan 4.8) dinyatakan bahwa A + B = A. B dan dengan menegasikan kedua sisi kita mendapatkan A + B = A. B.
Suku persamaan sebelah kanan merupakan ungkapan Boole dari gerbang NAND

34
BAB 4 RANGKAIAN LOGIKA
dengan masukan “not A” dan “not B”. Dari Gambar 4. 6 kita dapat membuat
gerbang NOT dari gerbang NAND sehingga kita bisa merangkai 3 buah gerbang
NAND untuk menunjukkan keluaran A. B seperti terlihat pada Gambar 4. 7.
Gambar 4. 7. Fungsi gerbang OR yang didapat dari rangkaian 3 gerbang NAND.
Dengan metode konversi gerbang seperti ditunjukkan di atas, kita dapat
menyusun kembali rangkaian logika yang membetuhkan 3 macam gerbang (3 buah
IC) seperti diberikan pada Gambar 4. 2 hanya dengan menggunakan dua macam
gerbang (2 buah IC seperti terlihat pada Gambar 4. 8 di bawah ini.
Gambar 4. 8. Efisiensi penggunaan IC dengan konversi gerbang dari rangkaian logika yang diberikan pada Gambar 4. 2.
4.5 Half adder dan Full adder
Half adder atau penjumlah paruh adalah sebuah rangkaian logika untuk
menampilkan hasil penjumlahan dua bit bilangan biner. Rangkaian half adder
diberikan pada Gambar 4. 9 (a). Bilangan yang dijumlahkan diumpankan pada
masing-masing masukan yakni A dan B. Hasil penjumlahan ditunjukkan oleh
keluaran pada kaki S sedangkan nilai simpanan (carry) terlihat pada keluaran kaki
C. Kombinasi masukan yang mungkin dalam half adder dan variasi keluaran yang
dihasilkan ditunjukkan pada Gambar 4. 9 (b).

35
BAB 4 RANGKAIAN LOGIKA
Masukan Keluaran
A B S C
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
(a) (b)
Gambar 4. 9. Rangkaian half adder dan tabel kebenarannya.
Rangkaian half adder dapat juga dibentuk dengan menggunakan gerbang-
gerbang logika dasar AND, OR, dan NAND seperti terlihat pada Gambar 4. 10.
Bahkan half adder dapat dirangkai hanya dengan menggunakan satu jenis gerbang
logika yaitu NAND (Agarwal, 2006) seperti yang ditunjukkan pada Gambar 4. 11.
Gambar 4. 10. Rangkaian half adder yang disusun dari gerbang-grbang dasar.
Gambar 4. 11. Rangkaian half adder yang disusun hanya dari gerbang NAND.
Apabila dalam penjumlahan bilangan biner sudah terdapat simpanan dari
operasi penjumlahan sebelumnya maka rangkaian yang digunakan adalah
rangkaian full adder. Pada prinspnya rangkaian full adder merupakan gabingsan
dari dua rangkaian half adder dengan tambahan gerbang OR. Selengkapnya
rangkaian full adder dapat dilihat pada Gambar 4. 12 (a). Kombinasi sinyal
masukan yang mungkin dalam full adder dan sinyal keluaran hasil operasi dari
penjumlahan diberikan dalam tabel pada Gambar 4. 12 (b).

36
BAB 4 RANGKAIAN LOGIKA
Masukan Keluaran
A B Cin S C
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
(a) (b)
Gambar 4. 12. Rangkaian full adder dan tabel kebenarannya.
Soal-soal latihan:
1. Dengan menggunakan map Karnaugh sederhanakan beberapa persamaan Boole
berikut ini:
a. = D + A D + D + ABCD + ABCD + ABCD
b. = AB + AB + AB
c. = ABC + ABC + ABC + ABC
d. = AC + A. B + C + A. B. C + B
2.

37
BAB 4 RANGKAIAN LOGIKA
CONTOH SOAL! Sederhanakan fungsi logika berikut, gambarkan rangkaian gerbang logika dasar penyederhanaan,dan tabel kebenarannya! 1. F = AB' + A'B + AB (dua variabel 2. F = ABC + A'BC + AB'C (tiga variabel) 3. F = A'B'C'D + A'BC'D + A'B'CD (empat variabel) PENYELESAIAN ! 1. F = AB' + A'B + AB - Penyederhanaan dengan Aljabar F = AB' + A'B + AB = A(B'+B) + A'B = A(1) + AB = A + A'B = A + B - Gambar Rangkaian gerbang logika setelah disederhanakan :
- Tabel Kebenaran
2. F = ABC + A'BC + AB'C - Penyederhanaan dengan Aljabar F = ABC + A'BC + AB'C = (A+A') BC + AB'C = (1) BC + AB'C = BC + AB'C = (B+AB') C

38
BAB 4 RANGKAIAN LOGIKA
= (B+A) C = BC + AC - Gambar Gerbang Logika
- Tabel Kebenaran
3. F = A'B'C'D + A'BC'D + A'B'CD - Penyederhanaan dengan Aljabar F = A'B'C'D + A'BC'D + A'B'CD = AB'CD + ABC (D'+D) = AB'CD + ABC (1) = AB'CD + ABC = AC (B'D+B) = AC (B+D) = ABC + ACD - Gambar Gerbang Logika
- Tabel Kebenaran

39
BAB 4 RANGKAIAN LOGIKA

40
BAB 5 FLIP - FLOP
Sebelum membahas lebih jauh tentang flip-flop terlebih dahulu kita singgung
pengertian tentang rangkaian sekuensial. Dalam bab sebelumnya kita membahas
tentang rangkaian kombinatorial yang meliputi gerbang logika dasar, gerbang
kombinasi dan rangkaian logika yang mana keluaran dari rangkaian tergantung
pada kondisi masukan atau input yang diberikan pada saat itu. Kondisi sinyal
masukan sebelumnya tidak memberikan pengaruh apa-apa terhadap sinyal
keluaran. Hal ini karena rangkaian gerbang logika yang telah dibahas di depan
tidak memiliki unsur penyimpan (memory).
Selanjutnya pembahasan dalam bab ini difokuskan pada rangkaian sekuensial
yaitu sebuah rangkaian logika yang sinyal keluarannya tidak hanya tergantung pada
kondisi sinyal masukan yang diberikan saat itu tetapi juga dipengaruhi atau mampu
mengenali (mengingat) kondisi sinyal sebelumnya (Agarwal, 2006). Agar sebuah
rangkaian logika mampu mengenali kondisi masukan sebelumnya atau mempunyai
unsur pengingat maka rangkaian didesain agar sinyal keluaran diumpanbalikkan ke
salah satu masukan. Rangkaian sekuensial dikelompokkan menjadi dua kategori
yaitu (Mano and Ciletti, 2013):
1. Rangkaian sekuensial sinkron atau “Synchronous (clocked) sequential circuits”
yaitu rangkaian yang bekerja secara periodik dan dikontrol oleh suatu pulsa
detak (clock).
2. Rangkaian sekuensial tak sinkron atau “Asynchronous (unclocked) sequential
circuits” merupakan rangkaian yang keluarannya tidak mengalami perubahan
regular berdasarkan waktu tetapi perubahan keluaran akan terjadi saat ada
perubahan masukan yang diberikan.
Pada rangkaian sekuensial sinkron, perubahan akan terjadi dalam rangkaian
bila ada transisi clock yang aktif baik itu transisi (tepi) positif maupun transisi
(tepi) negatif. Transisi positif yaitu perubahan clock dari 0 ke 1 dan sebaliknya
transisi negatif adalah perubahan clock dari 1 ke 0. Contoh rangkaian sekuensial

41
BAB 5 FLIP - FLOP
sinkron adalah flip-flop, register, dan counter. Dalam bab ini kita hanya membahas
flip-flop, sedangkan register dan counter akan kita bahas pada bab berikutnya.
Flip-flop adalah rangkaian digital yang digunakan untuk menyimpan satu bit
secara semi permanen sampai ada suatu perintah untuk menghapus atau mengganti
isi dari bit yang disimpan. Prinsip dasar dari flip-flop adalah suatu komponen
elektronika dasar seperti transistor, resistor dan dioda yang dirangkai menjadi suatu
gerbang logika yang dapat bekerja secara sekuensial. Nama lain dari flip-flop
adalah multivibrator bistabil. Ada berbagai jenis flip-flop ditinjau dari beberapa
aspek namun pada penulisan ini yang kami bahas adalah flip-flop yang ditinjau
dari cara kerjanya yang terdiri dari Latch, flip-flop RS, flip-flop D, flip-flop JK,
flip-flop T, dan ‘Preset and Clear’.
5.1 Latch (memori satu bit)
Latch merupakan rangkaian dasar dari flip-flop yang tersusun dari dua buah
gerbang NOR atau gerbang NAND satu masukan seperti tampak pada Gambar 5. 1.
Keluaran dari setiap gerbang diumpan balikkan ke dalama masukan gerbang yang
lainnya. Dengan demikian keluaran dari kedua gerbang selalu berada pada keadaan
yang berbeda dan oleh karenanya disimbolkan dengan Q dan Q yang
mengindikasikan bahwa keluaran Q meruapakan inversi atau negasi dari Q. Jika q
bernilai 1 maka Q akan bernilai 0 dan sebaliknya.
(a) (b)
Gambar 5. 1. Rangkaian Latch yang tersusun dari gerbang NOR and NAND
Latch hanya mempunyai dua keadaan stabil sehingga sering pula disebut
dengan rangkaian bistabil (bistable circuit). Ketika rangkaian diberi masukan A=1
(lihat Gambar 5. 1) maka nilai keluaran Q=0. Selanjutnya keluaran Q
diumpanbalikkan ke masukan B sehingga B juga bernilai 0 dan keluaran Q=1
karena merupakan inversi dari B. Kaki keluaran Q dihubungkan dengan masukan A

42
BAB 5 FLIP - FLOP
sehingga A bernilai 1 yang merupakan nilai awal. Dengan demikian kondisi ini
sudah tidak berubah atau dalam kondisi stabil dan informasi keluaran Q=0 terkunci
(Latched) dalam rangkaian.
Kondisi stabil yang lain juga dapat tercapai ketika masukan A diberi nilai 0
dan keluaran Q bernilai 1. Selanjutnya kondisi stabil dalam rangkaian ini
menyimpan informasi sinyal keluaran Q=1. Kondisi stabil dalam rangkaian latch
tidak mungkin tercapai apabila kedua masukan A dan B memiliki nilai yang sama
baik sama-sama 0 atau sama-sama 1.
5.2 Flip-flop S-R
Seperti telah disebutkan di atas bahwa rangkaian dasar flip-flop adalah
rangkaian latch. Salah satu dari jenis flip-flop adalah flip-flop SR. Flip-flop ini
mempunyai dua masukan (S dan R) dan dua keluaran (Q dan Q), di mana salah satu
keluarannya (Q) berfungsi sebagai komplemen dari keluaran yang lain (Q). Flip-
flop ini disebut juga rangkaian dasar untuk membangkitkan sebuah variabel beserta
komplemennya (Even and Medina, 2012; Muis, 2012). Flip-flop SR dapat dibentuk
dari kombinasi empat gerbang NAND atau kombinasi dua gerbang NOR seperti
pada Gambar 5. 2.
(a) (b)
R S Q Kondisi
0 0 Q0 Tidak berubah
0 1 1 Set
1 0 0 Reset
1 1 . Invalid
(c)

43
BAB 5 FLIP - FLOP
Gambar 5. 2. Rangkaian S-R Flip-flop dan tabel kebenarannya
Tabel kebenaran untuk rangkaian flip-flop SR diberikan dalam tabel pada
Gambar 5. 2 (c). Dari tabel tersebut dapat dilihat bahwa keluaran akan bernilai 1
(set) jika nilai masukan S=1 dan keluaran akan bernilai 0 (reset) jika masukan R
bernilai 1. Dari hasil ini maka rangkaian flip-flop SR disebut juga dengan
rangkaian ‘set’ dan ‘reset’.
Selanjutnya apabila kedua masukan S dan R diberi nilai 0 maka nilai
keluaran tidak akan terpengaruh dan tetap pada kondisi awal atau nilainya tetap
tidak berubah seperti nilai semula (Q0). Akan tetapi jika kedua masukan S dan R
diberi nilai 1 maka keluaran akan menjadi invalid dimana kedua keluaran nilainya
sama-sama 0. Padahal nilai Q dan Q harus selalu berada pada keadaan yang
berbeda karena yang satu merupakan komplemen yang lain.
Gambar 5. 3. Diagram pewaktuan SR Flip-flop
Untuk lebih memperjelas gambaran tentang hubungan sinyal masukan dan
keluaran pada rangkaian flip-flop SR, kita bisa perhatikan diagram pewaktuan
seperti diberikan pada Gambar 5. 3. Mula-mula sinyal masukan S, R dan keluaran
Q pada kondisi 0. Ketika sinyal masukan S dikondisikan 1 maka sinyal keluaran Q
akan menjadi bernilai 1atau berada pada kondisi set. Keadaan ini tetap terjaga
meskipun sinyal masukan S berubah 0 karena jika kedua sinyal masukan sama
dengan 0 maka sinyal keluaran tetap pada posisi semula yang dalam hal ini bernilai
1. Selanjutnya kondisi sinyal keluaran akan berubah 0 ketika sinyal masukan R
bernilai 1 atau rangkaian pada kondisi reset. Terakhir nilai sinyal keluaran Q akan
kembali menjadi 1 pada saat sinyal masukan S diubah menjadi 1. Secara singkat

44
BAB 5 FLIP - FLOP
sekali lagi dapat dikatakan bahwa kondisi sinyal keluaran rangkaian flip-flop RS
tidak akan berubah bila kedua masukannya bernilai 0 dan keluaran Q bernilai 1
pada kondisi set (sinyal masukan S=1) serta keluaran Q bernilai 0 jika rangkaian di
reset (sinyal masukan R=1) dengan catatan kedua sinyal masukan tidak boleh
sama-sama memiliki nilai 1.
Flip-flop S-R terdetak (Clocked)
Flip-flop SR seperti yang telah dibahas di atas dalam prakteknya jarang
dipakai karena tidak tidak sinkron ketika digabung dengan flip-flop lain yang
umumnya menggunakan clock (detak) dalam masukannya sebagai pengontrol
sinyal keluaran. Untuk itu didesain sebuah flip-flop SR yang diberi clock pada
masukannya seperti terlihat pada Gambar 5. 4. Clock akan aktif ketika berada pada
kondisi berlogika tinggi atau bernilai 1.
Clock R S Q Kondisi
0 x x Q0 Tidak berubah
1 0 0 Q0 Tidak berubah
1 0 1 1 Set
1 1 0 0 Reset
1 1 1 . Invalid
Gambar 5. 4. Rangkaian SR flip-flop terdetak dan tabel kebenarannya

45
BAB 5 FLIP - FLOP
Gambar 5. 5. Diagram pewaktuan SR Flip-flop terdetak transisi tepi positif
5.3 Flip-flop D
Nama flip-flop ini berasal dari Delay. Flip-flop ini mempunyai hanya satu
masukan, yaitu D. Jenis flip-flop ini sangat banyak dipakai sebagai sel memori
dalam komputer. Pada umumnya flip-flop ini dilengkapi dengan masukan clock
(pemicu) seperti ditunjukkan pada Gambar 5. 6. Keluaran flip-flop D akan
mengikuti apapun keadaan D pada saat clock aktif atau clock dibuat berlogika 1.
Apabila masukan D berubah sedangkan kondisi clock pada posisi tidak aktif
(berlogika 0) maka nilai keluaran tidak akan terpengaruh dan tetap seperti keadaan
sebelumnya (Q0). Yang dimaksud dengan Q0 adalah keadaan keluaran Q tepat
sesaat sebelum kondisi clock berubah menjadi 0.
Clock D Q
0 0 1/0 0/1
0 1 1/0 0/1
1 0 0 1
1 1 .1 0
Gambar 5. 6. Rangkaian D Flip-flop dan tabel kebenarannya
Berdasarkan pada tabel kebenaran untuk flip-flop D, kita dapat melakukan
analisis pada diagram waktu seperti yang ditunjukkan pada Gambar 5. 7.

46
BAB 5 FLIP - FLOP
Gambar 5. 7. Diagram pewaktuan D Flip-flop
5.4 Flip-flop J-K
Dari uraian subbab-subbab sebelumnya dapat dilihat bahwa dasar dari semua
flip-flop adalah flip-flop RS. JK Flip-flop merupakan rangkaian flip-flop yang
dibangun untuk megantisipasi keadaan terlarang pada flip-flop S-R. Dalam
prakteknya, ada kalanya perlu merealisasikan flip-flop tertentu daripada flip-flop
yang tersedia, misalnya flipflop yang dibutuhkan tidak tersedia atau dari serpih
(chip) flip-flop yang digunakan masih ada sisa flip-flop dari jenis lain yang belum
termanfaatkan. Sebagaimana diuraikan di depan, flip-flop D dapat dibangun dari
flip-flop JK dengan memberikan komplemen J sebagai masukan bagi K. Flip-flop
D yang disusun dari flip-flop JK.

47
BAB 5 FLIP - FLOP
J K Q
0 0 1/0 0/1
0 1 0 0
1 0 1 0
1 1 toggle toggle
Gambar 5. 8. Rangkaian JK Flip-flop dan tabel kebenarannya
Gambar 5. 9. Diagram pewaktuan JK Flip-flop transisi tepi positif
Master Slave JK Flip-flop
Gambar 5. 10. Diagram pewaktuan Master Slave JK Flip-flop transisi tepi negatif
5.5 Flip-flop T
T Flip-flop merupakan rangkaian flip-flop yang dibangun dengan
menggunakan flip-flop J-K yang kedua inputnya dihubungkan menjadi satu, maka
akan diperoleh flip-flop yang memiliki watak membalik output sebelumnya jika

48
BAB 5 FLIP - FLOP
inputannya tinggi dan outputnya akan tetap jika inputnya rendah. Flip-flop T dapat
dibentuk dari flip-flop JK dengan menggabungkan masukan J dan K sebagai
masukan T. Perhatikan bahwa bila T=0 akan membuat J=K=0 sehingga keadaan
flip-flop tidak berubah. Tetapi bila T=1, J=K=1 akan membuat flip-flop beroperasi
secara toggle.
Gambar 5. 11. Rangkaian T Flip-flop dan tabel kebenarannya
Gambar 5. 12. Diagram pewaktuan T Flip-flop





![[Teknik Digital] SAP 1](https://static.fdokumen.com/doc/165x107/55cf984d550346d03396db8a/teknik-digital-sap-1-5624255d781ee.jpg)














