Filtragem Robusta para Sistemas Singulares Discretos no …& GOLDENBERG (1989)), sistemas de...

Filtragem Robusta para Sistemas Singulares

Discretos no Tempo

Jose Carlos Teles Campos

Tese apresentada a Escola de En-

genharia de Sao Carlos da Uni-

versidade de Sao Paulo, como

parte dos requisitos para ob-

tencao do tıtulo de Doutor em

Engenharia Eletrica

Orientador: Prof. Dr. Marco Henrique Terra

Co-orientador: Prof. Dr. Joao Yoshiyuki Ishihara

Sao Carlos2004

Dedicatoria

Dedico este trabalho a Clelia,

Marluce ( in memorian ), Mirela,

Monique e Maria Jose pelo

incentivo, cooperacao, renuncia,

compreensao, e oracoes.

Agradecimentos

• Ao Prof. Dr. Marco Henrique Terra, meu orientador, pela oportunidade conce-

dida, pela dedicacao, competencia, compreensao e amizade que me proporcionou

durante este perıodo de trabalho em comum;

• Ao Prof. Dr. Joao Yoshiyuki Ishihara, pela competencia, compreensao, amizade

e pelas inestimaveis contribuicoes, que facilitaram a execucao deste trabalho;

• A minha famılia, aos parentes e aos amigos pelo incentivo, pela compreensao,

pela confianca e pelas oracoes;

• Aos amigos do LASI, Adriano, Aline, Antonio Carlos, Arthur, Cleber Buosi,

Everaldo, Gılson, Guilherme, Karla, Luciana, Marcio, Renato Tinos e todos os

outros que nao foram aqui mencionados, pela ajuda e pelos momentos bem vividos

durante a minha permanencia em Sao Carlos;

• Aos colegas professores e funcionarios do Depto. de Engenharia Eletrica da UFC,

especialmente a Professora Laurinda, pela ajuda e pelo incentivo dado para a

realizacao deste trabalho;

• Aos professores e funcionarios do Depto. de Engenharia Eletrica da EESC-USP,

que de forma direta ou indireta, tiveram participacao neste trabalho e

• A CAPES pelo suporte financeiro fornecido para a realizacao deste trabalho.

Epıgrafe

“O Controle de nossos atos aliado a

persistencia otimiza os resultados”.

Maria Jose Loiola

Sumario

Lista de Figuras vi

Lista de Abreviaturas e Siglas vii

Resumo viii

Abstract ix

1 Introducao 1

1.1 Modelagem Singular (Descritora) . . . . . . . . . . . . . . . . . . . . . . 1

1.2 Exemplos Ilustrativos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1.3 Definicoes Preliminares . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

1.4 Modos Impulsivos e Causalidade . . . . . . . . . . . . . . . . . . . . . . 12

1.5 Organizacao Geral do Texto . . . . . . . . . . . . . . . . . . . . . . . . 13

1.6 Producao Academica Resultante deste Trabalho . . . . . . . . . . . . . 14

2 Estimativa Recursiva no Espaco de Estados 16

2.1 Estimativa Filtrada Recursiva no Espaco de Estados . . . . . . . . . . . 16

2.2 Estimativa Preditora Recursiva no Espaco de Estados . . . . . . . . . . 20

2.2.1 Estimativa Preditora - Corretora . . . . . . . . . . . . . . . . . . 24

2.2.2 Estimativa Filtrada Recursiva no Espaco de Estados em Funcaoda Estimativa Preditora . . . . . . . . . . . . . . . . . . . . . . . 27

3 Estimativa Filtrada Robusta BDU 28

3.1 O Problema de Mınimos Quadrados com Incertezas . . . . . . . . . . . . 28

3.2 Estimativa Filtrada Robusta . . . . . . . . . . . . . . . . . . . . . . . . 30

4 Estimativa Filtrada para Sistemas Singulares 41

4.1 Estimativa Filtrada para Sistemas Singulares . . . . . . . . . . . . . . . 41

4.2 Estimativa Robusta para Sistemas Singulares . . . . . . . . . . . . . . . 46

iv

Sumario v

4.3 Comparacao com a Estimativa Filtrada BDU . . . . . . . . . . . . . . . 53

4.4 Estimativa Suavizadora Robusta . . . . . . . . . . . . . . . . . . . . . . 57

4.5 Exemplo Numerico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

5 Estimativa Preditora para Sistemas Singulares 60

5.1 Estimativa Preditora Singular . . . . . . . . . . . . . . . . . . . . . . . 60

5.1.1 Estimativa Preditora - Corretora Singular . . . . . . . . . . . . . 66

5.2 Estimativa Preditora Robusta Singular . . . . . . . . . . . . . . . . . . . 70

5.2.1 Comparacao com a Estimativa Preditora Singular sem Robustez 76

5.2.2 Comparacao com a Estimativa Preditora Robusta BDU . . . . . 78

5.2.3 Estimativa Preditora - Corretora Robusta Singular . . . . . . . . 83

6 Matriz de Variancias para Sistemas Singulares 88

6.1 Variancia do Erro da Estimativa Otima . . . . . . . . . . . . . . . . . . 88

6.2 Variancia da Estimativa Otima Determinıstica . . . . . . . . . . . . . . 93

6.3 Aplicacao as Estimativas Robustas Singulares . . . . . . . . . . . . . . . 97

6.3.1 Aplicacao a Estimativa Filtrada Robusta Singular . . . . . . . . 100

6.3.2 Aplicacao a Estimativa Preditora Robusta Singular . . . . . . . . 102

6.4 Variancia do Erro de Estimativa do Filtro BDU . . . . . . . . . . . . . 105

7 Conclusoes e Continuidade do Estudo 112

A Alguns Resultados da Analise Matricial 117

A.1 Alguns Resultados de Analise Matricial . . . . . . . . . . . . . . . . . . 117

A.1.1 Lema da Inversao de Matrizes . . . . . . . . . . . . . . . . . . . . 117

A.1.2 Lemas Auxiliares . . . . . . . . . . . . . . . . . . . . . . . . . . . 119

B Modelagem SVD para Sistemas Singulares 125

Lista de Figuras

1.1 Circuito RLC (Exemplo 1.2.1.) . . . . . . . . . . . . . . . . . . . . . . . 3

1.2 Circuito equivalente de uma chave perfeita (Exemplo 1.2.2.) . . . . . . . 4

1.3 Circuito equivalente do modelo do transistor (Exemplo 1.2.3). . . . . . . 5

1.4 Circuito eletrico contendo resistor nao-linear (Exemplo 1.2.4.) . . . . . . 5

1.5 Exemplo de um sistema nao redutıvel ao espaco de estados - Curva de

Crescimento da Producao Agrıcola (Exemplo 1.2.5.) . . . . . . . . . . . 7

1.6 Robo manipulador com tres juntas (Exemplo 1.2.7.) . . . . . . . . . . . 8

1.7 Modelagem nao-causal da recuperacao de uma imagem (Exemplo 1.2.8.) 9

4.1 Filtros Descriptor Robusto (DR), Otimo, e de Maxima Verossimilhanca

(ML). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59

vi

Lista de Abreviaturas e Siglas

• ARMA - Modelo auto-regressivo de media movel (autoregressive moving average

model)

• BDU - Dados com incertezas limitadas (Bounded Data Uncertainties)

• DR - Filtro Robusto Descritor (Descriptor Robust Filter)

• ML - Maxima Verossimilhanca (Maximum Likelihood)

• SVD - Decomposicao em valores singulares (Singular Value Decomposition)

vii

Resumo

Esta tese apresenta novos algoritmos que resolvem problemas de estimativas filtrada,

suavizadora e preditora para sistemas singulares no tempo discreto usando apenas

argumentos determinısticos. Cada capıtulo aborda inicialmente as estimativas para

o sistema nominal e em seguida, as versoes robustas para o sistema com incertezas

limitadas. Os resultados encontrados podem ser aplicados tanto em sistemas invariantes

como variantes no tempo discreto, utilizando a mesma estrutura do filtro de Kalman.

Nos ultimos anos, uma quantidade significativa de trabalhos envolvendo estimati-

vas singulares foi publicada enfocando apenas a estimativa filtrada sob a justificativa

de que a estimativa preditora era de significativa complexidade quando modelada pelo

metodo dos mınimos quadrados. Por este motivo, poucos trabalhos, como NIKOUK-

HAH et al. (1992) e ZHANG et al. (1998), deduziram a estimativa preditora. Este

ultimo artigo apresentou tambem um algoritmo para a estimativa suavizadora, mas

usando o modelo de inovacao ARMA. No entanto, ate onde foi possıvel identificar,

nenhum trabalho ate agora resolveu o problema de estimativa robusta, considerando

incertezas nos parametros, para sistemas singulares.

Para a deducao das estimativas singulares robustas, esta tese tomou como base

SAYED (2001), que deduz o filtro de Kalman robusto com incertezas limitadas utili-

zando uma abordagem determinıstica, o chamado filtro BDU. Os filtros robustos para

sistemas singulares apresentados nesta tese, sao mais abrangentes que os apresentados

em SAYED (2001). Quando particularizados para o espaco de estados sem incertezas,

todos os filtros se assemelham ao filtro de Kalman.

Palavras–Chave: Sistemas Singulares Discretos no Tempo, Filtro de Kalman, Filtro

Robusto, Estimativas Filtrada e Preditora, Mınimos Quadrados Recursivos.

viii

Abstract

New algorithms to optimal recursive filtering, smoothed and prediction for general

time-invariant or time-variant descriptor systems are proposed in this thesis. The esti-

mation problem is addressed as an optimal deterministic trajectory fitting. This problem

is solved using exclusively deterministic arguments for systems with or without uncer-

tainties. Kalman type recursive algorithms for robust filtered, predicted and smoothed

estimations are derived.

In the last years, many papers have paid attention to the estimation problems of

linear singular systems. Unfortunately, all those works were concentrated only on the

study of filtering problems, for nominal systems. The predicted and smoothed filters

are more involved and were considered only by few works: NIKOUKHAH et al. (1992)

and ZHANG et al. (1998). ZHANG et al. (1998) had proposed a unified approach for

filtering, prediction and smoothing problems which were derived by using the projection

formula and were calculated based on the ARMA innovation model, but they had not

considered the uncertainties.

In this thesis it is applied for descriptor systems a robust procedure for usual state

space systems developed by SAYED (2001), called BDU filter. It is obtained a robust

descriptor Kalman type recursions for filtered, predicted and smoothed estimates. Con-

sidering the nominal state space, all descriptor filters developed in this work collapse to

the Kalman filter.

Keywords: Linear Systems, Descriptor Systems, Singular Systems, Robust Filter,

Kalman Filtering, State Estimation, Parametric Uncertainty, Discrete-time Systems,

Least-squares.

ix

Capıtulo 1

Introducao

O estudo da estimativa e do controle de sistemas descritores (tambem conhecidos

como sistemas singulares ou sistemas implıcitos) tem recebido significativa atencao na

literatura. Isto ocorre porque sistemas na formulacao descritora surgem naturalmente e

frequentemente nos processos de modelagem de sistemas economicos (LUENBERGER

(1977)), modelagem de imagens (HASAN & AZIM-SADJANI (1995)), pacotes de pro-

gramas de modelagem orientados a objetos (GERDIN et al. (2003)), robotica (MILLS

& GOLDENBERG (1989)), sistemas de potencia, circuitos eletricos, engenharia ae-

roespacial, processos quımicos, sistemas biologicos, analise de series temporais, etc.

Alem disso, a formulacao descritora e mais abrangente de modo que a modelagem no

espaco de estados convencional e um caso particular seu, daı ela ser chamada tambem

de sistema generalizado (VERGHESE et al. (1981)). Ha sistemas que nao podem ser

modelados no espaco de estados, mas facilmente modelados como um sistema descri-

tor (ZAGHLOUL & NEWCOMB (1986)). A seguir serao feitas consideracoes sobre a

conceituacao destes sistemas, definicoes principais e exemplos ilustrativos.

1.1 Modelagem Singular (Descritora)

Seja o sistema representado por

f(x(t), x(t), u(t), t

)= 0 (1.1)

1

CAPITULO 1. INTRODUCAO 2

e

g(x(t), u(t), y(t), t

)= 0 (1.2)

sendo x(t) o estado do sistema, u(t) a entrada de controle, y(t) a medida da saıda, f e

g sao funcoes vetoriais de x(t), x(t), u(t) e t com dimensoes apropriadas. Sistemas que

tem a formulacao (1.1) - (1.2) sao chamados de sistemas implıcitos ou singulares. Um

caso especial de (1.1) - (1.2) ocorre quando

E(t)x(t) = ϕ1

(x(t), u(t), t

)(1.3)

y(t) = ϕ2

(x(t), u(t), t

)(1.4)

sendo ϕ1, ϕ2 funcoes vetoriais de x(t), u(t) e t. A matriz E(t) normalmente e retangular.

Se ϕ1 e ϕ2 sao funcoes lineares de x(t) e u(t), a formulacao mais conhecida para este

sistema e

E(t)x(t) = A(t)x(t) +B(t)u(t) (1.5)

y(t) = C(t)x(t). (1.6)

Quando E(t) e nao singular, o sistema recai no espaco de estados convencional,

daı a outra denominacao para ele: sistema generalizado. De acordo com DAI (1989d),

os sistemas singulares foram mencionados pela primeira vez na literatura em 1973

(SINGH & LIU (1973)). Em varias publicacoes, os sistemas singulares sao chama-

dos tambem de sistemas no espaco de semi-estado, sistemas degenerados e sistemas

algebrico-diferenciais, por envolver equacoes algebricas e equacoes diferenciais. Na

proxima secao serao mostrados varios exemplos de sistemas singulares.


1.2 Exemplos Ilustrativos

Exemplo 1.2.1 O circuito RLC da Figura 1.1 e modelado pelas seguintes equacoes

Ldi(t)

dt= vL(t)

CdvC(t)

dt= i(t)

0 = vR(t)−Ri(t)

0 = vR(t) + vL(t) + vC(t) + vS(t). (1.7)

Escolhendo-se como saıda a tensao no capacitor tem-se entao

L 0 0 0

0 0 C 0

0 0 0 0

0 0 0 0

di(t)dt

dvL(t)dt

dvC (t)dt

dvR(t)dt

=

0 1 0 0

1 0 0 0

−R 0 0 1

0 1 1 1

i(t)

vL(t)

vC(t)

vR(t)

+

0

0

0

1

vS(t)(1.8)

y(t) =[

0 0 1 0]

i(t)

vL(t)

vC(t)

vR(t)

(1.9)

-

+

L

-v (t)sv (t)C

R

v (t)Lv (t)R

CI(t)

Figura 1.1: Circuito RLC (Exemplo 1.2.1.)

Os dois exemplos mostrados a seguir sao caracterısticos de sistemas com compor-


tamentos impulsivos.

Exemplo 1.2.2 Seja o circuito representativo de uma chave perfeita, conforme Figura

1.2, cuja equacao matricial e dada por

1 0

0 0

x2(t)

x1(t)

=

0 1

1 ε

x2(t)

x1(t)

, t ≥ 0 (1.10)

cuja solucao impulsiva e dada por

x2(t)

x1(t)

=

0

−x2(0−)δ(t)

, t ≥ 0.

+

-

t = 0

x1

x2 1 ε

Figura 1.2: Circuito equivalente de uma chave perfeita (Exemplo 1.2.2.)

Exemplo 1.2.3 Seja a Figura 1.3 a seguir que mostra a representacao mais simples

para o modelo de um transistor. A equacao descritora deste circuito e dada por

C 0

0 0

x(t) =

0 1

1 0

x(t) +

0

1

u(t), t ≥ 0 e (1.11)

y(t) =[

0 αR]x(t), (1.12)

sendo

x(t) =

vC(t)

iE(t)

.


+

--

+ R

V C

y

α

-

+

V R yvC

-

+

C

i E

Figura 1.3: Circuito equivalente do modelo do transistor (Exemplo 1.2.3).

Os exemplos 1.2.4 e 1.2.5 que serao mostrados a seguir caracterizam situacoes em

que a modelagem no espaco de estados nao se aplica, sendo portanto necessaria a

representacao descritora.

Exemplo 1.2.4 Seja o circuito RC da Figura 1.4, com a resistencia tendo carac-

terısticas nao lineares. A representacao matematica deste circuito e dada por

0 C 0

0 0 0

0 0 0

x(t) +

0 0 1

1 1 0

1 0 −3

x(t) +

0

0

i3R

=

0

1

0

u(t), t ≥ 0(1.13)

y(t) =[

0 1 0]x(t), (1.14)

sendo x(t) =[vTR vTC iTR

]T. Note que este modelo (1.13)-(1.14) esta na forma de

semi-estados. Porem pode-se mostrar que este circuito 1.4 nao pode ser representado

na forma de espaco de estados.

-+

R +

-

VR

CV Y

1

23

Figura 1.4: Circuito eletrico contendo resistor nao-linear (Exemplo 1.2.4.)


O exemplo a seguir trata do problema do crescimento da producao agrıcola.

Exemplo 1.2.5 A curva do crescimento da producao agrıcola e dada pela expressao

˙y(t)/y(t) = K(y∗ − y(t)) e pela funcao mostrada na Figura 1.5. A equacao de y(t)

e dada por y(t) = y∗ eKy∗(t−t∗)

1+eKy∗(t−t∗) . Da curva da funcao logıstica percebe-se tres regioes

distintas, sendo uma com crescimento exponencial, outra com crescimento linear e

outra com crescimento logarıtmico. Esta curva de crescimento da producao agrıcola e

solucao da seguinte equacao retangular singular

0 1 0 0 0 0 0 0 0

0 0 0 1 0 0 0 0 0

0 0 0 0 0 1 0 0 0

0 0 0 0 0 0 0 1 0

0 0 0 0 0 0 0 0 1

x(t)

=

−s1 −s11|α| − α 1 α α 0 0 0

a− 1 0 −a −a 1− aα 1 0 0 0

0 0 α− 1 0 −α −α 1|s2|

1 0

0 0 0 0 −1 0 1|s2|− 1 0 1

0 0 0 0 0 0 s2 − 1 −s2 0

x(t)

+[

0 0 0 0 (ω20.|α|.|a|)

]Tu, t ≥ 0 e (1.15)

y(t) =[|a|−1 1 0 0 0 0 0 0 0

]x(t). (1.16)

Os termos s1, s1, s2, α, a e ω0 estao definidos em BONILLA & MALABRE (2000).

O exemplo a seguir e um caso tıpico de sistema retangular que ocorre em controle

otimo.

Exemplo 1.2.6 (DAI (1989)) Considere o problema de controle otimo com restricao.

Deseja-se encontrar o valor otimo do vetor u(t) tal que uma funcao custo L(x(t), u(t))

seja otimizada, sendo

x(t) = Ax(t) +Bu(t)

e a equacao de restricao


0 0.2 0.4 0.6 0.8 1 1.2 1.40

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Figura 1.5: Exemplo de um sistema nao redutıvel ao espaco de estados - Curva deCrescimento da Producao Agrıcola (Exemplo 1.2.5.)

y(t) = Cx(t) +Du(t).

Re-escrevendo-se a equacao de estado e a de restricao em uma unica formulacao ma-

tricial, tem-se

I 0

0 I

0 0

x(t)

y(t)

=

A 0

0 0

C −I

x(t)

y(t)

+

B

0

D

u(t),

portanto uma nova formulacao para o problema consiste em se achar um valor otimo

de u(t) para este sistema singular tal que a funcao custo L(x(t), u(t)) seja otimizada.

Exemplo 1.2.7 Considere o modelo simplificado e linearizado de um braco de robo

com tres juntas usado para limpeza de grandes edifıcios, conforme Figura 1.6, com a

seguinte equacao Lagrangeana de movimento

M(θ(t)

)dθ2(t)

dt2+ C

(θ(t),

θ(t)

dt

)+G

(θ(t)

)= u+ F Tµ

ψ(θ(t)

)= 0. (1.17)

sendo θ(t) =[θ1(t) θ2(t) θ3(t)

]To vetor das posicoes das juntas, M(.) ∈ R

3×3 e

a matriz de inercia, u ∈ R3 e o vetor de torques aplicados nas juntas, C(., .) ∈ R

3 e o


vetor de forcas centrıfugas e de Coriolis e G(.) ∈ R3 e o vetor de forcas gravitacionais.

A funcao de restricao ψ e dada por

ψ(θ) =

l1cos(θ1) + l2cos(θ1 + θ2) + l3cos(θ1 + θ2 + θ3)− l

θ1 + θ2 + θ3

. (1.18)

F = ∂(ψ)∂(θ) , µ ∈ R

2 e o multiplicador de Lagrange e F Tµ e a forca de restricao genera-

lizada. Linearizando-se este sistema e escrevendo-o na forma Cartesiana, tem-se

M0δz +D0δz +K0δz = S0δu+ F T0 δµ

F0δz = 0. (1.19)

Seja x =[δz δz δµ

]Te u = δu, entao o sistema fica na seguinte forma descritora

I3 0 0

0 M0 0

0 0 0

x =

0 I3 0

−K0 −D0 F T0

F0 0 0

x+

0

S0

0

u. (1.20)

A

B

x

y

2− θ

3− θ

1

23

1θ

Figura 1.6: Robo manipulador com tres juntas (Exemplo 1.2.7.)


Exemplo 1.2.8 (HASAN & AZIM-SADJANI (1995)). Este exemplo trata de um pro-

blema de recuperacao de imagem. A Figura 1.7 apresenta uma regiao dita de suporte

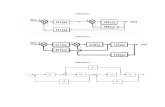
(ROS) de um sistema nao-causal representado pela seguinte equacao descritora

Exi+1 = Axi +Bui

zi = Cxi,

sendo

E =

1 0 0 0 0 0

0 1 0 0 0 0

0 0 1 0 0 0

0 0 0 1 0 0

0 0 0 0 0 0

0 0 0 0 0 0

, A =

0 0 1 0 0 0

0 0 0 1 0 0

0 0 0 0 1 0

0 0 0 0 0 1

ρ1+ρ2

0 −1 0 ρ1+ρ2

0

0 ρ1+ρ2

0 −1 0 ρ1+ρ2

,

B =

0 0 0 0 0 1

0 0 0 0 1 0

T

, C =

0 0 1 0 0 0

0 0 0 1 0 0

, xi =

zi−1

zi

zi+1

,

e E [zi−j,k−lzi,k] = ρ|j|+|l|, |ρ| < 1, sendo E [.] a esperanca matematica.

ROS

zi-p i+pziz

Figura 1.7: Modelagem nao-causal da recuperacao de uma imagem (Exemplo 1.2.8.)


1.3 Definicoes Preliminares

Estas definicoes foram retiradas das referencias (DAI (1989c)), (DAI (1989b)), (DAI

(1989d)), (LEWIS (1986)), (CAMPBELL (1982)), (ISHIHARA & TERRA (2001)),

(ISHIHARA & TERRA (2002)). Elas envolvem os sistemas contınuos e os sistemas

discretos no tempo. Tal como os exemplos apresentados na secao anterior, estas de-

finicoes foram incluıdas por motivacao didatica. Primeiro serao mostradas as definicoes

dos sistemas contınuos e em seguida, dos sistemas discretos.

Definicao 1.3.1 O sistema (1.5) - (1.6) com E ∈ Rn×n e regular se det(sE −A) 6= 0

para algum s ∈ C;

Definicao 1.3.2 O sistema regular (1.5) - (1.6) e estavel na dinamica finita se todas

as raızes de det(sE −A) = 0 estao no semi-plano esquerdo aberto;

Definicao 1.3.3 O sistema regular (1.5) - (1.6) e livre de impulsos se nao existir

nenhuma resposta impulsiva da forma

x(t) = xm(t) + ν0δ(t) + ν1δ(1)(t) + ν2δ

(2)(t) + . . .+ νkδ(k)(t),

sendo δ(t) a funcao de Dirac;

Definicao 1.3.4 O sistema regular (1.5) - (1.6) e impulso controlavel se e somente se

posto

E 0 0

A E B

= n+ posto(E);

Definicao 1.3.5 O sistema regular (1.5) - (1.6) e impulso observavel se e somente se

posto

E A

0 C

0 E

= n+ posto(E);

Definicao 1.3.6 O sistema regular (1.5) - (1.6) e detectavel na dinamica finita se

posto

sE −A

C

= n, Re(s) ≥ 0;

Definicao 1.3.7 O sistema regular (1.5) - (1.6) e S-observavel (fortemente observavel)

se e somente se posto

sE −A

C

= n, ∀s ∈ C;


Definicao 1.3.8 O sistema regular (1.5) - (1.6) e C-observavel ( completamente ob-

servavel ) se e somente se posto

sE −A

C

= n, ∀s ∈ C e posto

E

C

= n. Note

que C-observabilidade implica em S-observabilidade.

Para o caso dos sistemas discretos no tempo, valem as seguintes equacoes

Exi+1 = Axi +Bui (1.21)

yi = Cxi, (1.22)

com as respectivas definicoes,

Definicao 1.3.9 O sistema (1.21) - (1.22) com E ∈ Rn×n e regular se det(zE−A) 6= 0

para qualquer z ∈ C;

Definicao 1.3.10 O sistema regular (1.21) - (1.22) e estavel na dinamica finita se

todas as raızes de det(zE −A) = 0 estao no cırculo aberto de raio |z| < 1;

Definicao 1.3.11 O sistema regular (1.21) - (1.22) e causal ou nao antecipatorio se

grau(det(zE −A)) = posto(E);

A referencia (DAI (1989c)) define um sistema causal como sendo aquele em que x(i) em

qualquer instante i (i ≥ 0), pode ser determinado a partir de x(0) e de u(0), u(1) . . . u(i)

unicamente. Do contrario, ele e chamado de nao causal.

Definicao 1.3.12 O sistema regular (1.21) - (1.22) e controlavel na dinamica finita

se e somente se o posto

E 0 0

A E B

= n+ posto(E);

Definicao 1.3.13 O sistema regular (1.21) - (1.22) e observavel na dinamica finita se

e somente se o posto

zE −A

C

= n para ∀z ∈ C ;

Definicao 1.3.14 O sistema regular (1.21) - (1.22) e detectavel na dinamica finita se

o posto

zE −A

C

= n, |z| ≥ 1.


1.4 Modos Impulsivos e Causalidade

Em engenharia os impulsos podem causar danos ou ate a destruicao de equipamen-

tos. Os modos impulsivos e a causalidade podem ser melhor entendidos se for usada a

chamada forma de Weierstrass, que decompoe o sistema (1.5) - (1.6) em um sub-sistema

chamado de lento e um outro chamado de rapido. A forma de Weierstrass afirma que se

o sistema for regular entao existem duas matrizes Qw e Pw que decompoem o sistema

de forma que

x1(t) = A1x1(t) +B1u(t) (1.23)

Nx2(t) = x2(t) +B2u(t) (1.24)

y(t) = C1x1(t) + C2x2(t), (1.25)

sendo QwEPw =

In1 0

0 N

, QwAPw =

A1 0

0 In2

, QwB =

B1

B2

, x(t) =

Pw

x1(t)

x2(t)

, CPw =[C1 C2

]e n = n1 + n2. N e uma matriz nilpotente. A

solucao deste sistema usando-se a transformada de Laplace e dada por

x1(t) = exp(A1t)x1(0) +

∫ t

0[exp(A1(t− τ))]B1u(τ)dτ (1.26)

x2(t) = −

d−1∑

i=1

N ix2(0−)δ(i−1)(t)−

d−1∑

i=0

N iB2u(i)(t), (1.27)

sendo d o ındice de nilpotencia da matriz N , δ(t) e a funcao delta de Dirac, u(i)(t) e

a i-esima derivada de u(t), x1(t) e x2(t) sao chamados de semi-estados lento e rapido

respectivamente. Pode-se observar que os modos impulsivos podem aparecer em x2(t) se

Nx2(0−) 6= 0 ou se u(t) nao for diferenciavel. Pode-se concluir conforme (VERGHESE

et al. (1981)), que os modos impulsivos nao aparecerao em x2(t) se N = 0, que equivale

ao sistema nao ter polos no infinito.

Usando-se o mesmo procedimento de decomposicao para a formulacao discreta,

obtem-se a seguinte solucao para o sistema (1.21) - (1.22)

x1,i = Ai1x1,0 +

i−1∑

j=0

Ai−j−11 B1uj (1.28)


x2,i =

d−1∑

j=0

N jB2ui+j . (1.29)

A solucao x2,i e valida para sistemas no horizonte infinito. No caso de sistemas que

possuem condicao final, alem da inicial, a solucao x2,i e dada por

x2,i = N if−ix2,if −

if−i−1∑

j=0

N jB2ui+j , 0 ≤ i ≤ if , (1.30)

sendo x2,if a condicao final de x2,i. Pode-se observar pelas expressoes de x2,i, que

dependendo do valor de N , o sistema podera ser nao causal.

Finalmente, pode-se afirmar que tanto o problema dos modos impulsivos como o

da causalidade em aplicacoes de controle podem ser solucionados atraves do uso de

realimentacao de estado ou de saıda.

1.5 Organizacao Geral do Texto

A seguir e dada uma breve descricao de cada um dos capıtulos restantes.

• Capıtulo 2: Estimativa Recursiva no Espaco de Estados

Este capıtulo estuda as estimativas filtrada e preditora no espaco de estados

atraves do metodo dos mınimos quadrados recursivos, tal como em SAYED

(2001), mas sem a exigencia da matriz de ponderacao Q ser definida positiva,

apenas semi-definida positiva. Ele estuda tambem a estimativa preditora-corretora

e encontra a relacao que existe entre as expressoes de Pi+1|i+1 e Pi+1|i.

• Capıtulo 3: Estimativa Filtrada Robusta BDU

Este capıtulo apresenta a deducao detalhada do filtro robusto, denominado filtro

BDU (Bounded Data Uncertainties), apresentado em (SAYED (2001)). Este filtro

apresenta caracterısticas interessantes do ponto de vista de projeto. Uma destas

caracterısticas e que o intervalo do parametro de ajuste deste filtro e conhecido

a-priori, a partir dos parametros do sistema. Este filtro minimiza o erro de

estimativa para as maiores incertezas que aparecem no sistema, utilizando uma

abordagem determinıstica.

• Capıtulo 4: Estimativa Filtrada para Sistemas Singulares


Este capıtulo apresenta a estimativa filtrada singular inicialmente sem robustez

e depois com a inclusao da robustez nas matrizes E, F e H. Em seguida, ele

apresenta a comparacao desta estimativa com a estimativa filtrada robusta no

espaco de estados deduzida no artigo SAYED (2001).

• Capıtulo 5: Estimativa Preditora para Sistemas Singulares

Este capıtulo deduz inicialmente a estimativa preditora e a estimativa preditora-

corretora sem robustez para um sistema singular. Em seguida, ele estuda a esti-

mativa preditora robusta singular e faz comparacoes tanto com a estimativa predi-

tora singular sem robustez, como com a estimativa preditora no espaco de estados.

Finalmente ele apresenta a expressao da estimativa preditora-corretora robusta

singular.

• Capıtulo 6: Matriz de Variancias para Sistemas Singulares

Este capıtulo demonstra que as matrizes chamadas de auxiliares ao longo das

deducoes Pi+1|i+1 do Teorema 4.2.1 do Capıtulo 4, Pi+1|i do Teorema 5.2.1 do

Capıtulo 5, e Pi+1|i+1 do Teorema 3.2.1 do Capıtulo 3, sao as matrizes das

variancias dos erros das estimativas filtrada robusta singular, preditora robusta

singular e filtrada robusta no espaco de estados, respectivamente. Para se chegar

a estes resultados foi usado o Lema de (YU et al. (1995), que usa a estimativa

otima pelo metodo da maxima verossimilhanca (Maximum Likelihood - ML).

• Capıtulo 7: Conclusoes e Continuidade do Estudo

Este capıtulo relata os resultados das deducoes encontradas e faz sugestoes para

a continuidade desta pesquisa.

1.6 Producao Academica Resultante deste Trabalho

Esta tese gerou ate agora os seguintes artigos

1. J.C.T. Campos, J. Y. Ishihara & M. H. Terra (2004). “ Estimativa Recursiva

Otima para Sistemas Singulares Discretos no Tempo”. XV Congresso Brasileiro

de Automatica - CBA, Gramado-RS-Brasil, setembro, 2004.

2. J.Y.Ishihara, M.H. Terra & J.C.T. Campos (2004). “Robust Kalman Estimators

for Discrete-Time Descriptor Systems ”. Proc. of American Control Conference,


Boston, MA, June/July.

3. J.Y.Ishihara, M.H. Terra & J.C.T. Campos (2004). “Optimal Recursive Estima-

tion for Discrete-time Descriptor Systems”. Proc. of American Control Confe-

rence, Boston, MA, June/July.

Capıtulo 2

Estimativa Recursiva no Espaco

de Estados

Este capıtulo estuda as estimativas filtrada, preditora e preditora-corretora no

espaco de estados usando-se o metodo dos mınimos quadrados recursivo.

2.1 Estimativa Filtrada Recursiva no Espaco de Estados

Considere o sistema modelado no espaco de estados variante no tempo descrito por

xi+1 = Fixi + wi, i = 0, 1, ...

zi = Hixi + vi. (2.1)

Nesta secao considera-se o problema de se achar um algoritmo recursivo para a estima-

tiva filtrada. Esta estimativa pode ser obtida a partir de uma conveniente utilizacao

determinıstica do metodo dos mınimos quadrados. Seja um conjunto de estimativas

{x0|i, x1|i, ..., xi|i} e um conjunto de medidas conhecidas {z0, z1, ..., zi}. Fixando-se um

instante de tempo i e supondo que a estimativa filtrada xi|i ja foi encontrada com sua

correspondente matriz de variancias do erro Pi|i, pode-se encontrar uma nova estima-

tiva para xi+1 a partir de uma nova medida zi+1, encontrando-se a solucao otima da

funcao custo

Ji = minxi,xi+1

[∥∥xi − xi|i∥∥2

P−1i|i

+ ‖xi+1 − Fixi‖2Q−1

i

+ ‖zi+1 −Hi+1xi+1‖2R−1

i+1

](2.2)

16

CAPITULO 2. ESTIMATIVA RECURSIVA NO ESPACO DE ESTADOS 17

para i > 0 e

J0 = minx0

[‖x0‖

2P−1

0+ ‖z0 −H0x0‖

2R−1

0

], para i = 0, (2.3)

sendo Qi uma matriz de ponderacao para o ruıdo de estado e Ri uma matriz de pon-

deracao para o erro de medida.

Para se encontrar a solucao deste problema, sera utilizada a tecnica dos mınimos

quadrados regularizados cuja funcao custo e dada por

minxi

[xTi Qxi + (Ax− b)TW (Ax− b)], (2.4)

que tem como solucao (SAYED (2001))

x = [Q+ATWA]−1ATWb, (2.5)

sendo Q,W ≥ 0 tais que Q+ATWA e invertıvel.

Teorema 2.1.1 A estimativa otima filtrada xi|i pode ser obtida a partir do seguinte

algoritmo recursivo

Passo 0: (Condicoes Iniciais )

P0|0 :=(P−1

0 +HT0 R

−10 H0

)−1; (2.6)

x0|0 := P0|0HT0 R

−10 z0 (2.7)

Passo i: Atualize {xi|i, Pi|i} para {xi+1|i+1, Pi+1|i+1} do seguinte modo

Pi+1|i+1 :=((Qi + FiPi|iF

Ti

)−1+HT

i+1R−1i+1Hi+1

)−1(2.8)

xi+1|i+1 = Fixi|i + Pi+1|i+1HTi+1R

−1i+1(zi+1 −Hi+1Fixi|i). (2.9)

Prova: Escrevendo-se a funcao custo (2.2) na forma de blocos matriciais, tem-se


Quanto a condicao inicial, ela e obtida fazendo-se a derivada parcial da Equacao (2.3),

resultando em

∂J0

∂x0= −2xT0 P

−10 − 2(z0 −H0x0)

TR−10 H0 = 0

= xT0 P−10 − zT0 R

−10 H0 + xT0H

T0 R

−10 H0 = 0. (2.19)

Igualando a zero obtem-se a solucao mınima

x0|0 = (P−10 +HT

0 R−10 H0)

−1HT0 R

−10 z0. (2.20)

Definindo-se P0|0 = (P−10 +HT

0 R−10 H0)

−1, entao

x0|0 = P0|0HT0 R

−10 z0. (2.21)

�

2.2 Estimativa Preditora Recursiva no Espaco de Estados

Considere o sistema representado pela Equacao (2.1) e a funcao custo dada por

minxi,xi+1

{‖xi − xi|i−1‖

2P−1

i|i−1

+ ‖xi+1 − Fixi‖2Q−1

i

+ ‖zi −Hixi‖2R−1

i

}. (2.22)

Reescrevendo-se esta equacao na forma matricial como foi feito para o caso da estima-

tiva filtrada no espaco de estados, obtem-se

xi|i−1 − xi

xi+1

T

P−1i|i−1 0

0 0

xi|i−1 − xi

xi+1

+

(

Fi I

Hi 0

xi|i−1 − xi

xi+1

−

Fixi|i−1

Hixi|i−1 − zi

)T

Q−1i 0

0 R−1i

(.

).

(2.23)

Comparando-se esta expressao com a Equacao (2.4), como tambem foi feito para o caso

da estimativa filtrada, obtem-se as equivalencias


A←

Fi I

Hi 0

; b←

Fixi|i−1

Hixi|i−1 − zi

;

Q←

P−1i|i−1 0

0 0

;W ←

Q−1i 0

0 R−1i

;

cuja solucao e dada por (2.5).

Teorema 2.2.1 Suponha que e dada uma sequencia {z0, z1, . . .}. A estimativa predi-

tora otima xi+1|i resultante de (2.22) pode ser obtida a partir do algoritmo recursivo

Passo 0:

P0|−1 := P0 (2.24)

x0|−1 := x0 = 0 (2.25)

Passo 1: Atualize {Pi|i−1, xi|i−1} para {Pi+1|i, xi+1|i} da seguinte forma

Pi+1|i := Qi + FiPi|i−1FTi − FiPi|i−1H

Ti (Ri +HiPi|i−1H

Ti )−1HiPi|i−1F

Ti (2.26)

xi+1|i := Fixi|i−1 + FiPi|i−1HTi (Ri +HiPi|i−1H

Ti )−1(zi −Hixi|i−1). (2.27)

Prova : Comparando-se a Equacao (2.23) com a Equacao (2.5), segue que

xi|i−1 − xi|i

xi+1|i

=

P−1i|i−1 + F Ti Q

−1i Fi +HT

i R−1i Hi F Ti Q

−1i

Q−1i Fi Q−1

i

−1

×

F Ti Q−1i Fixi|i−1 +HT

i R−1i (Hixi|i−1 − zi)

Q−1i Fixi|i−1

. (2.28)

Explicitando-se o termo xi+1|i


xi+1|i =[

0 I]


−1i Fi +HT

i R−1i Hi F Ti Q

−1i

Q−1i Fi Q−1

i

−1

×



Q−1i Fixi|i−1

. (2.29)

Aplicando-se o lema da inversao de blocos matriciais, Lema A.1.1, ao bloco matricial

central, resulta

xi+1|i =[−D−1C(A−BD−1C)−1 D−1 +D−1C(A−BD−1C)−1BD−1

]

×

(F Ti Q−1i Fi +HT

i R−1i Hi)xi|i−1 −H

Ti R

−1i zi

Q−1i Fixi|i−1

(2.30)

ou

xi+1|i =[−(D − CA−1B)−1CA−1 (D − CA−1B)−1

]

×

(F Ti Q−1i Fi +HT


Ti R

−1i zi

Q−1i Fixi|i−1

. (2.31)

Entao

xi+1|i = (D − CA−1B)−1

(Q−1i Fixi|i−1 −CA

−1((F Ti Q

−1i Fi +HT


Ti R

−1i zi

)). (2.32)

Definindo Pi+1|i := (D − CA−1B)−1, entao

Pi+1|i =

(Q−1i −Q

−1i Fi(F

Ti Q

−1i Fi +HT

i R−1i Hi + P−1

i|i−1)−1F Ti Q

−1i

)−1

= Qi + Fi(P−1i|i−1

+HTi R

−1i Hi)

−1F Ti

= Qi + FiPi|i−1FTi − FiPi|i−1H

Ti (Ri +HiPi|i−1H

Ti )−1HiPi|i−1F

Ti .

(2.33)

Assim


2.2.1 Estimativa Preditora - Corretora

Esta secao trata da Estimativa Preditora - Corretora que e a relacao entre a esti-

mativa filtrada e a estimativa preditora no espaco de estados, dada pelo Lema 2.2.1 a

seguir.

Lema 2.2.1 A expressao para atualizacao no tempo da estimativa, no espaco de esta-

dos, e dada por

xi+1|i = Fixi|i. (2.40)

Prova: Da Equacao (2.28) do Teorema 2.2.1 segue que

xi|i−1 − xi|i =[I 0

]


−1i Fi +HT

i R−1i Hi F Ti Q

−1i

Q−1i Fi Q−1

i

−1

×



Q−1i Fixi|i−1

. (2.41)

Usando-se o lema da inversao de blocos matriciais, encontra-se

xi|i−1 − xi|i =[

(A−BD−1C)−1 −(A−BD−1C)−1BD−1]

×

(F Ti Q−1i Fi +HT


Ti R

−1i zi

Q−1i Fixi|i−1

(2.42)

ou

xi|i−1 − xi|i = (A−BD−1C)−1

((F Ti Q

−1i Fi +HT


Ti R

−1i zi

− BD−1Q−1i Fixi|i−1

). (2.43)

Sendo,

(A−BD−1C)−1 =(F Ti Q

−1i Fi +HT

i R−1i Hi + P−1

i|i−1 − FTi Q

−1i QiQ

−1i Fi

)−1

=(HTi R

−1i Hi + P−1

i|i−1

)−1. (2.44)

Capıtulo 3

Estimativa Filtrada Robusta

BDU

3.1 O Problema de Mınimos Quadrados com Incertezas

Considere o seguinte problema de custo quadratico otimo

minx

max{δA, δb}

[‖x‖2Q + ‖(A+ δA) x− (b+ δb)‖2W

](3.1)

para um sistema cujas incertezas nos parametros sao descritas por

[δA δb

]= H∆

[Ea Eb

], (3.2)

sendo

Q Q = QT > 0, matriz de ponderacao de regularizacao,

W W = W T ≥ 0, matriz de ponderacao para o erro de estimativa,

A matriz N × n conhecida,

b vetor N × 1 conhecido,

δA matriz de perturbacao da matriz nominal A,

δb vetor de perturbacao do vetor nominal b,

H,Ea, Eb matrizes conhecidas com dimensoes apropriadas,

∆ matriz arbitraria satisfazendo ‖∆‖ ≤ 1(contracao).

28

CAPITULO 3. ESTIMATIVA FILTRADA ROBUSTA BDU 29

O seguinte resultado e provado em SAYED (2001).

Teorema 3.1.1 O problema de otimizacao (3.1)-(3.2) tem uma unica solucao x. Esta

solucao e dada por

x =(Q+AT WA

)−1 (AT Wb+ λETa Eb

)(3.3)

sendo que as matrizes de ponderacao modificadas Q e W sao definidas como

Q := Q+ λETa Ea (3.4)

W := W +WH(λI −HTWH

)†HTW (3.5)

e o parametro escalar positivo λ e determinado a partir do seguinte problema de otimi-

zacao

λ := arg maxλ≥‖HTWH‖

G (λ) (3.6)

com

G(λ) := ‖x(λ)‖2Q + λ ‖Eax(λ)− Eb‖2 + ‖Ax(λ)− b‖2W (λ) (3.7)

e as funcoes auxiliares sao definidas por

x(λ) :=[Q(λ) +ATW (λ)A

]−1 [ATW (λ)b+ λETa Eb

](3.8)

Q(λ) := Q+ λETa Ea (3.9)

W (λ) := W +WH(λI −HTWH

)†HTW. (3.10)

Tem-se ainda que o valor do custo otimo resultante de (3.1) e igual a G(λ) e e dado

por

G(λ) =

1

x

T

λ ‖Eb‖2 −λETb Ea

−λETa Eb Q(λ)

1

x

+ (Ax− b)TW (λ)(Ax− b). (3.11)

�


3.2 Estimativa Filtrada Robusta

Considere o seguinte modelo com incertezas

xi+1 = (Fi + δFi) xi + (Gi + δGi)wi

zi = Hixi + vi[δFi δGi

]= Mi∆i

[Ef,i Eg,i

](3.12)

sendo {Mi, Ef,i, Eg,i} matrizes conhecidas e ∆i uma matriz arbitraria satisfazendo

‖△i‖ ≤ 1. Fixe um instante de tempo i. Suponha que sejam conhecidas

(i) a estimativa filtrada de xi: xi|i e

(ii) a estimativa filtrada de wi: wi|i = 0

sendo que a estimativa filtrada de uma variavel ai indica o valor previsto para esta

variavel dado o conhecimento que se tem ate o instante i. Considere que ocorra uma

atualizacao na medida, ou seja, e dada uma nova medida zi+1. Note que os valores

‘reais’ para as variaveis xi, wi e zi+1 que ocorrem no sistema em geral diferem dos

valores previstos pelo nosso conhecimento do sistema e das nossas estimativas. Assim,

pode-se definir os seguintes erros de previsao

ex,i := xi − xi|i

ew,i := wi − wi|i = wi

ey,i+1 := zi+1 −Hi+1xi+1 = vi+1.

Os erros de previsao de cada variavel indicam o nosso desconhecimento a respeito da

respectiva variavel. Assim, o fato do erro de previsao em relacao a variavel wi ser

a propria wi, ou seja, ew,i = wi, indica que neste modelo nao se conhece o valor de

wi. Da mesma forma, o fato de se ter ey,i = vi decorre de considerarmos o nosso

desconhecimento da saıda ser representada na forma de um sinal de ruıdo vi. O valor

exato dos erros de previsao sao desconhecidos mas pode-se supor que sejam conhecidas

matrizes de ponderacao para estes erros

(i) matriz de ponderacao para o erro de previsao do estado ex,i: Pi|i


(ii) matriz de ponderacao para o erro de previsao do ruıdo de estado ew,i: Qi

(iii) matriz de ponderacao para o erro de previsao da saıda ey,i+1: Ri+1.

As matrizes de ponderacao indicam o peso relativo das variaveis, uma em relacao as

outras. A dependencia em relacao a i indica que o peso relativo varia a cada instante

i. Estas matrizes sao usadas para definir uma ponderacao (custo) do efeito dos erros

de previsao

Ji :=∥∥xi − xi|i

∥∥2

P−1i|i

+ ‖wi‖2Q−1

i

+ ‖zi+1 −Hi+1xi+1‖2R−1

i+1. (3.13)

Este custo dos erros de previsao, Ji, incorpora a informacao adicional zi+1 e depende

de xi, wi e das incertezas δFi e δGi. Note ainda que as estimativas dadas xi|i e wi|i sao

exatamente a solucao otima do problema de minimizar em xi e wi o seguinte custo dos

erros de previsao sem a informacao zi+1

∥∥xi − xi|i∥∥2

P−1i|i

+ ‖wi‖2Q−1

i

. (3.14)

Com isto, pode-se propor como atualizacao das estimativas de xi e wi em face ao

conhecimento da saıda zi+1, a solucao otima {xi|i+1, wi|i+1} do seguinte problema

min-max quadratico

xi|i+1

wi|i+1

:= arg min{xi,wi}

max{δFi,δGi}

{∥∥xi − xi|i

∥∥2

P−1i|i

+ ‖wi‖2Q−1

i

+ ‖zi+1 −Hi+1xi+1‖2R−1

i+1}

(3.15)

s.a.

xi+1 = (Fi + δFi) xi + (Gi + δGi)wi

zi+1 = Hi+1xi+1 + vi+1[δFi δGi

]= Mi∆i

[Ef,i Eg,i

], ‖△i‖ ≤ 1.

Com a solucao {xi|i+1, wi|i+1} pode-se construir uma estimativa filtrada para xi+1

(atualizacao no tempo para a estimativa semelhante a atualizacao no tempo do estado

na equacao de estados)


xi+1|i+1 := Fixi|i+1 +Giwi|i+1 =[Fi Gi

]

xi|i+1

wi|i+1

. (3.16)

Note que o problema de otimizacao (3.15) pode ser resolvido via Teorema 3.1.1, e

assim, a estimativa (3.16) pode ser obtida para cada i. As expressoes das estimativas

podem ser apresentadas na forma de um algoritmo do tipo predicao-correcao, conforme

o seguinte teorema.

Teorema 3.2.1 (Filtro robusto na forma preditora - corretora): Considere as equacoes

de estado e de saıda

xi+1 = (Fi + δFi)xi + (Gi + δGi)wi

zi = Hixi + vi (3.17)

com as incertezas nas matrizes Fi e Gi modeladas como

[δFi δGi

]= Mi△i

[Ef,i Eg,i

], ‖△i‖ ≤ 1. (3.18)

Considere ainda que as matrizes de ponderacao Π0 > 0, Ri > 0 e Qi > 0 sejam

conhecidas. As estimativas dos estados podem ser calculadas recursivamente segundo o

seguinte algoritmo

Passo 0 (Condicoes iniciais): Faca

P0|0 := (Π−10 +HT

0 R−10 H0)

−1,

x0|0 := P0|0HT0 R

−10 z0.

Passo 1 : Se Hi+1Mi = 0, entao faca λi = 0. Caso contrario, determine λi no intervalo

λ > λl,i := ‖MTi H

Ti+1R

−1i+1Hi+1Mi‖ (3.19)

que minimiza G(λ) definido por (3.7) com as identificacoes (3.36)-(3.46).


Passo 2 : Se λi 6= 0, substituir {Qi, Ri+1, Pi|i, Gi, Fi} por

Q−1i = Q−1

i + λiETg,i

(I + λiEf,iPi|iE

Tf,i

)−1Eg,i (3.20)

Ri+1 = Ri+1 − λ−1i Hi+1MiM

Ti H

Ti+1 (3.21)

Pi|i =(P−1i|i + λiE

Tf,iEf,i

)−1(3.22)

= Pi|i − Pi|iETf,i(λ

−1i I + Ef,iPi|iE

Tf,i)

−1Ef,iPi|i (3.23)

Gi = Gi − λiFiPi|iETf,iEg,i (3.24)

Fi =(Fi − λiGiQiE

Tg,iEf,i

)(I − λiPi|iE

Tf,iEf,i

). (3.25)

Se λi = 0, faca

Qi = Qi, Ri+1 = Ri+1, Pi|i = Pi|i, Gi = Gi, e Fi = Fi.

Passo 3 : Atualize {xi|i, Pi|i} da seguinte maneira

xi+1|i = Fixi|i (3.26)

xi+1|i+1 = xi+1|i + Pi+1|i+1HTi+1R

−1i+1ei+1 (3.27)

ei+1 = zi+1 −Hi+1xi+1|i (3.28)

Pi+1|i = FiPi|iFTi + GiQiG

Ti (3.29)

Pi+1|i+1 = Pi+1|i − Pi+1|iHTi+1R

−1e,i+1Hi+1Pi+1|i (3.30)

Re,i+1 = Ri+1 +Hi+1Pi+1|iHTi+1. (3.31)

Prova: Primeiro note que o funcional Ji pode ser re-escrito como

Ji =

ex,i

wi

ey,i+1

T

P−1i|i 0 0

0 Q−1i 0

0 0 R−1i+1

ex,i

wi

ey,i+1

(3.32)

sendo definidos os seguintes erros de informacao

ex,i := xi − xi|i,

ey,i+1 := zi+1 −Hi+1xi+1. (3.33)

Substituindo-se xi+1 pela equacao (3.17) na equacao do erro ey,i+1, tem-se


ey,i+1 := zi+1 −Hi+1xi+1

= zi+1 −Hi+1[(Fi + δFi)xi + (Gi + δGi)wi]

= zi+1 −Hi+1[(Fi + δFi)ex,i + (Fi + δFi)xi|i + (Gi + δGi)wi]

= (zi+1 −Hi+1xi+1|i)−Hi+1δFixi|i − (Hi+1

[Fi Gi

]

+ Hi+1

[δFi δGi

])

ex,i

wi

. (3.34)

Desta forma, o funcional a ser otimizado Ji pode ser re-escrito seguindo o padrao do

Teorema 3.1.1

Ji =

xi − xi|i

wi

T

P−1i|i 0

0 Q−1i

xi − xi|i

wi

+

+ [(Hi+1

[Fi Gi

]+Hi+1

[δFi δGi

])

xi − xi|i

wi

− ((zi+1 −Hi+1Fixi|i)−Hi+1δFixi|i)]TR−1

i+1(.). (3.35)

Assim, pelo Teorema 3.1.1 valem as seguintes identificacoes

x ←−

ex,i

wi

=

xi − xi|i

wi

(3.36)

b ←− zi+1 −Hi+1Fixi|i (3.37)

A ←− Hi+1

[Fi Gi

](3.38)

δA ←− Hi+1Mi∆[Ef,i Eg,i

](3.39)

δb ←− −Hi+1Mi∆Ef,ixi|i (3.40)

Q ←−

P−1i|i 0

0 Q−1i

(3.41)

W ←− R−1i+1 (3.42)

H ←− Hi+1Mi (3.43)

Ea ←−[Ef,i Eg,i

](3.44)

Eb ←− −Ef,ixi|i (3.45)

∆ ←− ∆i. (3.46)


A solucao x :=

[xi|i+1 − xi|i

wi|i+1

]do problema min-max (3.15) e encontrada resolvendo a

equacao

(Q(λi) +ATW (λi)A)x = (ATW (λi)b+ λiETa Eb) (3.47)

sendo

Q(λi) = Q+ λiETa Ea

=

P−1i|i 0

0 Q−1i

+ λi

ETf,i

ETg,i

[Ef,i Eg,i

], (3.48)

W (λi) = W +WH(λiI −H

TWH)−1

HTW

=(Ri+1 − λ

−1i Hi+1MiM

Ti H

Ti+1

)−1=: R−1

i+1, (3.49)

e λi e o argumento que minimiza a funcao G(λ) conforme o Passo 1 do enunciado do

teorema. Fazendo-se as substituicoes requeridas, a Equacao (3.47) se escreve como�24 P−1i|i

0

0 Q−1i

35+ λi

24 ETf,i

ETg,i

35h Ef,i Eg,i

i+

24 FTi

GTi

35HTi+1R

−1i+1Hi+1

hFi Gi

i�×

24 xi|i+1 − xi|i

wi|i+1

35 =

24 FTi

GTi

35HTi+1R

−1i+1

�zi+1 −Hi+1Fixi|i

�− λi

24 ETf,i

ETg,i

35Ef,ixi|i. (3.50)

Note que xi|i esta presente nos dois lados da Equacao (3.50) e que0�λi

24 ETf,i

ETg,i

35h Ef,i Eg,i

i+

24 FTi

GTi

35HTi+1R

−1i+1Hi+1

hFi Gi

i1A24 xi|i

0

35 =

=

24 FTi

GTi

35HTi+1R

−1i+1Hi+1Fixi|i + λi

24 ETf,i

ETg,i

35Ef,ixi|i. (3.51)

Desta forma, (3.50) pode ser re-escrita como�24 P−1i|i

0

0 Q−1i

35+ λi

24 ETf,i

ETg,i

35h Ef,i Eg,i

i+

24 FTi

GTi

35HTi+1R

−1i+1Hi+1

hFi Gi

i�×

24 xi|i+1

wi|i+1

35 =

24 FTi

GTi

35HTi+1R

−1i+1zi+1 +

24 P−1i|i

0

0 Q−1i

3524 xi|i

0

35 . (3.52)

Como se deseja encontrar a estimativa filtrada xi+1|i+1 para xi+1 que se considera como

sendo dada por


xi+1|i+1 := Fixi|i+1 +Giwi|i+1 =[Fi Gi

]

xi|i+1

wi|i+1

,

multiplicando-se os dois lados de (3.52) por

[Fi Gi

]

P−1i|i 0

0 Q−1i

+ λi

ETf,i

ETg,i

[Ef,i Eg,i

]

−1

, (3.53)

obtem-se uma equacao em xi+1|i+1

(I +

hFi Gi

i0�24 P−1i|i

0

0 Q−1i

35+ λi

24 ETf,i

ETg,i

35h Ef,i Eg,i

i1A−1 24 FTi

GTi

35| {z }Pi+1|i

× HTi+1R

−1i+1Hi+1

)[Fi Gi

]

xi|i+1

wi|i+1

︸︷︷︸xi+1|i+1

=[Fi Gi

]

P−1i|i 0

0 Q−1i

+ λi

ETf,i

ETg,i

[Ef,i Eg,i

]

−1

F Ti

GTi

︸︷︷︸Pi+1|i

× HTi+1R

−1i+1zi+1

+hFi Gi

i�24 P−1i|i

0

0 Q−1i

35+ λi

24 ETf,i

ETg,i

35h Ef,i Eg,i

i�−124 P−1

i|i0

0 Q−1i

3524 xi|i

0

35| {z }Fixi|i

.

(3.54)

Com as variaveis auxiliares Pi+1|i, xi+1|i+1 e Fi definidas conforme apresentadas em

(3.54), entao pode-se escrever de maneira compacta

(I + Pi+1|iH

Ti+1R

−1i+1Hi+1

)xi+1|i+1 = Pi+1|iH

Ti+1R

−1i+1zi+1 + Fixi|i. (3.55)

Supondo-se que a matriz (I + Pi+1|iHTi+1R

−1i+1Hi+1) possua inversa, entao


Q(λi)−1 =

(

P−1i|i 0

0 Q−1i

+ λi

ETf,i

ETg,i

[Ef,i Eg,i

])−1

=

P−1i|i + λiE

Tf,iEf,i −λiE

Tf,iEg,i

λiETg,iEf,i Q−1

i + λiETg,iEg,i

−1

=

I −λiPi|iETf,iEg,i

0 I

Pi|i 0

0 Qi

I 0

−λiETg,iEf,iPi|i I

.

(3.61)

Na Equacao (3.61) foram definidas as variaveis auxiliares

Pi|i := (P−1i|i + λiE

Tf,iEf,i)

−1 (3.62)

e

Qi :=

(Q−1i + λiE

Tg,iEg,i − λ

2iE

Tg,iEf,i

(P−1i|i + λiE

Tf,iEf,i

)−1ETf,iEg,i

)−1

=

(Q−1i + λiE

Tg,i

(I − λiEf,i

(P−1i|i + λiE

Tf,iEf,i

)−1ETf,i

)Eg,i

)−1

=

(Q−1i + λiE

Tg,i

(I − λiEf,i

(I + λiPi|iE

Tf,iEf,i

)−1Pi|iE

Tf,i

)Eg,i

)−1

=

(Q−1i + λiE

Tg,i

(I − λiEf,iPi|iE

Tf,i

(I + λiEf,iPi|iE

Tf,i

)−1)Eg,i

)−1

=

(Q−1i + λiE

Tg,i

(I + λiEf,iPi|iE

Tf,i

)−1Eg,i

)−1

(3.63)

que fornecem exatamente as equacoes (3.22) e (3.20) do Passo 2 do algoritmo do teo-

rema. Com isto, das equacoes (3.54) e (3.63) obtem-se

Pi+1|i :=[Fi Gi

]

P−1i|i 0

0 Q−1i

+ λi

ETf,i

ETg,i

[Ef,i Eg,i

]

−1

F Ti

GTi

(3.64)

ou


Pi+1|i =[Fi Gi

] [I −λiPi|iE

Tf,iEg,i

0 I

] [Pi|i 0

0 Qi

] [I 0


] [FT

i

GTi

]

Pi+1|i =[Fi Gi − λiFiPi|iE

Tf,iEg,i

]

Pi|i 0

0 Qi

F Ti(Gi − λiFiPi|iE

Tf,iEg,i

)T

.

Definindo-se a variavel auxiliar Gi como em (3.24), tem-se Pi+1|i escrita na forma

compacta (3.30). Novamente, das equacoes (3.54) e (3.63) segue que

Fi :=[Fi Gi

]

P−1i|i 0

0 Q−1i

+ λi

ETf,i

ETg,i

[Ef,i Eg,i

]

−1

P−1i|i

0

=[Fi Gi

] [I −λiPi|iE

Tf,iEg,i

0 I

] [Pi|i 0

0 Qi

] [I 0


] [P−1

i|i

0

]

=[Fi Gi − λiFiPi|iE

Tf,iEg,i

]

Pi|i 0

0 Qi

P−1i|i

−λiETg,iEf,iPi|iP

−1i|i

=[Fi Gi

]

I

−λiQiETg,iEf,i

Pi|iP−1i|i

=(Fi − λiGiQiE

Tg,iEf,i

)Pi|i

(P−1i|i − λiE

Tf,iEf,i

)

=(Fi − λiGiQiE

Tg,iEf,i

)(I − λiPi|iE

Tf,iEf,i

)

que e exatamente a expressao encontrada em (3.25). Para a condicao inicial x0, pode-

se supor que se conhece uma estimativa x0|−1 = 0 juntamente com uma matriz de

ponderacao para o erro de previsao Π0 > 0. Dada uma medida z0, para qual se conhece

a matriz de ponderacao para o erro de previsao R0 > 0, pode-se definir um custo do

erro de previsao como

C0 :=∥∥x0 − x0|−1

∥∥2

Π−10

+ ‖z0 −Hx0‖2R−1

0. (3.65)

Com isto pode-se propor como estimativa inicial dada a informacao z0 como sendo a

solucao otima x0|0 que minimiza o funcional (3.65). Como

C0 = xT0(Π−1

0 +HTR−10 H

)x0 − 2xT0H

TR−10 z0 + zT0 H

TR−10 Hz0. (3.66)


Derivando C0 em relacao a x0, obtem-se facilmente que a solucao otima e dada por

x0|0 = (Π−10 +HT

0 R−10 H0)

−1HT0 R

−10 z0.

Pode-se ainda, de forma consistente com (3.30), definir P0|0 :=(Π−1

0 +HT0 R

−10 H0

)−1.

�

Observacao 3.2.1 : Uma expressao alternativa para Qi envolvendo uma inversa a

menos e dada por

Qi :=

Q−1i + λiE

Tg,iEg,i − λ

2iE

Tg,iEf,i

(P−1i|i + λiE

Tf,iEf,i

)−1

︸︷︷︸Pi|i

ETf,iEg,i

−1

=(Q−1i + λiE

Tg,i

[I − λiE

Tg,iEf,iPi|iE

Tf,i

]Eg,i

)−1.

Capıtulo 4

Estimativa Filtrada para

Sistemas Singulares

Neste capıtulo apresenta-se a estimativa filtrada singular com e sem a inclusao

de incertezas nas matrizes E, F e H. O filtro robusto singular e comparado com a

estimativa filtrada robusta no espaco de estados do filtro BDU apresentado no Capıtulo

3.

4.1 Estimativa Filtrada para Sistemas Singulares

Seja o sistema linear discreto estocastico descrito por

Ei+1xi+1 = Fixi + wi

zi = Hixi + vi (4.1)

sendo xi o vetor de estados de dimensao n× 1 e zi o vetor de saıda de dimensao m× 1.

Ei+1 e Fi sao matrizes com dimensoes p × n e Hi e uma matriz com dimensao m× n.

wi e vi sao vetores que tem media zero com dimensoes p × 1 e m × 1 e matrizes de

covariancias

41

CAPITULO 4. ESTIMATIVA FILTRADA PARA SISTEMAS SINGULARES 42

E{wkwTi } =

Qi > 0 se i = k

0 se i 6= k

E{vkvTi } =

Ri > 0 se i = k

0 se i 6= k(4.2)

E{wkvTi } = 0 para todos k e i

e o estado inicial x0 e gaussiano com media x0 e variancia P0 > 0, independente

de vi e de wi. O filtro de Kalman singular, pode ser obtido a partir da solucao de

um problema de otimizacao determinıstico que corresponde a formulacao original do

problema estocastico. Assumindo que no instante i tem-se uma estimativa a-priori

para o estado xi, xi|i, uma matriz de ponderacao definida positiva para o erro xi− xi|i,

denominada Pi|i e uma nova medida zi+1, entao pode-se estimar um novo valor para

xi, xi+1|i+1 a partir das solucoes dos seguintes funcionais, para i = 0

minx0

[xT0 P−10 x0 + (z0 −H0x0)

TR−10 (z0 −H0x0)] (4.3)

e para i > 0

minxi,xi+1

[(xi − xi|i)TP−1

i|i (xi − xi|i) + (zi+1 −Hi+1xi+1)TR−1

i+1(zi+1 −Hi+1xi+1)

+ (Ei+1xi+1 − Fixi)TQ−1

i (Ei+1xi+1 − Fixi)]. (4.4)

Com estas informacoes pode-se enunciar o seguinte teorema

Teorema 4.1.1 Suponha que

Ei

Hi

tem posto coluna pleno para todo i ≥ 0. A esti-

mativa otima filtrada xi|i de xi pode ser obtida a partir do seguinte algoritmo recursivo

Passo 0: (Condicoes Iniciais)

P0|0 :=(P−1

0 +HT0 R

−10 H0

)−1;

x0|0 := P0|0HT0 R

−10 z0. (4.5)

Passo i: Atualize {xi|i, Pi|i} para {xi+1|i+1, Pi+1|i+1} como segue


Pi+1|i+1 :=

(

Ei+1

Hi+1

T

Qi + FiPi|iFTi 0

0 Ri+1

−1

Ei+1

Hi+1

)−1

; (4.6)

xi+1|i+1 := Pi+1|i+1

Ei+1

Hi+1

T

Qi + FiPi|iFTi 0

0 Ri+1

−1

Fixi|i

zi+1

. (4.7)

Prova: Re-escrevendo-se o funcional da Equacao (4.4) na forma de blocos matriciais,

segue que

[(xi − xi|i)

T xTi+1

]

P−1i|i 0

0 0

xi − xi|i

xi+1

+

(

−Fi Ei+1

0 Hi+1

xi − xi|i

xi+1

−

Fixi|i

zi+1

)T

Q−1i 0

0 R−1i+1

(.

).

(4.8)

Comparando-se os termos desta equacao com a dos mınimos quadrados, Equacao (2.4),

valem as seguintes equivalencias

x ←

xi − xi|i

xi+1

b ←

Fixi|i

zi+1

Q ←

P−1i|i 0

0 0

A ←

−Fi Ei+1

0 Hi+1

W ←

Q−1i 0

0 R−1i+1

.

A solucao de (4.8) e dada por


x = [Q+ATWA]−1ATWb. (4.9)

O termo ATWA fica sendo

ATWA =

−FTi 0

ETi+1 HTi+1

Q−1i 0

0 R−1i+1

−Fi Ei+1

0 Hi+1

=

F Ti Q−1i Fi −F Ti Q

−1i Ei+1

−ETi+1Q−1i Fi ETi+1Q

−1i Ei+1 +HT

i+1R−1i+1Hi+1

. (4.10)

Assim, Q+ATWA sera igual a

P−1i|i + F Ti Q

−1i Fi −F Ti Q

−1i Ei+1


−1i Ei+1 +HT

i+1R−1i+1Hi+1

(4.11)

e

ATWb =

−FTi 0

ETi+1 HTi+1

Q−1i 0

0 R−1i+1

Fixi|i

zi+1

=


ETi+1Q−1i Fixi|i +HT

i+1R−1i+1zi+1

. (4.12)

Substituindo-se o vetor

xi − xi|i

xi+1

, pelo vetor

xi|i+1 − xi|i

xi+1|i+1

, entao (4.9) pode ser

escrita como

xi|i+1 − xi|i

xi+1|i+1

=

P−1i|i + F Ti Q

−1i Fi −F Ti Q

−1i Ei+1


−1i Ei+1 +HT

i+1R−1i+1Hi+1

−1



i+1R−1i+1zi+1

. (4.13)

Entao


xi+1|i+1 =[

0 I]

P−1i|i + F Ti Q

−1i Fi −F Ti Q

−1i Ei+1


−1i Ei+1 +HT

i+1R−1i+1Hi+1

−1

×



i+1R−1i+1zi+1

. (4.14)

Usando-se o lema da inversao de blocos matriciais,

xi+1|i+1 =[−(D − CA−1B)−1CA−1 (D −CA−1B)−1

]

×



i+1R−1i+1zi+1

, (4.15)

ou

xi+1|i+1 = (D − CA−1B)−1(CA−1F Ti Q

−1i Fixi|i + ETi+1Q

−1i Fixi|i

+ HTi+1R

−1i+1zi+1

)(4.16)

sendo

(D − CA−1B)−1 =(ETi+1Q

−1i Ei+1 − E

Ti+1Q

−1i Fi(P

−1i|i + F Ti Q

−1i Fi)

−1F Ti Q−1i Ei+1

+ HTi+1R

−1i+1Hi+1

)−1

=(ETi+1(Q

−1i −Q

−1i Fi(P

−1i|i + F Ti Q

−1i Fi)

−1F Ti Q−1i )Ei+1

+ HTi+1R

−1i+1Hi+1

)−1

=(ETi+1(Qi + FiPi|iF

Ti )−1Ei+1 +HT

i+1R−1i+1Hi+1

)−1. (4.17)

Na forma matricial esta equacao pode ser escrita como

(D − CA−1B)−1 =

(

Ei+1

Hi+1

T

Qi + FiPi|iFTi 0

0 Ri+1

−1

Ei+1

Hi+1

)−1

. (4.18)

Definindo-se Pi+1|i+1 = (D − CA−1B)−1, entao


xi+1|i+1 = Pi+1|i+1

(−ETi+1Q

−1i Fi(P

−1i|i + F Ti Q

−1i Fi)

−1F Ti Q−1i Fixi|i +

+ ETi+1Q−1i Fixi|i +HT

i+1R−1i+1zi+1

)(4.19)

xi+1|i+1 = Pi+1|i+1ETi+1(Q

−1i −Q

−1i Fi(P

−1i|i + F Ti Q

−1i Fi)

−1F Ti Q−1i )Fixi|i

+ Pi+1|i+1HTi+1R

−1i+1zi+1 (4.20)

xi+1|i+1 = Pi+1|i+1

Ei+1

Hi+1

T

Qi + FiPi|iFTi 0

0 Ri+1

−1

Fixi|i

zi+1

. (4.21)

A solucao do Passo 0 e a mesma daquela encontrada pelo Teorema 2.1.1. �

4.2 Estimativa Robusta para Sistemas Singulares

Esta secao desenvolve o equacionamento do filtro considerando-se as incertezas de

modelagem. As incertezas estruturadas afetam as matrizes Ei+1, Fi e Hi+1 de (4.1),

que passa a ser re-escrita na seguinte forma

(Ei+1 + δEi+1)xi+1 = (Fi + δFi)xi + wi

yi+1 = (Hi+1 + δHi+1)xi+1 + vi+1. (4.22)

As incertezas nas matrizes Ei+1, Fi e Hi+1 sao modeladas como

δFi = Mf,i△1,iNf,i (4.23)

δEi+1 = Mf,i△1,iNe,i+1 (4.24)

δHi = Mh,i△2,iNh,i, (4.25)

sendo △1,i e △2,i matrizes arbitrarias satisfazendo ‖△1,i‖ ≤ 1 e ‖△2,i‖ ≤ 1. Com estas

informacoes sobre as incertezas, o funcional podera ser escrito como

minx0

maxδH0

[xT0 P−1i|i x0 + (z0 − (H0 + δH0)x0)

TR−10 (z0 − (H0 + δH0)x0)], (4.26)


para i = 0, e

min{xi,xi+1}

max{δEi+1,δFi,δHi+1}


i|i (xi − xi|i) + (zi+1

− (Hi+1 + δHi+1)xi+1)TR−1

i+1(zi+1 − (Hi+1 + δHi+1)xi+1) + ((Ei+1 + δEi+1)xi+1

− (Fi + δFi)xi)TQ−1

i ((Ei+1 + δEi+1)xi+1 − (Fi + δFi)xi)], (4.27)

para i > 0, sujeito as restricoes do modelo, Equacao (4.22), e as restricoes das incertezas,

equacoes (4.23), (4.24) e (4.25). Re-escrevendo-se o funcional (4.27) na forma matricial,

segue que

Ji =[

(xi − xi|i)T xTi+1

]

P−1i|i 0

0 0

xi − xi|i

xi+1

+

(

−(Fi + δFi) (Ei+1 + δEi+1)

0 (Hi+1 + δHi+1)

xi − xi|i

xi+1

−

(Fi + δFi)xi|i

zi+1

)T

Q−1i 0

0 R−1i+1

(.

)(4.28)

que escrito na forma compacta assume a seguinte expressao

Ji = minx

maxδA,δb

[xTQx+ [(A+ δA)x− (b+ δb)]TW (.)

], (4.29)

sendo

x ←

xi − xi|i

xi+1

;

b ←

Fixi|i

zi+1

;

A ←

−Fi Ei+1

0 Hi+1

;

δA ←

−δFi δEi+1

0 δHi+1

, ou

δA ←

Mf,i 0

0 Mh,i

△1,i 0

0 △2,i

−Nf,i Ne,i

0 Nh,i

;


δb ←

δFixi|i

0

, ou

δb ←

Mf,i 0

0 Mh,i

△1,i 0

0 △2,i

Nf,ixi|i

0

;

Q ←

P−1i|i 0

0 0

;

W ←

Q−1i 0

0 R−1i+1

;

H ←

Mf,i 0

0 Mh,i

;

Na ←

−Nf,i Ne,i

0 Nh,i

;

Nb ←

Nf,ixi|i

0

;

△ ←

△1,i 0

0 △2,i

.

No caso das condicoes iniciais, as equivalencias retiradas de (4.26) sao

A ← H0; b← z0;

δA ← δH0; δb← 0;

Q ← P−10 ; W ← R−1

0 ;

H ← Mh,0; Na ← Nh,0;

Nb ← 0.

Definindo-se Ei :=

Ei√λiNe,i

e Hi :=

Hi√λiNh,i

, entao a deducao da estimativa

filtrada robusta sera feita pelo teorema a seguir, seguindo o Teorema 3.1.1.

Teorema 4.2.1 Suponha que

Ei

Hi

tem posto coluna pleno para todo i ≥ 0. A

estimativa filtrada robusta otima xi|i de xi pode ser obtida a partir do seguinte algoritmo


recursivo

Passo 0: Condicoes Iniciais: Se Mh,0 = 0 entao

P0|0 :=(P−1

0 +HT0 R

−10 H0

)−1; (4.30)

x0|0 := P0|0HT0 R

−10 z0. (4.31)

Se Mh,0 6= 0 encontre o parametro escalar otimo λ−1 minimizando a funcao G(λ) do

Teorema 3.1.1 no intervalo λ >∥∥MT

h,0R−10 Mh,0

∥∥ e considere

R0 := R0 − λ−1−1Mh,0M

Th,0; (4.32)

P0|0 :=(P−1

0 +HT0 R

−10 H0 + λ−1N

Th,0Nh,0

)−1; (4.33)

x0|0 := P0|0HT0 R

−10 z0. (4.34)

Passo 1: Se Mf,i = 0 e Mh,i+1 = 0 entao λi := 0. Se nao, encontre o parametro escalar

otimo λi minimizando a funcao G(λ) do Teorema 3.1.1 no intervalo

λi > λl,i :=

∥∥∥∥∥

MTf,i 0

0 MTh,i+1

Q−1i 0

0 R−1i+1

Mf,i 0

0 Mh,i+1

∥∥∥∥∥. (4.35)

Passo 2: Se λi 6= 0, substitua os parametros {Qi, Ri+1, Pi|i, Ei+1, Fi,Hi+1} pelos

parametros corrigidos

Qi :=

Qi 0

0 I

sendo Qi := Qi − λ−1i Mf,iM

Tf,i; (4.36)

Ri+1 :=

Ri+1 0

0 I

, sendo Ri+1 := Ri+1 − λ−1i Mh,i+1M

Th,i+1; (4.37)

Ei+1 :=

Ei+1√λiNe,i+1

(4.38)

Fi :=

Fi√λiNf,i

(4.39)

Hi+1 :=

Hi+1√λiNh,i+1

. (4.40)


Passo 3: Atualize {Pi|i, xi|i} para {Pi+1|i+1, xi+1|i+1} do seguinte modo

Pi+1|i+1 :=

(

Ei+1

Hi+1

T

Qi + FiPi|iFTi 0

0 Ri+1

−1

Ei+1

Hi+1

)−1

, (4.41)

xi+1|i+1 = Pi+1|i+1

Ei+1

Hi+1

T

Qi + FiPi|iFTi 0

0 Ri+1

−1

Fixi|i

Zi+1

, (4.42)

sendo

Zi+1 :=

zi+1

0

. (4.43)

Prova: De acordo com SAYED (2001), a solucao de (4.29) e dada por

x = [Q+AT WA]−1[AT Wb+ λiNTa Nb] (4.44)

sendo Q := Q + λiNTa Na e W := W + WH(λiI − HTWH)†HTW . Pelo lema da

inversao de matrizes a expressao de W pode ser escrita como W−1 = W−1−λ−1i HHT =

W−1 − λ−1i MiM

Ti . Sendo assim, entao

Q = Q+ λiNTa Na

=

P−1i|i 0

0 0

+ λi

−NTf,i 0

NTe,i NT

h,i

−Nf,i Ne,i

0 Nh,i

=

(P−1i|i + λiN

Tf,iNf,i) −λiN

Tf,iNe,i

−λiNTe,iNf,i λi(N

Te,iNe,i +NT

h,iNh,i)

(4.45)

e a equacao W = (W−1 − λ−1i MiM

Ti )−1 e dada por

W = (

Qi 0

0 Ri+1

− λ−1i

Mf,iMTf,i 0

0 Mh,iMTh,i

)−1, (4.46)

ou


W =

(Qi − λ−1i Mf,iM

Tf,i) 0

0 (Ri+1 − λ−1i Mh,iM

Th,i)

−1

,

=

Q−1i 0

0 R−1i+1

. (4.47)

O termo AT WA e expresso como

AT WA =

−FTi 0

ETi+1 HTi+1

Q−1i 0

0 R−1i+1

−Fi Ei+1

0 Hi+1

=


−1i Ei+1


−1i Ei+1 +HT

i+1R−1i+1Hi+1

(4.48)

O termo AT Wb e expresso como

AT Wb =

−FTi 0

ETi+1 HTi+1

Q−1i 0

0 R−1i+1

Fixi|i

zi+1

=



i+1R−1i+1zi+1

. (4.49)

Assim

(

(P−1i|i + λiN

Tf,iNf,i) −λiN

Tf,iNe,i

−λiNTe,iNf,i λi(N

Te,iNe,i +NT

h,iNh,i)

+


−1i Ei+1


−1i Ei+1 +HT

i+1R−1i+1Hi+1

)

(xi|i+1 − xi|i)

xi+1|i+1

=

(



i+1R−1i+1zi+1

+ λi

−NTf,iNf,ixi|i

NTe,iNf,ixi|i

)

(4.50)

xi|i+1 − xi|i

xi+1|i+1

=

F Ti Q−1i Fi + P−1

i|i −F Ti Q−1i Ei+1


−1i Ei+1 + HT

i+1R−1i+1Hi+1

−1

×


ETi+1Q−1i Fixi|i + HT

i+1R−1i+1Zi+1

(4.51)


e

xi+1|i+1 =[

0 I]

F Ti Q−1i Fi + P−1

i|i −F Ti Q−1i Ei+1


−1i Ei+1 + HT

i+1R−1i+1Hi+1

−1

×



i+1R−1i+1Zi+1

. (4.52)

Usando-se o lema da inversao de blocos matriciais, obtem-se

xi+1|i+1 =[−(D − CA−1B)−1CA−1 (D −CA−1B)−1

]

×



i+1R−1i+1Zi+1

. (4.53)

Assim

xi+1|i+1 = (D − CA−1B)−1

(CA−1F Ti Q


−1i Fixi|i

+ HTi+1R

−1i+1Zi+1

). (4.54)

e

(D − CA−1B)−1 =

(ETi+1Q

−1i Ei+1 + HT

i+1R−1i+1Hi+1 − E

Ti+1Q

−1i Fi(F

Ti Q

−1i Fi

+ P−1i|i )−1F Ti Q

−1i Ei+1

)−1

=

(ETi+1(Q

−1i − Q

−1i Fi(F

Ti Q

−1i Fi

+ P−1i|i )−1F Ti Q

−1i )Ei+1 + HT

i+1R−1i+1Hi+1

)−1

. (4.55)

Usando-se o lema da inversao de matrizes nesta equacao, encontra-se

(D − CA−1B)−1 =

(ETi+1(Qi + FiPi|iF

Ti )−1Ei+1 + HT

i+1R−1i+1Hi+1

)−1

.(4.56)

Definindo-se Pi+1|i+1 := (D−CA−1B)−1, e pondo-se esta equacao na forma matricial,

entao

Pi+1|i+1 =

(

Ei+1

Hi+1

T

Qi + FiPi|iFTi 0

0 Ri+1

−1

Ei+1

Hi+1

)−1

. (4.57)


Ei+1 =

I

0

, Hi+1 =

Hi+1

0

, Ri+1 =

Ri+1 0

0 I

, Qi =

Qi 0

0 I

.

Assim a expressao

Pi+1|i+1 :=

(ETi+1(Qi + FiPi|iF

Ti )−1Ei+1 + HT

i+1R−1i+1Hi+1

)−1

(4.63)

fica sendo

Pi+1|i+1 =

(

I

0

T(

Qi 0

0 I

+

Fi√λiNf,i

Pi|i

Fi√λiNf,i

T)−1

I

0

+

Hi+1

0

T

Ri+1 0

0 I

−1

Hi+1

0

)−1

(4.64)

ou

Pi+1|i+1 =

(

I

0

T(

Qi + FiPi|iFTi

√λiFiPi|iN

Tf,i√

λiNf,iPi|iFTi I + λiNf,iPi|iN

Tf,i

)−1

I

0

+ HTi+1R

−1i+1Hi+1

)−1

. (4.65)

Aplicando-se o lema da inversao de blocos matriciais a Equacao (4.65), obtem-se

Pi+1|i+1 =

((Qi + Fi(P

−1i|i + λiN

Tf,iNf,i)

−1F Ti

)−1+HT

i+1R−1i+1Hi+1

)−1

.(4.66)

Como Pi|i = (P−1i|i + λiN

Tf,iNf,i)

−1, entao

Pi+1|i+1 =

((Qi + FiPi|iF

Ti )−1 +HT

i+1R−1i+1Hi+1

)−1

. (4.67)

Quanto a expressao do filtro tem-se

xi+1|i+1 = Pi+1|i+1

I

0

T (

Qi 0

0 I

+

Fi√λiNf,i

Pi|i

Fi√λiNf,i

T)−1

×

Fi√λiNf,i

xi|i + Pi+1|i+1

Hi+1

0

T

Ri+1 0

0 I

−1

zi+1

0

(4.68)


e aplicando-se o lema da inversao de matrizes ao primeiro termo do segundo membro

desta equacao, tem-se

xi+1|i+1 =

((Qi + FiPi|iF

Ti )− (Qi + FiPi|iF

Ti )HT

i+1(Ri+1 +Hi+1(Qi + FiPi|iFTi )

× HTi+1)

−1Hi+1(Qi + FiPi|iFTi )

)(Qi + FiPi|iF

Ti )−1Fc,ixi|i

+ Pi+1|i+1HTi+1R

−1i+1zi+1 ou (4.76)

xi+1|i+1 = Fc,ixi|i − (Qi + FiPi|iFTi )HT

i+1

(Ri+1 +Hi+1(Qi + FiPi|iF

Ti )HT

i+1

)−1

× Hi+1Fc,ixi|i + Pi+1|i+1HTi+1R

−1i+1zi+1, (4.77)

que tambem pode ser expressa como

xi+1|i+1 = Fc,ixi|i −((Qi + FiPi|iF

Ti )−1 +HT

i+1R−1i+1Hi+1

)−1HTi+1R

−1i+1Hi+1Fc,ixi|i

+ Pi+1|i+1HTi+1R

−1i+1zi+1, ou (4.78)

xi+1|i+1 = Fc,ixi|i − Pi+1|i+1HTi+1R

−1i+1Hi+1Fc,ixi|i + Pi+1|i+1H

Ti+1R

−1i+1zi+1. (4.79)

Sendo que em funcao do erro de estimativa, a versao no espaco de estados e expressa

da seguinte maneira

xi+1|i+1 = Fc,ixi|i + Pi+1|i+1HTi+1R

−1i+1(zi+1 −Hi+1Fc,ixi|i). (4.80)

Pode-se entao comparar o algoritmo apresentado neste capıtulo com o apresentado

em SAYED (2001) para o espaco de estados usual, quando (Ei+1 = I), e quando as

incertezas estao presentes somente na matriz Fi. Destacam-se as expressoes (4.67) e

(4.74),


Ti )−1 +HT

i+1R−1i+1Hi+1

)−1; (4.81)


Ti+1R

−1i+1zi+1 (4.82)

sendo Qi = Qi − λ−1i Mf,iM

Tf,i. As equacoes correspondentes de SAYED (2001) sao

dadas por



Ti )−1 +HT

i+1R−1i+1Hi+1

)−1; (4.83)


Ti+1R

−1i+1zi+1 (4.84)

sendo Ri+1 = Ri+1 − λ−1i Hi+1Mf,iM

Tf,iH

Ti+1. As expressoes para Pi|i e Fc,i sao as

mesmas para ambos os filtros, mas o intervalo de ajuste para o parametro de otimizacao

λ e diferente. Observe que o filtro proposto nesta tese, apesar de ser diferente do

filtro proposto em SAYED (2001), mantem a propriedade de regularizacao ou seja, os

intervalos de ajuste de λ sao conhecidos a-priori pois dependem somente dos parametros

do sistema. Os funcionais de ambos os filtros sao diferentes, mas ambos se reduzem ao

filtro de Kalman usual quando o sistema nao esta sujeito a incertezas.

4.4 Estimativa Suavizadora Robusta

A estimativa suavizadora robusta singular pode ser encontrada com facilidade a

partir da Equacao (4.51) do Teorema 4.2.1. Explicitando-se o termo xi|i+1 naquela

equacao e apos algumas manipulacoes algebricas, encontra-se que a estimativa sua-

vizadora robusta e dada por

xi|i+1

= xi|i − Pi|iFTi (Qi + FiPi|iF

Ti )−1

(I − Ei+1Pi+1|i+1E

Ti+1(Qi + FiPi|iF

Ti )−1

)Fixi|i

+ Pi|iFTi (Qi + FiPi|iF

Ti )−1Ei+1Pi+1|i+1H

Ti+1R

−1i+1Zi+1. (4.85)

4.5 Exemplo Numerico

Exemplo 4.5.1 Considere o sistema singular com incertezas estruturadas modeladas

de acordo com as equacoes (4.22) - (4.25), cujas matrizes sao dadas por


E =

1 0 0

0 1 0

0 0 0

, F =

0.9 0 0

0 0.8 0

0.2 0.2 0.2

, H =

[1.4 0.8 1

],

Q =

1.2 0 0

0 1.6 0

0 0 2

, Nf =

0.05 0 0

0 0.05 0

0 0 0.13

, Ne =

0.1 0 0

0 0.1 0

0 0 0

,

Nh =

2 0 0

0 28.18 0

0 0 2

,Mf =

0.5 0 0

0 0.5 0

0 0 1.3

,

R = 0.16, Mh =[

0.8 0.8 0.8].

(4.86)

Os resultados da Figura 4.1 foram simulados considerando-se as matrizes (4.86), para

todo i > 0 e o sistema sem incerteza, para i = 0. A Figura 4.1 mostra as curvas das

variancias dos erros calculadas via Monte-Carlo cuja expressao e dada por

E‖xi − xi‖ ≈1

T

T∑

j=1

‖x(j)i − x

(j)i ‖. (4.87)

Cada ponto no instante i em cada curva da variancia e a media calculada sobre T = 800

experimentos. Para cada experimento j, a matriz ∆ com norma menor ou igual a um

e selecionada aleatoriamente e fixada para todo i. Gera-se T = 800 trajetorias de 1000

pontos cada. Os filtros considerados sao: o de Maxima Verossimilhanca (ML) que e

apresentado em NIKOUKHAH et al. (1992), com uma abordagem estocastica mas

que se assemelha as expressoes apresentadas no Teorema 4.1.1, implementado com os

parametros nominais e aplicado ao sistema com incertezas; o otimo do Teorema 4.1.1

implementado com os parametros nominais e aplicado ao sistema sem incertezas e o

Descriptor Robusto (DR), Teorema 4.2.1. O filtro DR apresenta melhor desempenho

que o filtro ML (o parametro λi e fixado em λ = 80λl, para todo i).


100

101

102

103

5

10

15

20

25

30

i

Var

ian

cia

do

Err

o (

dB

)

ML

DR

Ótimo

Figura 4.1: Filtros Descriptor Robusto (DR), Otimo, e de Maxima Verossimilhanca(ML).

Capıtulo 5

Estimativa Preditora para

Sistemas Singulares

Este capıtulo apresenta inicialmente algoritmos de filtragem para a estimativa predi-

tora e a estimativa preditora-corretora sem robustez para o sistema singular (4.1), em

seguida apresenta um algoritmo para a estimativa preditora robusta singular e compara

a estimativa preditora singular sem robustez com a estimativa preditora no espaco de

estados. Finalmente encontra a expressao da estimativa preditora-corretora robusta

singular.

5.1 Estimativa Preditora Singular

O estudo da estimativa preditora recursiva para o sistema singular consiste em se

achar uma sequencia {x0|i, x1|i, x2|i, . . . xi+1|i} a partir de uma sequencia de medidas

{z0, z1, z2, . . . zi}. Ao inves de se fazer uma abordagem estocastica, este trabalho adota

a abordagem determinıstica usando-se o metodo dos mınimos quadrados recursivos

atraves da minimizacao do seguinte funcional

Ji = minxi,xi+1

[(xi − xi|i−1)TP−1

i|i−1(xi − xi|i−1) + (zi −Hixi)TR−1

i (zi −Hixi)

+ (Ei+1xi+1 − Fixi)TQ−1

i (Ei+1xi+1 − Fixi)]. (5.1)

A solucao deste sistema e dada pelo seguinte teorema:

60

CAPITULO 5. ESTIMATIVA PREDITORA PARA SISTEMAS SINGULARES 61

Teorema 5.1.1 Suponha que a matriz Ei+1 tem posto coluna pleno para todo i ≥ 0 e e

dada uma sequencia de medidas {z0, z1, z2, . . . zi}. A estimativa preditora otima xi+1|i

resultante da minimizacao do funcional Ji (5.1), pode ser obtida a partir do seguinte

algoritmo recursivo.

Passo 0: Condicoes Iniciais

P0|−1 = P0 (5.2)

x0|−1 = 0. (5.3)

Passo i: Atualize os termos {xi|i−1, Pi|i−1} para {xi+1|i, Pi+1|i} atraves das recursoes

xi+1|i = Pi+1|i

Ei+1

0

T

Qi + FiPi|i−1FTi −FiPi|i−1H

Ti

−HiPi|i−1FTi (Ri +HiPi|i−1H

Ti )

−1

Fixi|i−1

zi −Hixi|i−1

,

(5.4)

sendo

Pi+1|i =

(

Ei+1

0

T


Ti

−HiPi|i−1FTi Ri +HiPi|i−1H

Ti

−1

Ei+1

0

)−1

.

(5.5)

Prova: Re-escrevendo-se o funcional Ji (5.1) na forma matricial, obtem-se

[(xi − xi|i−1)

T xTi+1

]

P−1i|i−1 0

0 0

xi − xi|i−1

xi+1

+

(

−Fi Ei+1

Hi 0

xi − xi|i−1

xi+1

−

Fixi|i−1

zi −Hixi|i−1

)T

Q−1i 0

0 R−1i

(.

).

(5.6)

Comparando-se os termos desta equacao com a equacao dos mınimos quadrados regu-

larizados de (SAYED (2001)), obtem-se as seguintes equivalencias


x ←

xi − xi|i−1

xi+1

b ←

Fixi|i−1

zi −Hixi|i−1

Q ←

P−1i|i−1 0

0 0

A ←

−Fi Ei+1

Hi 0

W ←

Q−1i 0

0 R−1i

,

cuja solucao e

x = [Q+ATWA]−1ATWb. (5.7)

O termo ATWA fica sendo

ATWA =

−FTi HT

i

ETi+1 0

Q−1i 0

0 R−1i

−Fi Ei+1

Hi 0

=

F Ti Q−1i Fi +HT

i R−1i Hi −F

Ti Q

−1i Ei+1


−1i Ei+1

. (5.8)

Assim, Q+ATWA sera igual a

P−1i|i−1

+ F Ti Q−1i Fi +HT

i R−1i Hi −F

Ti Q

−1i Ei+1


−1i Ei+1

, (5.9)

e o termo

ATWb =

−FTi HT

i

ETi+1 0

Q−1i 0

0 R−1i

Fixi|i−1

zi −Hixi|i−1


que resulta em

ATWb =

(HTi R

−1i zi − (F Ti Q

−1i Fi +HT

i R−1i Hi)xi|i−1)

ETi+1Q−1i Fixi|i−1

. (5.10)

Substituindo-se o vetor

(xi − xi|i−1)

xi+1

pelo vetor

(xi|i − xi|i−1)

xi+1|i

, entao a Equa-

cao (5.7) pode ser escrita como

(xi|i − xi|i−1)

xi+1|i

=


−1i Fi +HT

i R−1i Hi −F

Ti Q

−1i Ei+1


−1i Ei+1

−1

×

(HTi R


−1i Fi +HT



. (5.11)

Entao

xi+1|i =[

0 I]


−1i Fi +HT

i R−1i Hi −F

Ti Q

−1i Ei+1


−1i Ei+1

−1

×

(HTi R


−1i Fi +HT



. (5.12)

Usando-se o lema da inversao de blocos matriciais, entao esta equacao pode ser escrita

como

xi+1|i =[−(D − CA−1B)−1CA−1 (D − CA−1B)−1

]

×

(HTi R


−1i Fi +HT



. (5.13)

Entao

xi+1|i = (D − CA−1B)−1ETi+1Q−1i Fi(P

−1i|i−1 + F Ti Q

−1i Fi +HT

i R−1i Hi)

−1

× (HTi R


−1i Fi +HT


+ (D − CA−1B)−1ETi+1Q−1i Fixi|i−1, (5.14)

sendo


5.1.1 Estimativa Preditora - Corretora Singular

A estimativa preditora-corretora singular associa a expressao da estimativa filtrada

com a expressao da estimativa preditora e pode ser obtida a partir do Lema a seguir.

Lema 5.1.1 A atualizacao no tempo para a estimativa preditora-corretora de sistemas

singulares e dada pela seguinte expressao

xi+1|i =(ETi+1Q

−1i Ei+1

)−1ETi+1Q

−1i Fixi|i. (5.25)

Prova: Explicitando-se o termo xi|i da Equacao (5.11) do Teorema 5.1.1, obtem-se

xi|i = xi|i−1 +[I 0

]


−1i Fi +HT

i R−1i Hi −F

Ti Q

−1i Ei+1


−1i Ei+1

−1

×

(HTi R


−1i Fi +HT



. (5.26)

Aplicando-se o lema da inversao de blocos matriciais nesta matriz inversa, obtem-se

xi|i = xi|i−1 +[A−1 +A−1B(D −CA−1B)−1CA−1 −A−1B(D − CA−1B)−1

]

×

(HTi R


−1i Fi +HT



, ou (5.27)

xi|i = xi|i−1 +A−1(HTi R


−1i Fi +HT


+ A−1B(D − CA−1B)−1CA−1(HTi R


−1i Fi +HT


− A−1B(D − CA−1B)−1ETi+1Q−1i Fixi|i−1 (5.28)

xi|i = xi|i−1 +A−1HTi R

−1i zi −A

−1(F Ti Q−1i Fi +HT

i R−1i Hi)xi|i−1

+ A−1B(D − CA−1B)−1CA−1HTi R

−1i zi −A

−1B(D − CA−1B)−1CA−1

× (F Ti Q−1i Fi +HT

i R−1i Hi)xi|i−1 −A

−1B(D − CA−1B)−1

× ETi+1Q−1i Fixi|i−1 (5.29)


xi|i =(I −A−1(F Ti Q

−1i Fi +HT

i R−1i Hi)−A

−1B(D − CA−1B)−1CA−1

× (F Ti Q−1i Fi +HT

i R−1i Hi)−A

−1B(D − CA−1B)−1ETi+1Q−1i Fi

)xi|i−1

+ A−1(I +B(D − CA−1B)−1CA−1

)HTi R

−1i zi (5.30)

xi|i = A−1(A− (F Ti Q

−1i Fi +HT

i R−1i Hi)−B(D − CA−1B)−1CA−1(F Ti Q

−1i Fi

+ HTi R

−1i Hi)−B(D − CA−1B)−1ETi+1Q

−1i Fi

)xi|i−1

+ A−1(I +B(D − CA−1B)−1CA−1

)HTi R

−1i zi (5.31)

xi|i = A−1(P−1i|i−1 − F

Ti Q

−1i Ei+1(D − CA

−1B)−1ETi+1Q−1i FiA

−1(F Ti Q−1i Fi

+ HTi R

−1i Hi) + F Ti Q

−1i Ei+1(D − CA

−1B)−1ETi+1Q−1i Fi

)xi|i−1

+ A−1(I + F Ti Q

−1i Ei+1(D −CA


−1)HTi R

−1i zi (5.32)

xi|i = A−1

(P−1i|i−1 + F Ti Q

−1i Ei+1(D − CA


(I −A−1(F Ti Q

−1i Fi

+ HTi R

−1i Hi

))xi|i−1

+ A−1(I + F Ti Q

−1i Ei+1(D − CA


−1)HTi R

−1i zi, (5.33)

xi|i = A−1

(I + F Ti Q

−1i Ei+1(D − CA


−1

)P−1i|i−1xi|i−1

+ A−1(I + F Ti Q

−1i Ei+1(D − CA


−1)HTi R

−1i zi. (5.34)

Assim

xi|i−1 = Pi|i−1

(A−1 +A−1F Ti Q

−1i Ei+1(D − CA


−1

)−1

xi|i

− Pi|i−1HTi R

−1i zi. (5.35)

A expressao do preditor encontrada na Equacao (5.14) e definida como

xi+1|i = (D − CA−1B)−1

(ETi+1Q

−1i Fi(P

−1i|i−1 + F Ti Q

−1i Fi +HT

i R−1i Hi)

−1

× (HTi R


−1i Fi +HT

i R−1i Hi)xi|i−1) + ETi+1Q

−1i Fixi|i−1

),

(5.36)


ou


−1i|i−1 + F Ti Q

−1i Fi +HT

i R−1i Hi)

−1

× HTi R

−1i zi − (D − CA−1B)−1ETi+1Q

−1i Fi(P

−1i|i−1 + F Ti Q

−1i Fi

+ HTi R

−1i Hi)


i R−1i Hi)xi|i−1

+ (D − CA−1B)−1ETi+1Q−1i Fixi|i−1 (5.37)

xi+1|i = (D − CA−1B)−1ETi+1Q−1i Fi

(I − (P−1

i|i−1 + F Ti Q−1i Fi

+ HTi R

−1i Hi)


i R−1i Hi

)xi|i−1 + (D − CA−1B)−1

× ETi+1Q−1i Fi(P

−1i|i−1 + F Ti Q

−1i Fi +HT

i R−1i Hi)

−1HTi R

−1i zi (5.38)


−1i|i−1


i R−1i Hi)

−1P−1i|i−1

xi|i−1

+ (D − CA−1B)−1ETi+1Q−1i Fi(P

−1i|i−1 + F Ti Q

−1i Fi +HT

i R−1i Hi)

−1HTi R

−1i zi.

(5.39)

Substituindo-se nesta equacao o valor de xi|i−1 da Equacao (5.35), obtem-se


−1i|i−1 + F Ti Q

−1i Fi

+ HTi R

−1i Hi)

−1P−1i|i−1

(Pi|i−1

(A−1 +A−1F Ti Q

−1i Ei+1(D

− CA−1B)−1ETi+1Q−1i FiA

−1)−1

xi|i − Pi|i−1HTi R

−1i zi

)


−1i|i−1 + F Ti Q

−1i Fi +HT

i R−1i Hi)

−1HTi R

−1i zi


−1i|i−1 + F Ti Q

−1i Fi +HT

i R−1i Hi)

−1

×(A−1 +A−1F Ti Q

−1i Ei+1(D − CA


−1)−1

xi|i

− (D − CA−1B)−1ETi+1Q−1i Fi(P

−1i|i−1 + F Ti Q

−1i Fi +HT

i R−1i Hi)

−1HTi R

−1i zi


−1i|i−1 + F Ti Q

−1i Fi +HT

i R−1i Hi)

−1HTi R

−1i zi,


xi+1|i = (D − CA−1B)−1ETi+1Q−1i FiA

−1

×(A−1 +A−1F Ti Q

−1i Ei+1(D − CA


−1)−1

xi|i

= (D − CA−1B)−1ETi+1Q−1i Fi

(I +A−1F Ti Q

−1i Ei+1(D − CA

−1B)−1

× ETi+1Q−1i Fi

)−1xi|i

=(D − CA−1B + ETi+1Q

−1i FiA


)−1ETi+1Q

−1i Fixi|i. (5.40)

Entao

xi+1|i =(ETi+1Q

−1i Ei+1 − E

Ti+1Q

−1i FiA


+ ETi+1Q−1i FiA


)−1ETi+1Q

−1i Fixi|i (5.41)

xi+1|i =(ETi+1Q

−1i Ei+1

)−1ETi+1Q

−1i Fixi|i. (5.42)

�

Nota: De (5.42) tem-se que

ETi+1Q−1i

(Ei+1xi+1|i − Fixi|i

)= 0. (5.43)

Como no Teorema 5.1.1 foi considerado Ei+1 posto coluna pleno para a existencia

do filtro preditor, de (5.43) pode-se concluir que

Ei+1xi+1|i = Fixi|i (5.44)

somente se for considerado Ei+1 tambem com posto linha pleno, ou seja, se Ei+1 for

invertıvel. Segue tambem que se Ei+1 = I entao obtem-se a expressao usual para a

atualizacao da estimativa no tempo

xi+1|i = Fixi|i.


5.2 Estimativa Preditora Robusta Singular

Considere o sistema

(Ei+1 + δEi+1)xi+1 = (Fi + δFi)xi + wi (5.45)

yi = (Hi + δHi)xi + vi (5.46)

sendo as incertezas nas matrizes Ei+1, Fi e Hi modeladas como

δFi δEi+1

δHi 0

=

Mf,i 0

0 Mh,i

△1,i 0

0 △2,i

Nf,i Ne,i+1

Nh,i 0

. (5.47)

Considere o problema de otimizacao

min{xi,xi+1}

max{δEi+1,δFi,δHi}

[(xi − xi|i−1)

TP−1i|i−1(xi − xi|i−1) +

(zi − (Hi + δHi)xi

)T

× R−1i


)+

((Ei+1 + δEi+1)xi+1 − (Fi + δFi)xi

)T

× Q−1i


)], (5.48)

sujeito as restricoes (5.45) e (5.46) e as incertezas representadas por (5.47). Definindo-

se Ei+1 :=

Ei+1√λiNe,i+1

e seguindo-se a mesma sequencia de calculo adotada para a

estimativa preditora singular sem incertezas, pode-se enunciar o seguinte Teorema

Teorema 5.2.1 Suponha que a matriz Ei+1 tem posto coluna pleno para todo i ≥ 0 e

e dada a sequencia de medidas {z0, z1, z2, . . . zi}. A estimativa preditora otima xi+1|i

resultante da solucao do problema min-max do funcional Ji sujeito a restricao (5.46)

e as incertezas representadas por (5.47) pode ser obtida a partir do seguinte algoritmo

recursivo.

Passo 0: Condicoes Iniciais

P0|−1 = P0 (5.49)

x0|−1 = 0, (5.50)

Passo 1: Se Mf,i = 0 e Mh,i = 0 entao λi := 0. Se nao, encontre o parametro escalar


otimo λi minimizando a funcao G(λ) do Teorema 3.1.1, no intervalo

λi > λl,i :=

∥∥∥∥∥

MTf,i 0

0 MTh,i

Q−1i 0

0 R−1i

Mf,i 0

0 Mh,i

∥∥∥∥∥. (5.51)

Passo 2: Se λi 6= 0, substitua os parametros {Qi, Ri, Pi|i−1, Ei+1, Fi,Hi} pelos parame-

tros corrigidos

Qi :=

Qi 0

0 I

sendo Qi := Qi − λ−1i Mf,iM

Tf,i; (5.52)

Ri :=

Ri 0

0 I

, sendo Ri := Ri − λ−1i Mh,iM

Th,i; (5.53)

Ei+1 :=

Ei+1√λiNe,i+1

; (5.54)

Fi :=

Fi√λiNf,i

; (5.55)

Hi :=

Hi√λiNh,i

. (5.56)

Passo 3: Atualize {Pi|i−1, xi|i−1} para {Pi+1|i, xi+1|i} do seguinte modo

Pi+1|i =

(

Ei+1

0

T


Ti

−HiPi|i−1FTi Ri + HiPi|i−1H

Ti

−1

Ei+1

0

)−1

,

(5.57)

xi+1|i = Pi+1|i

Ei+1

0

T


Ti


Ti

−1

Fixi|i−1

Zi

,

(5.58)

sendo

Zi :=

zi

0

. (5.59)


Prova: O funcional Ji do problema de otimizacao (5.48) pode ser escrito na seguinte

forma

Ji =

xi|i−1 − xi

xi+1

T

P−1i|i−1 0

0 0

xi|i−1 − xi

xi+1

+

((

Fi Ei+1

Hi 0

+

δFi δEi+1

δHi 0

)

xi|i−1 − xi

xi+1

−(

Fixi|i−1

Hixi|i−1 − zi

+

δFixi|i−1

δHixi|i−1

))T

Q−1i 0

0 R−1i

(.

),

(5.60)

que de maneira compacta pode ser re-escrito como

J = xTQx+

((A+ δA)x − (b+ δb)

)TW

((A+ δA)x − (b+ δb)

). (5.61)

Comparando-se os termos desta equacao com a equacao dos mınimos quadrados regu-

larizados de (SAYED (2001)), obtem-se as seguintes equivalencias

x←

xi|i−1 − xi

xi+1

; A←

Fi Ei+1

Hi 0

; b←

Fixi|i−1

Hixi|i−1 − zi

;

δA←

δFi δEi+1

δHi 0

=

Mf,i 0

0 Mh,i

△1,i 0

0 △2,i

Nf,i Ne,i+1

Nh,i 0

δb←

δFixi|i−1

δHixi|i−1

=

Mf,i 0

0 Mh,i

△1,i 0

0 △2,i

Nf,ixi|i−1

Nh,ixi|i−1

Q←

P−1i|i−1 0

0 0

; W ←

Q−1i 0

0 R−1i

; H ←

Mf,i 0

0 Mh,i

;

Na ←

Nf,i Ne,i+1

Nh,i 0

; Nb ←

Nf,ixi|i−1

Nh,ixi|i−1

; △←

△1,i 0

0 △2,i


cuja solucao e

x =(Q+AT WA

)−1 (AT W b+ λiN

Ta Nb

), sendo (5.62)

Q = Q+ λiNTa Na

=

P−1i|i−1 0

0 0

+ λi

NTf,i NT

h,i

NTe,i+1 0

Nf,i Ne,i+1

Nh,i 0

=

P−1i|i−1 + λiN

Tf,iNf,i + λiN

Th,iNh,i λiN

Tf,iNe,i+1

λiNTe,i+1Nf,i λiN

Te,i+1Ne,i+1

(5.63)

e

W =

(

Qi 0

0 Ri

− λ−1i

Mf,iMTf,i 0

0 Mh,iMTh,i

)−1

=

Qi − λ−1i Mf,iM

Tf,i 0

0 Ri − λ−1i Mh,iM

Th,i

−1

. (5.64)

Usando-se as variaveis auxiliares Qi e Ri, pode-se escrever os termos AT WA e AT Wb

como

AT WA =

F Ti HTi

ETi+1 0

Qi 0

0 Ri

−1

Fi Ei+1

Hi 0

=

F Ti Q−1i Fi +HT

i R−1i Hi F Ti Q

−1i Ei+1

ETi+1Q−1i Fi ETi+1Q

−1i Ei+1

(5.65)

AT W b =

F Ti HTi

ETi+1 0

Q−1i 0

0 R−1i

Fixi|i−1

Hixi|i−1 − zi

=




. (5.66)

Substituindo-se os valores encontrados em (5.64),(5.65) e (5.66) em (5.62) e conside-

rando-se que agora


x =

xi|i−1 − xi|i

xi+1|i

,

obtem-se

xi|i−1 − xi|i

xi+1|i

=

(

P−1i|i−1 + λiN

Tf,iNf,i + λiN

Th,iNh,i λiN

Tf,iNe,i+1

λiNTe,i+1Nf,i λiN

Te,i+1Ne,i+1

+

F Ti Q−1i Fi +HT

i R−1i Hi F Ti Q

−1i Ei+1


−1i Ei+1

)−1

×

(




+ λi

(NTf,iNf,i +NT

h,iNh,i

)xi|i−1

NTe,i+1Nf,ixi|i−1

)

,

(5.67)

ou de maneira compacta

xi|i−1 − xi|i

xi+1|i

=

(FTi Q−1i Fi + H

Ti R

−1i Hi + P−1

i|i−1) FTi Q−1i Ei+1


−1i Ei+1

−1

×

(FTi Q−1i Fi + H

Ti R

−1i Hi)xi|i−1 − H

Ti R

−1i Zi


. (5.68)

Explicitando-se o termo xi+1|i, resulta

xi+1|i =[

0 I]

(FTi Q−1i Fi + H

Ti R

−1i Hi + P−1

i|i−1) FTi Q−1i Ei+1


−1i Ei+1

−1

×

(FTi Q−1i Fi + H

Ti R


Ti R

−1i Zi


. (5.69)

Aplicando-se o lema da inversao de blocos matriciais a Equacao (5.69), obtem-se


xi+1|i =[−(D − CA−1B)−1CA−1 (D − CA−1B)−1

]

×

(FTi Q−1i Fi + H

Ti R


Ti R

−1i Zi


. (5.70)

Entao

xi+1|i = (D − CA−1B)−1(−CA−1(FTi Q

−1i Fi + H

Ti R

−1i Hi) + ETi+1Q

−1i Fi

)xi|i−1

+ (D − CA−1B)−1CA−1HTi R−1i Zi, (5.71)

sendo

(D − CA−1B)−1 =

=

(ET

i+1Q−1

i Ei+1 − ETi+1Q

−1

i Fi(FTi Q

−1

i Fi + HTi R

−1

i Hi + P−1

i|i−1)−1FT

i Q−1

i Ei+1

)−1

=

(ET

i+1

(Qi + FiPi|i−1F

Ti − FiPi|i−1H

Ti (Ri + HiPi|i−1H

Ti )−1HiPi|i−1F

Ti

)−1

Ei+1

)−1

.

(5.72)

Considerando-se Pi+1|i := (D − CA−1B)−1, entao

Pi+1|i :=

(ETi+1

(Qi + FiPi|i−1F

Ti − FiPi|i−1H


Ti )−1HiPi|i−1F

Ti

)−1Ei+1

)−1

(5.73)

ou na forma de blocos matriciais

Pi+1|i :=

(

Ei+1

0

T


Ti


Ti

−1

Ei+1

0

)−1

.

(5.74)

Assim, a Equacao (5.71) assume a seguinte forma

xi+1|i = Pi+1|i

(−CA−1(FTi Q

−1i Fi + H

Ti R

−1i Hi) + ETi+1Q

−1i Fi

)xi|i−1

+ Pi+1|iCA−1HTi R

−1i Zi, (5.75)


xi+1|i = Pi+1|i

(−ETi+1Q

−1i Fi(F

Ti Q

−1i Fi + H

Ti R

−1i Hi + P−1

i|i−1)−1FTi Q

−1i Fi

− ETi+1Q−1i Fi(F

Ti Q

−1i Fi + H

Ti R

−1i Hi + P−1

i|i−1)−1HTi R

−1i Hi

+ ETi+1Q−1i Fi

)xi|i−1 + Pi+1|iE

Ti+1Q

−1i Fi(F

Ti Q

−1i Fi + H

Ti R

−1i Hi

+ P−1i|i−1)

−1HTi R−1i Zi, (5.76)


(Q−1i − Q

−1i Fi(F

Ti Q

−1i Fi + H

Ti R

−1i Hi + P−1

i|i−1)−1FTi Q

−1i

)

× Fixi|i−1 + Pi+1|iETi+1Q

−1i Fi(F

Ti Q

−1i Fi + H

Ti R

−1i Hi + P−1

i|i−1)−1HTi R

−1i

×(Zi − Hixi|i−1

). (5.77)

Aplicando-se o lema da inversao de matrizes a esta equacao, obtem-se


((Qi + FiPi|i−1F

Ti )− FiPi|i−1H


Ti )−1

× HiPi|i−1Fi

)−1

Fixi|i−1 + Pi+1|iETi+1

((Qi + FiPi|i−1F

Ti )− FiPi|i−1H

Ti

× (Ri + HiPi|i−1HTi )−1HiPi|i−1Fi

)−1FiPi|i−1H


Ti )−1

×(Zi − Hixi|i−1

). (5.78)

Na forma de blocos matriciais, esta equacao pode ser re-escrita da seguinte maneira

xi+1|i =

Pi+1|i

Ei+1

0

T


Ti


Ti

−1

Fixi|i−1

Zi − Hixi|i−1

.

(5.79)

�

5.2.1 Comparacao com a Estimativa Preditora Singular sem Robustez

Esta secao faz a comparacao entre o resultado encontrado na secao anterior e a

estimativa preditora singular sem robustez. Fazendo-se Ne,i+1 = 0, Nf,i = 0, e Nh,i = 0

nas equacoes (5.57) e (5.58) do Teorema 5.2.1. Entao

Ei+1 =

Ei+1

0

, Fi =

Fi

0

, Hi =

Hi

0

, Ri =

Ri 0

0 I

,


xi+1|i = Pi+1|i

Ei+1

0

T

×


Ti


Ti )

−1

Fixi|i−1

(zi −Hixi|i−1)

,

(5.83)

coincidindo, portanto, com a Equacao (5.24).

5.2.2 Comparacao com a Estimativa Preditora Robusta BDU

Os resultados encontrados no Teorema 5.2.1 sao agora comparados com aqueles

apresentados na referencia (SAYED (2001)), cujas deducoes foram apresentadas no

Capıtulo 3. No caso do sistema quadrado no espaco de estados, Ei+1 =[I 0

]T. Nao

se considera tambem a incerteza na matriz Hi, entao faz-se Nh,i = 0 e Ri = Ri. Assim

Pi+1|i =

(

I

0

T(

Qi 0

0 I

+

Fi√λiNf,i

Pi|i−1

[F Ti

√λiN

Tf,i

]

−

Fi√λiNf,i

Pi|i−1

[HTi 0

] (

Ri 0

0 I

+

Hi

0

Pi|i−1

[HTi 0

])−1

×

Hi

0

Pi|i−1

[F Ti

√λiN

Tf,i

])−1

I

0

)−1

=

(

I

0

T(

Qi 0

0 I

+

FiPi|i−1FTi

√λiFiPi|i−1N

Tf,i√

λiNf,iPi|i−1FTi λiNf,iPi|i−1N

Tf,i

−

FiPi|i−1HTi 0

√λiNf,iPi|i−1H

Ti 0

(

Ri 0

0 I

+

HiPi|i−1HTi 0

0 0

)−1

×

HiPi|i−1FTi

√λiHiPi|i−1N

Tf,i

0 0

)−1

I

0

)−1

(5.84)


xi+1|i = (A11 −A12A−122 A21)

I

0

T

×

(A11 −A12A−122 A21)

−1 (A11 −A12A−122 A21)

−1A12A−122

♯ ♯

Fi√λiNf,i

xi|i−1

+ (A11 −A12A−122 A21)

I

0

T

×

(A11 −A12A−122 A21)

−1 (A11 −A12A−122 A21)

−1A12A−122

♯ ♯

Fi√λiNf,i

× Pi|i−1

[HTi 0

]


0 I

−1(

zi

0

−

Hi

0

xi|i−1

)

(5.92)

ou

xi+1|i = (A11 −A12A−122 A21)

×[

(A11 −A12A−122 A21)

−1 −(A11 −A12A−122 A21)

−1A12A−122

]

×

Fi√λiNf,i

xi|i−1 + (A11 −A12A−122 A21)

×[

(A11 −A12A−122 A21)

−1 −(A11 −A12A−122 A21)

−1A12A−122

]

×

Fi√λiNf,i

Pi|i−1

[HTi 0

]


0 I

−1

×(

zi

0

−

Hi

0

xi|i−1

)(5.93)

ou


xi+1|i = Fi

(I − λi(P

−1i|i−1 +HT

i R−1i Hi + λiN

Tf,iNf,i)

−1NTf,iNf,i

)xi|i−1

+ Fi

(I − λi(P

−1i|i−1 +HT

i R−1i Hi + λiN

Tf,iNf,i)

−1NTf,iNf,i

)

× Pi|i−1

[HTi 0

]


0 I

−1(

zi

0

−

Hi

0

xi|i−1

)

(5.97)

ou

xi+1|i = Fi

(I − λi(P

−1i|i−1 +HT

i R−1i Hi + λiN

Tf,iNf,i)

−1NTf,iNf,i

)xi|i−1

+ Fi

(I − λi(P

−1i|i−1 +HT

i R−1i Hi + λiN

Tf,iNf,i)

−1NTf,iNf,i

)

× Pi|i−1HTi (Ri +HiPi|i−1H

Ti )−1(zi −Hixi|i−1). (5.98)

Como P−1i|i = P−1

i|i−1 +HTi R

−1i Hi e Pi|i = (P−1

i|i + λiNTf,iNf,i)

−1, entao

xi+1|i = Fi

(I − λiPi|iN

Tf,iNf,i

)xi|i−1 + Fi

(I − λiPi|iN

Tf,iNf,i

)

× Pi|i−1HTi (Ri +HiPi|i−1H

Ti )−1(zi −Hixi|i−1). (5.99)

Lembrando que Fc,i = Fi(I − λiPi|iNTf,iNf,i), entao

xi+1|i = Fc,ixi|i−1 + Fc,iPi|i−1HTi (Ri +HiPi|i−1H

Ti )−1(zi −Hixi|i−1). (5.100)

Comparando-se (5.100) com a expressao do filtro preditor robusto apresentado em

(SAYED (2001)) (Tabela 2), conclui-se que a diferenca entre ambas e que na Equacao

(5.100) a matriz de ponderacao Ri nao e corrigida em funcao das incertezas (veja

que em (SAYED (2001)), Ri e corrigida de acordo com a seguinte expressao Ri+1 =

Ri+1 − λ−1i Hi+1Mf,iM

Tf,iH

Ti+1).

5.2.3 Estimativa Preditora - Corretora Robusta Singular

A partir da deducao da estimativa preditora robusta singular, pode-se encontrar a

estimativa preditora-corretora robusta singular tambem.

Lema 5.2.1 A expressao para a estimativa preditora-corretora robusta para sistemas


singulares e dada por

Ei+1xi+1|i = Fixi|i. (5.101)

Prova: Explicitando-se o termo xi|i da Equacao (5.68) do Teorema 5.2.1, pode-se

expressar o termo xi|i da seguinte maneira

xi|i = xi|i−1 +[I 0

]

P−1i|i−1 + FTi Q

−1i Fi + H

Ti R

−1i Hi −F

Ti Q

−1i Ei+1


−1i Ei+1

−1

×

(HTi R−1i Zi − (FTi Q

−1i Fi + H

Ti R

−1i Hi)xi|i−1)


. (5.102)

Aplicando-se o lema da inversao de blocos matriciais, resulta

xi|i = xi|i−1 +[A−1 +A−1B(D − CA−1B)−1CA−1 −A−1B(D − CA−1B)−1

]

×

(HTi R−1i Zi − (FTi Q

−1i Fi + H

Ti R

−1i Hi)xi|i−1)


. (5.103)

Entao

xi|i = xi|i−1 +A−1(HTi R−1i Zi − (FTi Q

−1i Fi + H

Ti R

−1i Hi)xi|i−1)

+ A−1B(D − CA−1B)−1CA−1(HTi R−1i Zi − (FTi Q

−1i Fi + H

Ti R

−1i Hi)xi|i−1)

− A−1B(D − CA−1B)−1ETi+1Q−1i Fixi|i−1. (5.104)

xi|i = xi|i−1 +A−1HTi R−1i Zi −A

−1(FTi Q−1i Fi + H

Ti R

−1i Hi)xi|i−1

+ A−1B(D − CA−1B)−1CA−1HTi R−1i Zi −A

−1B(D − CA−1B)−1CA−1

× (FTi Q−1i Fi + H

Ti R

−1i Hi)xi|i−1 −A

−1B(D − CA−1B)−1ETi+1Q−1i Fixi|i−1.

(5.105)

xi|i =(I −A−1(FTi Q

−1i Fi + H

Ti R

−1i Hi)−A

−1B(D − CA−1B)−1CA−1(FTi Q−1i Fi

+ HTi R−1i Hi)−A

−1B(D − CA−1B)−1ETi+1Q−1i Fi

)xi|i−1

+ A−1(I +B(D − CA−1B)−1CA−1

)HTi R

−1i Zi. (5.106)


xi|i = A−1(A− (FTi Q

−1i Fi + H

Ti R

−1i Hi)−B(D − CA−1B)−1CA−1(FTi Q

−1i Fi

+ HTi R−1i Hi)−B(D − CA−1B)−1ETi+1Q

−1i Fi

)xi|i−1

+ A−1(I +B(D − CA−1B)−1CA−1

)HTi R

−1i Zi. (5.107)

xi|i = A−1(P−1i|i−1 − F

Ti Q

−1i Ei+1(D − CA


−1(FTi Q−1i Fi

+ HTi R−1i Hi) + FTi Q

−1i Ei+1(D − CA


)xi|i−1

+ A−1(I + FTi Q

−1i Ei+1(D −CA


−1)HTi R

−1i Zi. (5.108)

xi|i = A−1

(P−1i|i−1 + FTi Q

−1i Ei+1(D − CA


(I −A−1(FTi Q

−1i Fi

+ HTi R−1i Hi

))xi|i−1 +A−1

(I + FTi Q

−1i Ei+1(D − CA


−1)

× HTi R−1i Zi. (5.109)

xi|i = A−1

(P−1i|i−1 + FTi Q

−1i Ei+1(D − CA


−1P−1i|i−1

)xi|i−1

+ A−1(I + FTi Q

−1i Ei+1(D − CA


−1)HTi R

−1i Zi. (5.110)

xi|i = A−1

(I + FTi Q

−1i Ei+1(D − CA


−1

)P−1i|i−1xi|i−1

+ A−1(I + FTi Q

−1i Ei+1(D − CA


−1)HTi R

−1i Zi. (5.111)

Assim

xi|i−1 = Pi|i−1

(A−1 +A−1FTi Q

−1i Ei+1(D − CA


−1

)−1

xi|i

− Pi|i−1HTi R

−1i Zi. (5.112)

A expressao da estimativa preditora robusta encontrada na Equacao (5.71) pode ser

escrita como


−1i|i−1 + FTi Q

−1i Fi + H

Ti R

−1i Hi)

−1

× (HTi R−1i Zi − (FTi Q

−1i Fi + H

Ti R

−1i Hi)xi|i−1)

+ (D − CA−1B)−1ETi+1Q−1i Fixi|i−1, (5.113)



−1i|i−1 + FTi Q

−1i Fi + H

Ti R

−1i Hi)

−1

× HTi R−1i Zi − (D − CA−1B)−1ETi+1Q

−1i Fi(P

−1i|i−1 + FTi Q

−1i Fi

+ HTi R−1i Hi)


Ti R

−1i Hi)xi|i−1

+ (D − CA−1B)−1ETi+1Q−1i Fixi|i−1. (5.114)

xi+1|i = (D − CA−1B)−1ETi+1Q−1i Fi

(I − (P−1

i|i−1 + FTi Q−1i Fi

+ HTi R−1i Hi)


Ti R

−1i Hi

)xi|i−1


−1i|i−1 + FTi Q

−1i Fi + H

Ti R

−1i Hi)

−1HTi R−1i Zi

(5.115)


−1i|i−1 + FTi Q

−1i Fi + H

Ti R

−1i Hi)

−1P−1i|i−1xi|i−1


−1i|i−1 + FTi Q

−1i Fi + H

Ti R

−1i Hi)

−1HTi R−1i Zi.

(5.116)

Substituindo-se xi|i−1, Equacao (5.112), na Equacao (5.116), obtem-se


−1i|i−1

+ FTi Q−1i Fi

+ HTi R−1i Hi)

−1P−1i|i−1

(Pi|i−1

(A−1 +A−1FTi Q

−1i Ei+1(D

− CA−1B)−1ETi+1Q−1i FiA

−1)−1

xi|i − Pi|i−1HTi R

−1i Zi

)


−1i|i−1 + FTi Q

−1i Fi + H

Ti R

−1i Hi)

−1HTi R−1i Zi


−1i|i−1 + FTi Q

−1i Fi + H

Ti R

−1i Hi)

−1

×(A−1 +A−1FTi Q

−1i Ei+1(D − CA


−1)−1

xi|i

− (D − CA−1B)−1ETi+1Q−1i Fi(P

−1i|i−1 + FTi Q

−1i Fi + H

Ti R

−1i Hi)

−1HTi R−1i Zi


−1i|i−1 + FTi Q

−1i Fi + H

Ti R

−1i Hi)

−1HTi R−1i Zi


xi+1|i = (D − CA−1B)−1ETi+1Q−1i FiA

−1

×(A−1 +A−1FTi Q

−1i Ei+1(D − CA


−1)−1

xi|i

= (D − CA−1B)−1ETi+1Q−1i Fi

(I +A−1FTi Q

−1i Ei+1(D − CA

−1B)−1

× ETi+1Q−1i Fi

)−1xi|i

=(D − CA−1B + ETi+1Q

−1i FiA

−1FTi Q−1i Ei+1

)−1ETi+1Q

−1i Fixi|i

xi+1|i =(ETi+1Q

−1i Ei+1 − E

Ti+1Q

−1i FiA

−1FTi Q−1i Ei+1

+ ETi+1Q−1i FiA

−1FTi Q−1i Ei+1

)−1ETi+1Q

−1i Fixi|i

xi+1|i =(ETi+1Q

−1i Ei+1

)−1ETi+1Q

−1i Fixi|i. (5.117)

�

Como Ei+1 tem posto coluna pleno, entao

ETi+1Q−1i

(Ei+1xi+1|i − Fixi|i

)= 0, (5.118)

consequentemente

Ei+1xi+1|i = Fixi|i. (5.119)

Capıtulo 6

Matriz de Variancias para

Sistemas Singulares

Este capıtulo demonstra que as matrizes Pi+1|i+1 do Teorema 4.2.1 do Capıtulo

3, Pi+1|i do Teorema 5.2.1 do Capıtulo 4, e Pi+1|i+1 do Teorema 3.2.1 do Capıtulo

3, sao as matrizes das variancias dos erros das estimativas filtrada robusta singular,

estimativa preditora robusta singular e estimativa filtrada robusta no espaco de estados,

respectivamente.

6.1 Variancia do Erro da Estimativa Otima

Considere o seguinte lema (YU et al. (1995), sem prova).

Lema 6.1.1 Considere a estimativa de maxima verossimilhanca (ML) do vetor x base-

ado no vetor de medidas z

z = Hx+ v (6.1)

sendo v um vetor gaussiano com media zero e covariancia V . Supondo que a matriz H

tenha posto coluna pleno e[V H

]tenha posto linha pleno, entao a estimativa ML

x de x baseada nas medicoes z e dada por

λ

x

=

V H

HT 0

−1

z

0

(6.2)

88

CAPITULO 6. MATRIZ DE VARIANCIAS PARA SISTEMAS SINGULARES 89

sendo λ um vetor multiplicador de Lagrange e x = x− x o erro de estimativa dado por

λ

x

=

V H

HT 0

−1

v

0

. (6.3)

Alem disto com

V H

HT 0

−1

=

R U

UT T

(6.4)

obtem-se

E

{

λ

x

λ

x

T}

=

R 0

0 −T

. (6.5)

Em particular, quando V e invertıvel,

E{xxT } =(HTV −1H

)−1e (6.6)

E{λλT } = (I − V −1H(HTV −1H)−1HT )2V −1. (6.7)

Prova: Substituindo-se x por x+ x na Equacao (6.2), obtem-se

V H

HT 0

λ

x+ x

=

z

0

. (6.8)

Assim

V H

HT 0

λ

x

=

z

0

−

V H

HT 0

0

x

=

z

0

−

Hx

0

=

z −Hx

0

, (6.9)

portanto


V H

HT 0

λ

x

=

v

0

(6.10)

ou

λ

x

=

V H

HT 0

−1

v

0

. (6.11)

Substituindo-se (6.4) em (6.11), obtem-se

λ

x

=

R U

UT T

I

0

v

=

R

UT

v. (6.12)

Assim

E

{

λ

x

λ

x

T}

=

R

UT

E{vvT }[RT U

]

=

R

UT

V[RT U

]

=

RV RT RV U

UTV RT UTV U

. (6.13)

De acordo com (6.4), vale a seguinte expressao

V H

HT 0

R U

UT T

=

I 0

0 I

, (6.14)

entao

HTR = 0 (6.15)

V U +HT = 0 (6.16)

V R+HUT = I (6.17)


HTU = I. (6.18)

1. Pre-multiplicando-se (6.17) por RT , obtem-se

RTV R+RTHUT = RT . (6.19)

De acordo com (6.15), RTH = 0, entao

RTV R = RT , ou (6.20)

RV RT = R. (6.21)

2. Fazendo-se a transposta de (6.17), obtem-se

RTV + UHT = I. (6.22)

Pos-multiplicando-se os termos da Equacao (6.22) por U , resulta em

RTV U + UHTU = U. (6.23)

De acordo com a Equacao (6.18), HTU = I, portanto

RTV U = 0. (6.24)

Pos-multiplicando-se a Equacao (6.22) por R, obtem-se

RTV R+ UHTR = R. (6.25)

Da Equacao (6.15), tem-se que HTR = 0, portanto

RTV R = R = RT . (6.26)

Assim pode-se concluir que

RTV U = RV U = 0. (6.27)


3. Pre-multiplicando-se a Equacao (6.16) por UT , obtem-se

UTV U + UTHT = 0. (6.28)

Transpondo-se a equacao (6.28), encontra-se

UTV U + T THTU = 0, (6.29)

da equacao (6.18), segue que HTU = I, portanto

UTV U + T = 0

UTV U = −T. (6.30)

Pode-se concluir portanto, que

E

{

λ

x

λ

x

T}

=

R 0

0 −T

. (6.31)

Este resultado mostra que λ e x sao vetores Gaussianos independentes com media zero

e matrizes de variancias R e −T respectivamente. Supondo que V seja invertıvel e

usando-se o lema da inversao de blocos matriciais para inverter a matriz

V H

HT 0

,

obtem-se

V H

HT 0

−1

=

V −1 − V −1H(HTV −1H)−1HTV −1 V −1H(HTV −1H)−1

(HTV −1H)−1HTV −1 −(HTV −1H)−1

. (6.32)

Assim

λ

x

=

V −1 − V −1H(HTV −1H)−1HTV −1 V −1H(HTV −1H)−1

(HTV −1H)−1HTV −1 −(HTV −1H)−1

v

0

=

V −1 − V −1H(HTV −1H)−1HTV −1

(HTV −1H)−1HTV −1

v

(6.33)


e

E

{

λ

x

λ

x

T}

=

V −1 − V −1H(HTV −1H)−1HTV −1

(HTV −1H)−1HTV −1

E(vvT )

[V −1 − V −1H(HTV −1H)−1HTV −1 V −1H(HTV −1H)−1

]. (6.34)

Entao

E{λλT } = (I − V −1H(HTV −1H)−1HT )2V −1 e (6.35)

E{xxT } = (HTV −1H)−1. (6.36)

�

6.2 Variancia da Estimativa Otima Determinıstica

Lema 6.2.1 Considere o seguinte sistema linear

z = Hx+ v (6.37)

sendo E(vvT ) = V . Suponha que apos um experimento obteve-se uma medida z. Seja

a seguinte estimativa determinıstica

x := minx‖z −Hx‖2V −1 . (6.38)

Tem-se que

x = (HTV −1H)−1HTV −1z. (6.39)

O erro de estimativa e dado por

x = x− x = (HTV −1H)−1HTV −1v (6.40)

e a variancia do erro e dada por

P = E(xxT ) = (HTV −1H)−1. (6.41)


Prova: Considere o funcional relacionado com o problema de minimizacao (6.38)

J = ‖z −Hx‖2V −1. (6.42)

O valor otimo de x e dado por

x = (HTV −1H)−1HTV −1z. (6.43)

Com esta expressao, pode-se calcular a variancia do erro de estimativa, que e dada por

P = E(xxT ), assim

x = (HTV −1H)−1HTV −1z

= (HTV −1H)−1HTV −1(Hx+ v)

= x+ (HTV −1H)−1HTV −1v

x− x = (HTV −1H)−1HTV −1v

x = (HTV −1H)−1HTV −1v. (6.44)

Entao

P = (HTV −1H)−1HTV −1E(vvT )V −1H(HTV −1H)−1

P = (HTV −1H)−1. (6.45)

�

Lema 6.2.2 Suponha que W ≥ 0, entao as seguintes sentencas sao equivalentes

i - x ∈ argminx(Ax− b)TW (Ax− b),

ii - x = x e uma solucao de ATWAx = ATWb,

iii - (x, λ, γ) = (x, λ, γ) e uma solucao de

0 I

I W

A

0

[AT 0

]0

γ

λ

x

=

b

0

0

. (6.46)

Alem disso, para a estimativa x obtida por qualquer um dos ıtens acima tem-se


que a variancia do erro e dada por

P = E(xxT ) = (ATWA)−1. (6.47)

Prova: (i)⇒ (ii) Define-se

J = (Ax− b)TW (Ax− b)

= xTATWAx− 2xTATWb+ bTWb (6.48)

entao1

2DxJ = ATWAx−ATWb, (6.49)

portanto se x = x e um ponto de mınimo de J , deve-se ter DxJ = 0, ou

ATWAx = ATWb, (6.50)

resultando em

x = (ATWA)−1ATWb. (6.51)

(ii)⇒ (i) Como W ≥ 0, tem-se

D2xJ = ATWA ≥ 0. (6.52)

Assim se x satisfaz ATWAx = ATWb, x e um ponto de mınimo de J .

(ii)⇒ (iii) Definem-se as variaveis auxiliares

λ := b−Ax

γ := −Wλ. (6.53)

Como ATW (b−Ax) = 0, obtem-se

Ax+ λ := b

γ +Wλ := 0

ATγ = 0 (6.54)


ou

0 I A

I W 0

AT 0 0

γ

λ

x

=

b

0

0

. (6.55)

(iii)⇒ (ii)

0 I A

I W 0

AT 0 0

γ

λ

x

=

b

0

0

⇔

λ+Ax = b

γ +Wλ = 0⇒ γ = −Wλ = W (Ax− b)

AT γ = 0

De γ = W (Ax− b) tem-se ATγ = ATW (Ax− b) ⇒ 0 = ATW (Ax − b) ⇒ ATWAx =

ATWb.

(iv) - A partir do Lema 6.1.1, pode-se calcular a matriz de variancia do vetor x na

Equacao (6.55), da seguinte maneira: Seja a matriz de coeficientes da Equacao (6.55)

particionada da seguinte forma:

0 I A

I W 0

AT 0 0

=

0 I | A

I W | 0

−− −− −− −−

AT 0 | 0

. (6.56)

Identificando-se V =

0 I

I W

, H =

A

0

, HT =[AT 0

], pode-se constatar

que de acordo com o Lema 6.1.1, a matriz de variancia de x na Equacao (6.55) e dada

por

P = E(xxT ) =

([AT 0

]

0 I

I W

−1

A

0

)−1

. (6.57)

Considerando-se que

0 I

I W

−1

=

−W I

I 0

, entao

P =

(−[AT 0

]

−W I

I 0

A

0

)−1

= (ATWA)−1. (6.58)


�

6.3 Aplicacao as Estimativas Robustas Singulares

Lema 6.3.1 As seguintes sentencas sao equivalentes:

i -

x ∈ arg.minx

max{δA,δb}

{xTQx + [(A+ δA)x − (b+ δb)]TW [(A+ δA)x

− (b+ δb)]} (6.59)

sendo[δA δb

]= H∆

[Ea Eb

], ‖∆‖ ≤ 1;

ii -

x ∈ arg.minx

{xTQx +

(

A

Ea

x−

b

Eb

)T

W 0

0 λI

(.

)};(6.60)

iii -

x ∈ arg.minx

{(

I

A+ δA

x −

0

b+ δb

)T

Q 0

0 W

(.

)}(6.61)

sendo[δA δb

]= H∆

[Ea Eb

], ‖∆‖ ≤ 1;

iv -

x ∈ arg.minx

{(

I

A

Ea

x−

0

b

Eb

)T

Q 0 0

0 W 0

0 0 λI

(.

)}; (6.62)

v - (x, λ, γ) = (x, λ, γ) e uma solucao de


0 0 0 | I 0 0 | I

0 0 0 | 0 I 0 | A

0 0 0 | 0 0 I | Ea

−− −− −− −− −− −− −− −− −−

I 0 0 | Q 0 0 | 0

0 I 0 | 0 W 0 | 0

0 0 I | 0 0 λI | 0

−− −− −− −− −− −− −− −− −−

I AT ETa | 0 0 0 | 0

γ1

γ2

γ3

−−

λ1

λ2

λ3

−−

x

=

0

b

Eb

−−

0

0

0

−−

0

.(6.63)

Alem disto, para a estimativa obtida por qualquer dos itens acima, a covariancia do

erro e dada por

P = E(xxT ) =

(Q+AT WA+ λETa Ea

)−1

. (6.64)

Prova: De SAYED (2001), sabe-se que

(i)⇔ (ii) x = (Q+AT WA)−1(AT Wb+ λETa Eb) ou

x = (Q+ λETa Ea +AT WA)−1(AT W b+ λETa Eb) (6.65)

que na forma de blocos matriciais pode ser escrita como

x =

(Q+

[AT ET

a

]

W 0

0 λI

A

Ea

)−1 [

AT ETa

]

W 0

0 λI

b

Eb

.

(6.66)

De maneira compacta

x = (Q+ AT W A)−1AT W b, (6.67)

sendo A =

A

Ea

, b =

b

Eb

e W =

W 0

0 λI

. Assim


x =

([I AT

]

Q 0

0 W

I

A

)−1 [

I AT]

Q 0

0 W

0

b

. (6.68)

Usando-se o Lema 6.2.2 na Equacao (6.68), obtem-se

x ∈ arg.minx

{(

I

A

x−

0

b

)T

Q 0

0 W

(

I

A

x−

0

b

)}

= x ∈ arg.minx{xTQx+ (Ax− b)T W (Ax− b)}. (6.69)

(ii) ⇒ (v) Substituindo-se as matrizes da Equacao (6.69) na Equacao (6.55), com as

identificacoes

A←

I

A

, b←

0

b

e W ←

Q 0

0 W

, obtem-se

0 I

I

A

I

Q 0

0 W

0

I

A

T

0 0

γ

λ

x

=

0

b

0

0

(6.70)

ou

0 0 0 | I 0 0 | I

0 0 0 | 0 I 0 | A

0 0 0 | 0 0 I | Ea

−− −− −− −− −− −− −− −− −−

I 0 0 | Q 0 0 | 0

0 I 0 | 0 W 0 | 0

0 0 I | 0 0 λI | 0

−− −− −− −− −− −− −− −− −−

I AT ETa | 0 0 0 | 0

γ1

γ2

γ3

−−

λ1

λ2

λ3

−−

x

=

0

b

Eb

−−

0

0

0

−−

0

. (6.71)


(iii)⇒ (i) - Basta desfazer a formulacao matricial de (iii);

(iv) ⇒ (ii) - Basta desfazer a formulacao matricial de (iv). Com o resultado obtido

em (6.58), pode-se encontrar a matriz de variancia do erro a partir da Equacao (6.71),

fazendo-se as equivalencias

A←

I

A

Ea

e W ←

Q 0 0

0 W 0

0 0 λI

, assim

P =

([I AT ETa

]

Q 0 0

0 W 0

0 0 λI

I

A

Ea

)−1

P =

(Q+AT WA+ λETa Ea

)−1

. (6.72)

�

6.3.1 Aplicacao a Estimativa Filtrada Robusta Singular

Lema 6.3.2 Seja

xi|i+1 − xi|i

xi+1|i+1

solucao do problema de otimizacao

min{xi,xi+1}

max{δEi+1,δFi,δHi+1}


i|i (xi − xi|i)

+

(zi+1 − (Hi+1 + δHi+1)xi+1

)T

R−1

i+1

(zi+1 − (Hi+1 + δHi+1)xi+1

)

+


)T

Q−1

i


)],

(6.73)

que pode ser escrito na forma de blocos matriciais como

xi − xi|i

xi+1

T

P−1

i|i 0

0 0

xi − xi|i

xi+1

+

((

Fi Ei+1

0 Hi+1

+

δFi δEi+1

0 δHi+1

)

xi − xi|i

xi+1

−(

Fixi|i

zi+1

+

δFixi|i

0

))T

Q−1

i 0

0 R−1

i+1

(.

). (6.74)


Com[δFi δEi+1

]= Mf,i∆1,i

[Nf,i Ne,i+1

]e δHi = Mh,i∆2,iNh,i.

Tem-se que x =

xi|i+1 − xi|i

xi+1|i+1

e a estimativa ML para o seguinte sistema linear

0 0 0 | I 0 0 | I

0 0 0 | 0 I 0 | A

0 0 0 | 0 0 I | Ea

−− −− −− −− −− −− −− −− −−

I 0 0 | Q 0 0 | 0

0 I 0 | 0 W 0 | 0

0 0 I | 0 0 λI | 0

−− −− −− −− −− −− −− −− −−

I AT ETa | 0 0 0 | 0

γ1

γ2

γ3

−−

λ1

λ2

λ3

−−

x

=

0

b

Eb

−−

0

0

0

−−

0

(6.75)

sendo Q =

P−1i|i 0

0 0

, A =

Fi Ei+1

0 Hi+1

, W =

Q−1i 0

0 R−1i+1

e

Ea =

Nf,i Ne,i+1

0 Nh,i+1

e a variancia do erro de estimativa e dada por

P =

(ETi+1(Qi + FiPi|iF

Ti )−1Ei+1 + HT

i+1R−1i+1Hi+1

)−1

. (6.76)

Prova: Como Q =

P−1i|i 0

0 0

, A =

Fi Ei+1

0 Hi+1

, W =

Q−1i 0

0 R−1i+1

e

Ea =

Nf,i Ne,i+1

0 Nh,i+1

, entao substituindo-se estes valores na Equacao (6.72), obtem-

se

P =

(

P−1i|i 0

0 0

+

F Ti 0

ETi+1 HTi+1

Q−1i 0

0 R−1i+1

Fi Ei+1

0 Hi+1

+ λi

NTf,i 0

NTe,i+1 NT

h,i+1

Nf,i Ne,i+1

0 Nh,i+1

)−1

(6.77)

resultando em


P =

(

P−1i|i 0

0 0

+

FTi Q

−1i Fi FTi Q

−1i Ei+1

ETi+1Q−1i Fi E

Ti+1Q

−1i Ei+1 + HT

i+1R−1i+1Hi+1

)−1

,

(6.78)

sendo Ei+1 =

Ei+1√λiNe,i+1

, Fi =

Fi√λiNf,i

, Hi+1 =

Hi+1√λiNh,i+1

, Ri+1 =

Ri+1 0

0 I

e Qi =

Qi 0

0 I

. Assim

P =

P−1i|i + FTi Q

−1i Fi FTi Q

−1i Ei+1


−1i Ei+1 + HT

i+1R−1i+1Hi+1

−1

. (6.79)

Esta expressao representa a matriz de variancias para o vetor

xi|i+1 − xi|i

xi+1|i+1

. A

variancia do erro da estimativa filtrada, Pi+1|i+1, e dada pela expressao do bloco ma-

tricial P22 da inversa de P . Assim, admitindo-se que P−1i|i + FTi Q

−1i Fi seja invertıvel e

usando-se o Lema A.1.4, da inversao de blocos matriciais, tem-se

Pi+1|i+1 = (D − CA−1B)−1

=

(ET

i+1Q−1

i Ei+1 + HTi+1R

−1

i+1Hi+1 − E

Ti+1Q

−1

i Fi(P−1

i|i + FTi Q

−1

i Fi)−1FT

i Q−1

i Ei+1

)−1

=

(ET

i+1(Qi + FiPi|iFTi )−1Ei+1 + HT

i+1Ri+1Hi+1

)−1

, (6.80)

que e a mesma expressao encontrada em (4.41) do Teorema 4.2.1. �

6.3.2 Aplicacao a Estimativa Preditora Robusta Singular

Lema 6.3.3 Seja

xi|i−1 − xi|i

xi+1|i



min{xi, xi+1}

max{δEi+1, δFi, δHi}

[(xi|i−1 − xi)TP−1

i|i−1(xi|i−1 − xi)

+


)T

R−1

i


)

+


)T

Q−1

i


)],

(6.81)

que pode ser escrito na forma de blocos matriciais como

xi|i−1 − xi

xi+1

T

P−1i|i−1 0

0 0

xi|i−1 − xi

xi+1

+

((

Fi Ei+1

Hi 0

+

δFi δEi+1

δHi 0

)

xi|i−1 − xi

xi+1

−(

Fixi|i−1

Hixi|i−1 − zi

+

δFixi|i−1

δHixi|i−1

))T

Q−1i 0

0 R−1i

(.

).

(6.82)

Com[δFi δEi+1

]= Mf,i∆1,i

[Nf,i Ne,i+1

]e δHi = Mh,i∆2,iNh,i.

Tem-se que x =

xi|i−1 − xi|i

xi+1|i

e a estimativa ML para o seguinte sistema linear

0 0 0 | I 0 0 | I

0 0 0 | 0 I 0 | A

0 0 0 | 0 0 I | Ea

−− −− −− −− −− −− −− −− −−

I 0 0 | Q 0 0 | 0

0 I 0 | 0 W 0 | 0

0 0 I | 0 0 λI | 0

−− −− −− −− −− −− −− −− −−

I AT ETa | 0 0 0 | 0

γ1

γ2

γ3

−−

λ1

λ2

λ3

−−

x

=

0

b

Eb

−−

0

0

0

−−

0

(6.83)


sendo Q =

P−1i|i−1 0

0 0

, A =

Fi Ei+1

Hi 0

, W =

Q−1i 0

0 R−1i

e

Ea =

Nf,i Ne,i+1

Nh,i 0

e a variancia do erro de estimativa e dada por

P =

(ET

i+1(Qi + FiPi|i−1FTi − FiPi|i−1H


Ti )−1HiPi|i−1F

Ti )−1Ei+1

)−1

.

(6.84)

Prova: Como Q =

P−1i|i−1 0

0 0

, A =

Fi Ei+1

Hi 0

, W =

Q−1i 0

0 R−1i

e

Ea =

Nf,i Ne,i+1

Nh,i 0

, entao substituindo-se estes valores na Equacao (6.72) obtem-se

P =

(

P−1i|i−1 0

0 0

+

F Ti HTi

ETi+1 0

Q−1i 0

0 R−1i

Fi Ei+1

Hi 0

+ λi

NTf,i NT

h,i

NTe,i+1 0

Nf,i Ne,i+1

Nh,i 0

)−1

=

(

P−1i|i−1 0

0 0

+

FTi Q

−1i Fi + HT

i R−1i Hi FTi Q

−1i Ei+1


−1i Ei+1

)−1

, (6.85)

sendo Ei+1 =

Ei+1√λiNe,i+1

, Fi =

Fi√λiNf,i

, Hi =

Hi√λiNh,i

,

Ri =

Ri 0

0 I

e Qi =

Qi 0

0 I

. Assim

P =

P−1i|i−1 + FTi Q

−1i Fi + HT

i R−1i Hi FTi Q

−1i Ei+1


−1i Ei+1

−1

. (6.86)

Esta expressao representa a matriz de variancias para o vetor

xi|i−1 − xi|i

xi+1|i

. A

variancia do erro da estimativa preditora, xi+1|i, e dada pela expressao do bloco matri-

cial P22 da inversa de P . Assim, admitindo-se que P−1i|i−1 + FTi Q

−1i Fi + HT

i R−1i Hi seja


invertıvel e usando-se o Lema A.1.4, da inversao de blocos matriciais, obtem-se

Pxi+1|i= (D − CA−1B)−1

=

(ET

i+1Q−1

i Ei+1 − ETi+1Q

−1

i Fi(P−1

i|i−1+ FT

i Q−1

i Fi + HTi R

−1

i Hi)−1FT

i Q−1

i Ei+1

)−1

=

(ET

i+1(Qi + FiPi|i−1FTi − FiPi|i−1H


Ti )−1HiPi|i−1F

Ti )−1Ei+1

)−1

(6.87)

ou

Pi+1|i =

(

Ei+1

0

T


Ti


Ti

−1

Ei+1

0

)−1

,

(6.88)

que e igual a Equacao (5.57) do Teorema 5.2.1. �

6.4 Variancia do Erro de Estimativa do Filtro BDU

Lema 6.4.1 Seja

xi|i+1

ui+1|i


min{xi, ui}

max{δFi, δGi}


i|i (xi − xi|i) + uTi Q−1i ui

+ (zi+1 −Hi+1xi+1)TR−1

i+1(zi+1 −Hi+1xi+1)]. (6.89)

A matriz de variancia do erro de estimativa do vetor

xi|i+1

ui+1|i

e dada por

P = E

{

xi|i+1

ui|i+1

xi|i+1

ui|i+1

T}

=

Pi|i + λ2i Pi|iE

Tf,iEg,iQiE

Tg,iEf,iPi|i −λiPi|iE

Tf,iEg,iQi

−λiQiETg,iEf,iPi|i Qi

−

Pi|iFTi H

Ti+1 − λiPi|iE

Tf,iEg,iQiG

Ti H

Ti+1

QiGTi H

Ti+1

R−1e,i+1

×[

(Hi+1FiPi|i − λiHi+1GiQiETg,iEf,iPi|i) Hi+1GiQi

], (6.90)


na Equacao (6.92), obtem-se

P = E

{

xi|i+1

ui|i+1

xi|i+1

ui|i+1

T}

P =

(

P−1i|i 0

0 Q−1i

+

F Ti

GTi

HTi+1R

−1i+1Hi+1

[Fi Gi

]

+ λi

ETf,i

ETg,i

[Ef,i Eg,i

])−1

=

(

P−1i|i + λiE

Tf,iEf,i λiE

Tf,iEg,i

λiETg,iEf,i Q−1

i + λiETg,iEg,i

+

F Ti

GTi

× HTi+1R

−1i+1Hi+1

[Fi Gi

])−1

. (6.94)

Usando-se o Lema A.1.3 da inversao de blocos matriciais, obtem-se:

P−1i|i + λiE

Tf,iEf,i λiE

Tf,iEg,i

λiETg,iEf,i Q−1

i + λiETg,iEg,i

−1

=

=

Pi|i + λ2i Pi|iE

Tf,iEg,iQiE


Tf,iEg,iQi


. (6.95)

Sendo

Pi|i = (P−1i|i + λiE

Tf,iEf,i)

−1 e

Qi = (Q−1i + λiE

Tg,iEg,i − λ

2iE

Tg,iEf,i(P

−1i|i + λiE

Tf,iEf,i)E

Tf,iEg,i)

−1 ou

Qi = (Q−1i + λiE

Tg,i(I + λiEf,iPi|iE

Tf,i)

−1Eg,i)−1.

Usando-se o Lema A.1.1 da inversao de matrizes sendo

A =

P−1i|i + λiE

Tf,iEf,i λiE

Tf,iEg,i

λiETg,iEf,i Q−1

i + λiETg,iEg,i

, B =

F Ti

GTi

HTi+1,

C = R−1i+1 e D = Hi+1

[Fi Gi

],

entao pode-se re-escrever a Equacao (6.94) como


(Ri+1 +Hi+1

[Fi Gi

]

Pi|i + λ2i Pi|iE

Tf,iEg,iQiE


Tf,iEg,iQi


×

FTi

GTi

HTi+1

)−1

=

(Ri+1 +

[(Hi+1FiPi|i − λiHi+1GiQiE

Tg,iEf,iPi|i) Hi+1GiQi

]

FTi

GTi

HTi+1

)−1

=

(Ri+1 +Hi+1FiPi|iF

Ti H

Ti+1 − λiHi+1GiQiE

Tg,iEf,iPi|iF

Ti H

Ti+1 +Hi+1GiQiG

Ti H

Ti+1

)−1

=

(Ri+1 +Hi+1FiPi|iF

Ti H

Ti+1 +Hi+1GiQi(G

Ti − λiE

Tg,iEf,iPi|iF

Ti )HT

i+1

)−1

=

(Ri+1 +Hi+1FiPi|iF

Ti H

Ti+1 +Hi+1GiQiG

Ti H

Ti+1

)−1

=

(Ri+1 +Hi+1(FiPi|iF

Ti + GiQiG

Ti )HT

i+1

)−1

=

(Ri+1 +Hi+1Pi+1H

Ti+1

)−1

= R−1

e,i+1, (6.99)

sendo Pi+1 = FiPi|iFTi + GiQiG

Ti . A Equacao (6.96) pode ser escrita entao como

P =

Pi|i + λ2i Pi|iE

Tf,iEg,iQiE


Tf,iEg,iQi


−

Pi|iFTi H

Ti+1 − λiPi|iE

Tf,iEg,iQiG

Ti H

Ti+1

QiGTi H

Ti+1

R−1e,i+1

×[


]. (6.100)

A partir da Equacao (6.91), pode-se encontrar a expressao da variancia do erro do

filtro, que e dada por

E(xi+1|i+1xTi+1|i+1) =

[Fi Gi

]E

{

xi|i+1

ui|i+1

xi|i+1

ui|i+1

T}

F Ti

GTi

Capıtulo 7

Conclusoes e Continuidade do

Estudo

Esta tese apresentou no capıtulo introdutorio, conceitos detalhados dos sistemas

chamados descritores ou singulares. O Capıtulo 2 mostrou uma deducao alternativa

determinıstica para as estimativas filtrada, preditora e preditora-corretora no espaco

de estados. Mostrou tambem a relacao que existe entre a equacao de Pi+1|i+1 e Pi+1|i.

Nos demais capıtulos foram deduzidos os algoritmos recursivos das estimativas fil-

trada, suavizadora e preditora para sistemas singulares no tempo discreto, inicialmente

sem a consideracao das incertezas e depois com a consideracao delas, usando somente

a abordagem determinıstica, com a utilizacao de funcionais apropriados.

Foi possıvel tambem concluir no Capıtulo 5, que as matrizes auxiliares Pi+1|i+1 e Pi+1|i

sao respectivamente, as matrizes de variancias do erro de estimativa da estimativa

filtrada e da estimativa preditora, tanto para o sistema com robustez, como para o

sistema sem robustez. Percebe-se tambem que para os sistemas singulares nao se pode

tirar uma relacao imediata entre as matrizes Pi+1|i+1 e Pi+1|i, como ocorre no estudo

de sistemas no espaco de estados.

Como propostas para trabalhos futuros, inclusive ja iniciados, sugere-se:

• A inclusao de uma matriz Gi e sua incerteza δGi, multiplicando o ruıdo de estado.

Esta inclusao ja foi feita no artigo (CAMPOS et al. (2004)) para sistemas sem

incertezas;

112

CAPITULO 7. CONCLUSOES E CONTINUIDADE DO ESTUDO 113

• O aprofundamento do estudo da estabilidade e da convergencia para o sistema com

incertezas. Neste trabalho a estabilidade foi verificada pela analise dos autovalores

do sistema e pela convergencia da curva das normas das matrizes Pi+1|i+1 e Pi+1|i,

conforme Teorema do artigo de (SOUZA et al. (1986);

• Inclusao das incertezas nos sistemas singulares discretos nao-lineares.

Referencias Bibliograficas

BONILLA & MALABRE (2000). BONILLA, M. & MALABRE, M. (2000). More about

Non Square Implicit Descriptions for Modelling and Control. in Proc. 39th IEEE

Conf. Decision Control, Sydney, Australia, pages 3642–3647.

CAMPBELL (1982). CAMPBELL, S. L. (1982). Singular Systems of Differential Equations

II. Pitman.

CAMPOS et al. (2004). CAMPOS, J. C. T., ISHIHARA, J. Y., & TERRA, M. H. (2004).

Estimativa Recursiva Otima para Sistemas Singulares Discretos no Tempo. Anais

do XV Congresso Brasileiro de Automatica - CBA, Gramado- RS - Brasil.

DAI (1989). DAI, L. (1989). The Difference Between Regularity and Irregularity in Singular

Systems. Circuits Systems Signal Process, 8(4):435–444.

DAI (1989b). DAI, L. (1989). Filtering and LQG Problems for Discrete-Time Stochastic

Singular Systems. IEEE Trans. Automat. Contr., 34(10):1105–1108.

DAI (1989c). DAI, L. (1989). Impulsive Modes and Causality in Singular Systems. Int. J.

Control, 50(4):1267–1281.

DAI (1989d). DAI, L. (1989). Singular Control Systems. Lectures Notes in Control and

Information Sciences Series, volume 118. Springer-Verlag.

GANTMACHER (1959). GANTMACHER, F. R. (1959). The Theory of Matrices, vo-

lume II. Chelsea, New York.

GERDIN et al. (2003). GERDIN, M., GLAD, T., & LJUNG, L. (2003). A Modeling and

Filtering Framework for Linear Implicit Systems. Proceedings of the 13th IFAC

symposium on systems identification, Rotterdam, NE.

114

REFERENCIAS BIBLIOGRAFICAS 115

HASAN & AZIM-SADJANI (1995). HASAN, M. A. & AZIM-SADJANI, M. R. (1995).

Noncausal Image Modeling Using Descriptor Approach. IEEE Trans. Circuits

Syst. II, 42(8):536–540.

ISHIHARA & TERRA (2001). ISHIHARA, J. Y. & TERRA, M. H. (2001). Impulsive Con-

trollability and Observability of Rectangular Descriptor Systems. IEEE Trans.

Automat. Contr., 46(6):991–994.

ISHIHARA & TERRA (2002). ISHIHARA, J. Y. & TERRA, M. H. (2002). On the

Lyapunov Theorem for Singular Systems. IEEE Trans. on Automatic Control,

47(11):1926–1930.

KAYLATH et al. (2000). KAYLATH, T., SAYED, A. H., & HASSIBI, B. (2000). Linear

Estimation. Prentice-Hall.

LEWIS (1986). LEWIS, F. L. (1986). A Survey of Linear Singular Systems. Circ. Syst. Sig.

Proc., 5(1):3–36.

LUENBERGER (1977). LUENBERGER, D. V. (1977). Dynamic Equations in Descriptor

Form. IEEE Trans. Automat. Contr., 22(3):312–321.

MILLS & GOLDENBERG (1989). MILLS, J. K. & GOLDENBERG, A. A. (1989). Force

and Position Control of Manipulators During Constrained Motion Tasks. IEEE

Trans. Robot. Automat., 68:30–46.

NIKOUKHAH et al. (1992). NIKOUKHAH, R., WILLSKY, A. L., & LEVY, B. C. (1992).

Kalman Filtering and Riccati Equations for Decriptor Systems. IEEE Trans. Au-

tomat. Contr., 37(9):1325–1342.

SAYED (2001). SAYED, A. H. (2001). A Framework for State-Space Estimation with Un-

certain Models. IEEE Trans. Automat. Contr., AC-46(7):998–1013.

SINGH & LIU (1973). SINGH, S. P. & LIU, R. W. (1973). Existence of State Equation

Representation if Linear Large-Scale Dynamic Systems. IEEE Trans. on Circuit

Theory, 20(5):239–246.

SOUZA et al. (1986). SOUZA, C. E. D., GEVERS, M. R., & GOODWIN, G. C. (1986).

Riccati Equations in Optimal Filtering of Nonstabilizable Systems having Singular

State Transition matrices. IEEE Trans. on Automatic Control, 31:831–838.

REFERENCIAS BIBLIOGRAFICAS 116

VERGHESE et al. (1981). VERGHESE, G. C., LEVY, B. C., & KAILATH, T. (1981).

A Generalized State-Space for Singular Systems. IEEE Trans. Automat. Contr.,

26(4):811–831.

YU et al. (1995). YU, T., LIN, C. F., & MULLER, P. C. (1995). Kalman Filtering Utilizing

Future Dynamics for Descriptor Systems. Proceedings of the American Control

Conference, pages 119–123.

ZAGHLOUL & NEWCOMB (1986). ZAGHLOUL, M. E. & NEWCOMB, W. N. (1986).

Semistate Implementation: Differentiator Example. Circuits Systems, and Signal

Processing, 5(1):171–183.

ZHANG et al. (1998). ZHANG, H., CHAI, T., & LIU, X. (1998). A Unified Approach to

Optimal State Estimation for Stochastic Singular System. Automatica, 34(6):777–

781.

Apendice A

Alguns Resultados da Analise

Matricial

A.1 Alguns Resultados de Analise Matricial

Este apendice apresenta formulas da teoria de matrizes retiradas principalmente

das referencias KAYLATH et al. (2000), e GANTMACHER (1959). Algumas demons-

tracoes destas expressoes aparecem nas referencias originais e outras foram deduzidas

nesta tese.

A.1.1 Lema da Inversao de Matrizes

Lema A.1.1 Se (A + BCD) e (I + CDA−1B) sao nao-singulares e se A e uma ma-

triz n × n e tambem nao-singular e se as matrizes B, C e D sao dimensionalmente

compatıveis, entao

(A+BCD)−1 = A−1 −A−1B(I + CDA−1B)−1CDA−1.

Se alem disto, C for invertıvel, entao

(A+BCD)−1 = A−1 −A−1B(C−1 +DA−1B)−1DA−1

117

APENDICE A. ALGUNS RESULTADOS DA ANALISE MATRICIAL 118

Prova: Seja a matriz

F := A+BCD. (A.1)

Pre-multiplicando esta expressao matricial por F−1:

F−1F = F−1A+ F−1BCD = I. (A.2)

Pos-multiplicando cada lado de (A.2) por A−1:

A−1 = F−1 + F−1BCDA−1

F−1BCDA−1 = A−1 − F−1. (A.3)

Pos-multiplicando cada lado de (A.3) por B:

F−1BCDA−1B = A−1B − F−1B (A.4)

ou

A−1B = F−1B(I + CDA−1B). (A.5)

Pos-multiplicando cada lado de (A.5) por (I + CDA−1B)−1:

A−1B(I + CDA−1B)−1 = F−1B. (A.6)

Pos-multiplicando cada lado de (A.6) por CDA−1:

A−1B(I + CDA−1B)−1CDA−1 = F−1BCDA−1. (A.7)

De acordo com (A.6):

A−1B(I + CDA−1B)−1CDA−1 = A−1 − F−1 (A.8)

entao

F−1 = A−1 −A−1B(I + CDA−1B)−1CDA−1 (A.9)


e

(A+BCD)−1 = A−1 −A−1B(I + CDA−1B)−1CDA−1. (A.10)

Se a matriz C for invertıvel entao de acordo com a regra da inversa do produto de ma-

trizes o termo (I+CDA−1B)−1C de (A.10) pode ser expresso como (C−1+DA−1B)−1.

Entao obtem-se:

(A+BCD)−1 = A−1 −A−1B(C−1 +DA−1B)−1DA−1. (A.11)

�

Lema A.1.2 : Como consequencia direta do Lema A.1.1 tem-se que se A e C forem

invertıveis tem-se

(A+BC−1D)−1BC−1 = A−1B(C +DA−1B)−1 (A.12)

Prova:

(A+BC−1D)−1BC−1

= (A−1 −A−1B(C +DA−1B)−1DA−1)BC−1

= (A−1BC−1 −A−1B(C +DA−1B)−1DA−1BC−1)

= A−1B(C−1 − (C +DA−1B)−1DA−1BC−1)

= A−1B(C +DA−1B)−1. (A.13)

A.1.2 Lemas Auxiliares

Alguns destes lemas sao apresentados em KAYLATH et al. (2000) sem as com-

provacoes.

Lema A.1.3 : Para a matriz A invertıvel tem-se

A B

C D

−1

=

I −A−1B

0 I

A−1 0

0(D − CA−1B

)−1

I 0

−CA−1 I

(A.14)


e para a matriz D invertıvel tem-se

A B

C D

−1

=

I 0

−D−1C I

(A−BD−1C)−1 0

0 D−1

I −BD−1

0 I

(A.15)

Prova: Seja M =

A B

C D

uma matriz que se deseja triangularizar atraves de um

procedimento de eliminacao de Gauss. Para tanto note que

=

I 0

X I

A B

C D

=

A B

XA+ C XB +D

. (A.16)

Escolhendo-se uma matriz X tal que X = −CA−1, entao

I 0

−CA−1 I

A B

C D

=

A B

0 D − CA−1B

, (A.17)

sendo D −CA−1B chamado de complemento de Schur de A em M . Do mesmo modo,

pode-se obter

A B

C D

I −A−1B

0 I

=

A 0

C D − CA−1B

. (A.18)

Usando-se o mesmo procedimento para D invertıvel, obtem-se

I −BD−1

0 I

A B

C D

=

A−BD−1C 0

C D

(A.19)

e

A B

C D

I 0

−D−1C I

=

A−BD−1C B

0 D

, (A.20)

sendo A−BD−1C chamado de complemento de Schur de D em M . Pre-multiplicando-

se a equacao (A.18) por

I 0

−CA−1 I

obtem-se


I 0

−CA−1 I

A B

C D

I −A−1B

0 I

=

A 0

0 D − CA−1B

. (A.21)

Pos-multiplicando-se a equacao (A.20) por

I −BD−1

0 I

obtem-se

I −BD−1

0 I

A B

C D

I 0

−D−1C I

=

A−BD−1C 0

0 D

, (A.22)

assim de (A.21) resulta que

A B

C D

=

I 0

−CA−1 I

−1

A 0

0 D − CA−1B

I −A−1B

0 I

−1

, (A.23)

entao

A B

C D

−1

=

I −A−1B

0 I

A−1 0

0 (D − CA−1B)−1

I 0

−CA−1 I

(A.24)

para A invertıvel. Usando-se o mesmo procedimento chega-se a

A B

C D

−1

=

I 0

−D−1C I

(A−BD−1C)−1 0

0 D−1

I −BD−1

0 I

(A.25)

para D invertıvel. �

Lema A.1.4 : Como consequencia do Lema A.1.2, tem-se que a seguinte identidade

e valida para A invertıvel

A B

C D

−1

=

A−1 +A−1B

(D − CA−1B

)−1CA−1 −A−1B

(D − CA−1B

)−1

−(D − CA−1B

)−1CA−1

(D − CA−1B

)−1

.

(A.26)


Como tambem a seguinte identidade e valida para D invertıvel :

A B

C D

−1

=

(A−BD−1C

)−1−(A−BD−1C

)−1BD−1

−D−1C(A−BD−1C

)−1D−1 +D−1C

(A−BD−1C

)−1BD−1

.

(A.27)

Prova: Usando-se a equacao (A.24) encontra-se

A B

C D

−1

=

A−1 +A−1B

(D − CA−1B

)−1CA−1 −A−1B

(D − CA−1B

)−1

−(D − CA−1B

)−1CA−1

(D − CA−1B

)−1

(A.28)

para A invertıvel e usando-se a equacao (A.25) encontra-se

A B

C D

−1

=

(A−BD−1C

)−1−(A−BD−1C

)−1BD−1

−D−1C(A−BD−1C

)−1D−1 +D−1C

(A−BD−1C

)−1BD−1

(A.29)

para D invertıvel. �

Lema A.1.5 Sejam R ∈ Rn×n uma matriz invertıvel e A ∈ R

n×p uma matriz de posto

coluna pleno. Neste caso, ATR−1A e invertıvel e a sua inversa pode ser calculada por

(ATR−1A

)−1= −

[Ip 0

]

0 AT

A R

−1

Ip

0

= −[0 Ip

]

R A

AT 0

−1

0

Ip

, (A.30)

tem-se ainda que


(ATR−1A

)−1ATR−1 =

[Ip 0

]

0 AT

A R

−1

0

In

=[0 Ip

]

R A

AT 0

−1

In

0

(A.31)

e

R−1A(ATR−1A

)−1=[0 In

]

0 AT

A R

−1

Ip

0

=[In 0

]

R A

AT 0

−1

0

Ip

(A.32)

Prova: Como A tem posto coluna pleno, e imediato que ATR−1A seja invertıvel. Por

outro lado, pelo complemento de Schur, sabe-se que

rank

0 AT

A R

= rankR+ rank(−ATR−1A

)= n+ p

rank

R A

AT 0

= rankR+ rank(−ATR−1A

)= n+ p. (A.33)

Assim, as matrizes

0 AT

A R

e

R A

AT 0

sao invertıveis. Usando-se a equacao (A.27)

do Lema A.1.4 para a matriz D invertıvel e fazendo-se as identificacoes obvias tem-se

0 AT

A R

−1

=

(−ATR−1A

)−1 (ATR−1A

)−1ATR−1

R−1A(ATR−1A

)−1R−1 −R−1A

(ATR−1A

)−1ATR−1

(A.34)

sendo que ♯ indica que os termos, nas respectivas posicoes da matriz, nao sao import-

antes para a analise. Segue imediatamente que

(ATR−1A

)−1= −

[Ip 0

]

(−ATR−1A

)−1♯

♯ ♯

Ip0

= −[Ip 0

]

0 AT

A R

−1

Ip0

, (A.35)


(ATR−1A

)−1ATR−1 =

[Ip 0

]

♯(ATR−1A

)−1ATR−1

♯ ♯

0

In

=[Ip 0

]

0 AT

A R

−1

0

In

(A.36)

e

R−1A(ATR−1A

)−1=

[0 In

]

♯ ♯

R−1A(ATR−1A

)−1♯

Ip

0

=[0 In

]

0 AT

A R

−1

Ip0

. (A.37)

Para A invertıvel e usando-se a Equacao (A.26) do Lema A.1.4 tem-se que

(ATR−1A

)−1= −

[0 Ip

]

♯ ♯

♯(−ATR−1A

)−1

0

Ip

= −[0 Ip

]

R A

AT 0

−1

0

Ip

, (A.38)

(ATR−1A

)−1ATR−1 =

[0 Ip

]

♯ ♯(ATR−1A

)−1ATR−1 ♯

In

0

=[0 Ip

]

R A

AT 0

−1

In0

(A.39)

e

R−1A(ATR−1A

)−1=

[In 0

]

♯ R−1A(ATR−1A

)−1

♯ ♯

0

Ip

=[In 0

]

R A

AT 0

−1

0

Ip

. (A.40)

�

Apendice B

Modelagem SVD para Sistemas

Singulares

Este apendice apresenta uma forma de se obter computacionalmente a solucao para

algumas classes de sistemas singulares. Considera-se especificamente o uso de decom-

posicao em valores singulares (SVD) da matriz E do sistema. Estes resultados foram

utilizados no exemplo numerico apresentado no Capıtulo 4.

Seja o sistema linear discreto estocastico descrito por:

Ei+1xi+1 = Fixi +Biui +Giwi

zi = Hixi + vi (B.1)

sendo xi o vetor de estados de dimensao n× 1 e zi o vetor de saıda de dimensao m× 1.

O vetor de entrada u e r × 1. Ei+1 e Fi sao matrizes com dimensoes n × n. B e uma

matriz n × r e Hi e uma matriz com dimensao m× n. wi e vi sao vetores de entrada

com dimensoes n× 1 e m× 1

Fazendo-se a transformacao SVD de Ei, a primeira equacao de (B.1), fica

USV Txi+1 = Fixi +Biui +Giwi

USV Txi+1 = FiV VTxi +Biui +Giwi. (B.2)

125

APENDICE B. MODELAGEM SVD PARA SISTEMAS SINGULARES 126

Definindo xi = V Txi, entao

USxi+1 = FiV xi +Biui +Giwi

Sxi+1 = UTFiV xi + UTBiui + UTGiwi. (B.3)

Esta equacao pode ser escrita na forma matricial como

Σ 0

0 0

x1,i+1

x2,i+1

=

F11 F12

F21 F22

x1,i

x2,i

+

B1

B2

ui +

G1

G2

wi,

(B.4)

ou

Σx1,i+1 = F11x1,i + F12x2,i +B1ui +G1wi

0 = F21x1,i + F22x2,i +B2ui +G2wi. (B.5)

Se detF22 6= 0, entao esta equacao fica reduzida a

x1,i+1 = Σ−1(F11 − F12F−122 F21)x1,i + Σ−1(B1 − F12F

−122 B2)ui

+ Σ−1(G1 − F12F−122 G2)wi. (B.6)

Quanto a equacao da medida

zi = HiV VTxi + vi

zi = HiV xi + vi, (B.7)

ou

zi = H1x1,i +H2x2,i + vi. (B.8)

Considere agora o caso onde as matrizes Ei+1 e Fi tem dimensoes m× n e o posto da

matriz Ei+1 e igual a n. A partir da equacao (B.4), tem-se

APENDICE B. MODELAGEM SVD PARA SISTEMAS SINGULARES 127

Σ

0

xi+1 =

F11

F21

xi +

B1

B2

ui +

G1

G2

wi,

(B.9)

sendo F21 uma matriz com posto linha pleno. Assim

xi+1 = Σ−1F11xi + Σ−1B1ui + Σ−1G1wi (B.10)

e

0 = F21xi +B2ui +G2wi. (B.11)

Quanto a equacao da medida, ela fica sendo a mesma,

zi = HV xi + vi. (B.12)

Filtragem Robusta para Sistemas Singulares Discretos no …& GOLDENBERG (1989)), sistemas de...

Documents

Transcript of Filtragem Robusta para Sistemas Singulares Discretos no …& GOLDENBERG (1989)), sistemas de...