Response of the difference-of-Gaussians model to circular drifting-grating patches

Response of the difference-of-Gaussians modelto circular drifting-grating patches

G.T. EINEVOLL and H.E. PLESSERDepartment of Mathematical Sciences and Technology, Norwegian University of Life Sciences, Norway

(Received November 18, 2004; Accepted February 24, 2005!

Abstract

Forty years ago R.W. Rodieck introduced the Difference-of-Gaussians ~DOG! model, and this model has beenwidely used by the visual neuroscience community to quantitatively account for spatial response properties of cellsin the retina and lateral geniculate nucleus following visual stimulation. Circular patches of drifting gratings are nowregularly used as visual stimuli when probing the early visual system, but for this stimulus type the mathematicalevaluation of the DOG-model response is significantly more complicated than for moving bars, full-field driftinggratings, or circular flashing spots. Here we derive mathematical formulas for the DOG-model response to centeredcircular patch gratings. The response is found to be given as the difference between two summed series, whereeach term in the series involves the confluent hypergeometric function. This function is available in commonlyused mathematical software, and the results should thus be readily applicable. Example results illustrate how astrong surround suppression in area-summation curves for iso-luminant circular spots may be reversed into asurround enhancement for circular patch gratings. They also show that the spatial-frequency response changesfrom band-pass to low-pass when going from the full-field grating situation to the situation where the patchcovers only the receptive-field center.

Keywords: Receptive field, Difference-of-Gaussians model, Circular patches, Drifting gratings

Introduction

Forty years ago R.W. Rodieck ~1965! introduced the Difference-of-Gaussians ~DOG! model to quantitatively account for spatialreceptive-field properties in cat retinal ganglion cells. Ever since,this model has been widely applied by the neuroscience commu-nity and is now maybe the best known mathematical model invisual neuroscience. The model’s popularity stems partially fromthe mathematical simplicity of applying it: responses to differentvisual stimuli can be obtained by standard integration and simpleformulas for the stimulus dependence of responses are available inmany cases.

In the DOG model, the spatial receptive field is modeled as thedifference of two circularly symmetric and concentric Gaussians.This choice is mathematically convenient, and Rodieck was able toderive an analytical solution for the response to moving bars withthis type of receptive field. Later, Enroth-Cugell and Robson~1966! derived the spatial-frequency response for the same model,that is, the response to full-field drifting sinusoidal gratings. Thissolution is the basis for the spatial-frequency analysis methodwhich has been widely applied in the study of receptive fields thelast 25 years ~Shapley & Lennie, 1985!. Later extensions of the

Difference-of-Gaussians ~DOG! model have included temporaldelays between the center and surround Gaussians ~Enroth-Cugellet al., 1983! as well as nonconcentric ~Dawis et al., 1984! andelliptical Gaussians ~Soodak, 1986!. Even though the DOG modelwas originally suggested for retinal ganglion cells, it has also beenused to describe receptive fields in lateral geniculate nucleus~LGN! ~Kaplan et al., 1979; So & Shapley, 1981; Troy, 1983;Dawis et al., 1984; Norton et al., 1989; Mukherjee & Kaplan,1995; Uhlrich et al., 1995!.

Due to limited spatial extents of visual displays, large patchesof drifting gratings have commonly been used as a substitute forgenuine full-field gratings. As long as the patch size is larger thanthe spatial extent of the receptive field of the probed cell, theresponse will be little affected by the finite size of the grating.Lately, however, circular patches of drifting gratings of a variety ofsizes have deliberately been chosen as visual stimuli, in particularin studies of cortical feedback effects on cells in the LGN ~Sillitoet al., 1993; Cudeiro & Sillito, 1996; Sillito & Jones, 1997, 2002;Andolina et al., 2002; Allito & Usrey, 2004!.

In one set of experiments, the stimulus consisted of a circularpatch grating chosen to cover the receptive-field center of the catLGN cells in question, often in combination with a patch-gratingannulus ~with a different grating orientation! covering the surround~Sillito et al., 1993; Cudeiro & Sillito, 1996!. The purpose of theseexperiments was to study effects of cortical feedback on LGN cellresponse properties, and one motivation for using patch gratings

Address correspondence and reprint requests to: Gaute T. Einevoll,IMT, Norwegian University of Life Sciences, P.O.Box 5003, N-1432 Ås,Norway. E-mail: [email protected]

Visual Neuroscience ~2005!, 22, 437–446. Printed in the USA.Copyright © 2005 Cambridge University Press 0952-5238005 $16.00DOI: 10.10170S0952523805224057

437

instead of, say, flashing circular spots was that layer VI corticalcells providing feedback to LGN cells are more vigorously drivenby grating stimuli ~Sillito & Jones, 1997!. By selective use ofpatches and annuli of gratings covering the receptive-field centerand0or surround instead of full-field gratings, the relative contri-butions from these two parts of the receptive field could beassessed. As an example, Cudeiro and Sillito ~1996! comparedresponses to patch gratings covering the receptive-field center withresponses to full-field gratings. For LGN X cells they observedthat the characteristic band-pass spatial-frequency response for thefull-field case was changed to low-pass when the patch gratingonly covered the receptive-field center.

In other experiments, patch-grating area-summation curveshave been recorded for cat LGN cells. Here responses to circu-lar patch gratings were measured for a range of patch diametersspanning from sizes much smaller than to much larger than thereceptive-field center ~Sillito & Jones, 2002; Andolina et al.,2002!. In the area-summation curves reported by Sillito and Jones~2002!, a strong surround suppression, that is, significantlyreduced response for the largest diameters compared to the peakvalue, was observed in the normal case both for flashing spotsand their patch gratings. However, with cortical feedback re-moved, the surround suppression was found to be strongly reducedfor the patch gratings while it was essentially unaltered for flashingspots.

For patch diameters much larger than the receptive field, theresponse will correspond to the well-known full-field gratingresponse. When the patch diameter is much smaller than thewavelength of the patch grating, the stimulus is essentially asinusoidally modulated iso-luminant spot. However, in the inter-mediate regime where the patch-grating diameter, patch-gratingwavelength and spatial extent of the receptive field are compara-ble, the situation is more complicated. As for other visual stimuli,a comparison with the well-established DOG model is a naturalstrategy when interpreting patch-grating data. Such comparisonshave been pursued ~Andolina et al., 2002; Allito & Usrey, 2004!,but for circular patch-grating data encompassing this intermediateregime the mathematical evaluation of the DOG-model response issignificantly more complicated than for moving bars, full-fielddrifting gratings, or circular flashing spots.

The main purpose of this article is to derive general mathemat-ical formulas for the DOG-model response to circular patch grat-ings ~here also simply called patch gratings!. These formulas canthen immediately be used to compare and fit the DOG model toexperimental data. We show that the DOG-model response tocircular patch gratings centered at the origin of the DOG receptivefield, is given by the difference between two summed series whereeach term in the series involves the so called confluent hypergeo-metric function 1F1~a;g; x! ~Gradshteyn et al., 2000!. This is a lessfamiliar function than the Gaussian function describing the re-sponse to drifting gratings ~Enroth-Cugell & Robson, 1966! andflashing spots ~Einevoll & Heggelund, 2000!, or the error functiondescribing the response to moving bars ~Rodieck, 1965!. However,confluent hypergeometric functions are available in commonlyused mathematical software such as MATLAB and MATH-EMATICA. Our results should thus be readily applicable.

In the next section, we describe receptive fields, linear neuralresponses, and the DOG model. We then derive formulas for theDOG-model response to circular patch gratings. We further givesome example results illustrating some qualitative effects stem-ming from the interplay between the different lengths in theproblem ~patch-grating diameter and wavelength; spatial extents

of DOG center and surround!. In the final section our results aresummarized and discussed.

Receptive fields and neural responses

Impulse-response functions and linear response

For cells in the early visual pathway the response R~r, t ! to astimulus s~r, t ! can be written as

R~r, t ! ��t r0

G~r � r0,t!s~r0, t � t! dx0 dy0 dt, ~1!

if one assumes ~1! linearity, ~2! time invariance, and ~3! localspatial homogeneity. Here G~r,t! is the impulse-response function~Heeger, 1991!, s~r, t ! represents the visual stimulus presented atposition r � @x, y# at time t, and R~r, t ! is the firing rate for aneuron located at r. The spatial integral over r0 goes over alltwo-dimensional space. For mathematical convenience, we havechosen the temporal integration to go from t � �` to `. Fromcausality, it follows that G~r,t � 0!� 0, so the lower integrationboundary for t could also be set to zero.

The integral in eqn. ~1! is essentially a convolution between thestimulus and the impulse-response function, that is,

R~r, t ! � G~r, t ! * s~r, t !. ~2!

From the theory of Fourier transforms, it follows that the integralin eqn. ~1! can be reformulated as an integral over spatial andtemporal frequencies ~Bracewell, 1986!,

R~r, t ! �1

~2p!3��v k

e i ~kr�vt ! EG~k,v! Is~k,v! dkx dky dv.

~3!

Here k � @kx , ky# is the wavevector, and v is the angular fre-quency. Further, EG~k,v! and Is~k,v! are the complex Fouriertransforms of the impulse-response function G and stimulus s,respectively. The complex Fourier transform we use, and its in-verse, are given by

Iy~k,v! ��t r

e�i ~kr�vt !y~r, t ! dx dy dt, ~4!

y~r, t ! �1

~2p!3��v k

e i ~kr�vt ! Iy~k,v! dkx dky dv. ~5!

The physiological interpretation of the real-space impulse-responsefunction G~r, t ! for a particular cell is that it is given directly bythe response to test spots positioned at different positions rtest inthe receptive field of the cell. These test spots must both be verysmall @;d~r � rtest!# and narrow in time @;d~t !# . Mathematically,this corresponds to a stimulus function given by s~r, t !� Ltestd~r �rtest!d~t ! where Ltest is the luminance of the test spot. Theninsertion in eqn. ~1! yields the response R~r, t ! � LtestG~r �rtest, t ! for a neuron with the receptive field centered at r. @Here wehave used the sifting property of the d-function ~Bracewell, 1986!.#Thus, the response depends only on the difference between theposition vectors of the test spot and the receptive-field center.

438 G.T. Einevoll and H.E. Plesser

The impulse-response function is thus in principle given by themeasured firing rates of neurons at various positions r following ad-pulse at position rtest at time zero. In practice, it is easier tomeasure from a particular cell and move the test spot. Therefore,the receptive-field function is often considered instead. The impulse-response function and the receptive-field function are intimatelyrelated; the receptive-field function is the impulse-response func-tion with r replaced with �r and t with �t in the spatial andtemporal arguments, respectively ~Heeger, 1991!.

The Fourier-transformed impulse-response expression EG~k,v!also has a clear physiological interpretation. In eqn. ~3!, theresponse to the stimulus s is essentially written as an infinitesum ~integral! over contributions from drifting sinusoidal grat-ings specified by their wavevector k and angular frequency v.The wavevector is related to the spatial frequency n via 6k6 �2pn, while the angular frequency is related to the temporalfrequency f via v � 2pf. The weight and phase of each differ-ent grating required to represent the stimulus s are given byIs~k,v!. EG~k,v! tells how much a particular sinusoidal driftinggrating ~specified by k and v! contributes to the response of acell. To see this, we consider the modulatory part of a driftinggrating stimulus,

sdg~r, t ! � Cg cos~kd r � vd t !, ~6!

where kd and vd are the wavevector and angular frequency ofthe drifting grating, respectively, and Cg is a measure of thegrating contrast ~Einevoll & Plesser, 2002!. We now use thestandard mathematical trick of replacing the real functioncos~kd r � vd t ! with the complex quantity exp@i ~kd r � vd t !#and, correspondingly, the real stimulus function sdg~r, t ! with thecorresponding complex quantity sdg

c ~r, t !. These mathematicalrepresentations of the stimulus are related via sdg~r, t ! ��$sdg

c ~r, t !% where �$z% represents the real part of the complexnumber z. The Fourier transform of the ~complex! drifting grat-ing stimulus is now given by

Isdgc ~k,v! ��

t r

e�i ~kr�vt !sdgc ~r, t ! dx dy dt,

��t r

Cg ei ~kd r�vd t !e�i ~kr�vt ! dx dy dt

� Cg~2p!3d~v� vd !d

2 ~k � kd !, ~7!

where we have used the mathematical relationships

�t

e ivt dt � 2pd~v!, and

��r

e�ikr dx dy � ~2p!2d2 ~k!. ~8!

We can now insert eqn. ~7! into the response integral in eqn. ~3!.Since we use the complex stimulus sdg

c ~r, t ! instead of its realcounterpart sdg~r, t !, we obtain the complex response

Rdgc ~r, t ! �

1

~2p!3��v k

e i ~kr�vt ! EG~k,v!Cg~2p!3d~v� vd !

� d2 ~k � kd ! dkx dky dv,

� Cg EG~kd ,vd !ei ~kd r�vd t !

� Cg 6 EG~kd ,vd !6e i ~kd r�vd t�F!, ~9!

where we have used the general relationship EG ~kd ,vd ! �6 EG~kd ,vd !6e iF in the final step. The real-valued cell response isthus given by

Rdg~r, t ! � �$Rdgc ~r, t !%

� Cg 6 EG~kd ,vd !6cos~kd r � vd t �F!. ~10!

This shows that the complex Fourier-transformed impulse-responsefunction EG~k,v! gives both the amplitude of the response to adrifting sinusoidal stimulus ~6 EG~kd ,vd !6! and the phase-shift ~F!of the response compared to the sinusoidal stimulus.

Difference-of-Gaussians (DOG) model

The recipe for calculating linear responses described above appliesto any choice of receptive-field model G~r, t !. The present focus ison the Difference-of-Gaussians ~DOG! model. Following Rodieck~1965!, we assume the impulse-response function to be spatiotem-porally separable @G~r, t !� f ~r!h~t !# and model the spatial part asthe difference of two Gaussians, that is,

GDOG~r, t ! � fDOG~r!h~t !� � A1

pa12

e�r 20a12

�A2

pa22

e�r 20a22�h~t !,

~11!

where A1 and A2 ~defined to be positive! are the strengths of thecenter and surround, respectively, and a1 and a2 are correspondingwidth parameters. Rodieck ~1965! chose a particular model for thetemporal part h~t !, but here we leave it unspecified. The corre-sponding Fourier-transformed impulse response is found to be~Enroth-Cugell & Robson, 1966!

EGDOG~k,v! � DfDOG~k! Dh~v!� ~A1 e�k 2a12 04 � A2 e�k 2a2

2 04 ! Dh~v!.

~12!

With the parameters A1, A2, a1, and a2 @as well as the temporalfunction h~t !# specified, GDOG~r, t ! and EGDOG~k,v! immediatelygive the DOG-model responses to a “delta-spot” and a full-fielddrifting grating, respectively. To predict the responses to othervisual stimuli, an integral must be evaluated, and it is a matter ofconvenience whether the real-space @eqn. ~1!# or Fourier-space@eqn. ~3!# expression is used.

As a simple example, we consider the DOG-model response toflashing circular spots centered at the receptive-field center of thecell. Here a spot with diameter d is turned on at time t � 0 and kepton for a duration Dt. The mathematical expression for this stimulusis given by

sspot~r, t ! � Cs@1 �Q~r � d02!#@Q~t !�Q~t � Dt !#, ~13!

where Cs is a constant reflecting the spot luminance, and Q~x!is the Heaviside step function defined by Q~x � 0! � 0,Q~x � 0! � 1

For a neuron positioned at r � 0, the firing rate due to thisstimulus is then predicted by the DOG model to be @eqn. ~1!#

DOG model response to circular patch gratings 439

Rspot~d, t ! ��t r0

GDOG~�r0,t!sspot~r0, t � t! dx0 dy0 dt,

� Cs�0

2p�0

d02� A1

pa12

e�r02 0a1

2

�A2

pa22

e�r02 0a2

2� r0 dr0 du

� ��`

`

h~t!@Q~t � t!�Q~t � t� Dt !# dt,

� 2pCs H~t !�0

d02� A1

pa12

e�r02 0a1

2

�A2

pa22

e�r02 0a2

2� r0 dr0,

� Cs H~t !@A1~1 � e�d 204a12

!� A2~1 � e�d 204a22

!#, ~14!

where the temporal function H~t ! comes from evaluating thetemporal integral. If one is interested in the total number of actionpotentials during a time period, an integral over H~t ! must beperformed. This gives a constant which together with Cs typicallyis absorbed into redefined values of the weights A1 and A2.

DOG-model response to circular patch gratings

For a circular patch of drifting grating ~specified by kd and vd , thediameter d, and the constant Cg!, the stimulus can be mathemati-cally described as @cf. eqns. ~6! and ~13!#

spg~r, t ! � Cg @1 �Q~r � d02!# cos~kd r � vd t !. ~15!

To evaluate the DOG-model response to this stimulus, we will usethe Fourier expression in eqn. ~3!, and we thus need to evaluate theFourier transform of spg~r, t !.

Fourier expression of patch-grating stimulus

As in the full-field grating case above, it is convenient to considerthe “complex” version of the patch-grating stimulus in eqn. ~15!,that is,

spgc ~r, t ! � Cg@1 �Q~r � d02!#e i ~kd r�vd t !. ~16!

The Fourier transform of the ~complex! patch-grating stimulus isthen given by eqn. ~4!:

Ispgc ~k,v! ��

t r

spgc ~r, t !e�i ~kr�vt ! dx dy dt

��t r

Cg ei ~kd r�vd t ! @1 �Q~r � d02!#e�i ~kr�vt ! dx dy dt,

� Cg�t

e i ~v�vd !t dt ��r�d02

e i ~kd�k!r dx dy

� 2pCgd~v� vd ! ��r�d02

e�iKr dx dy, ~17!

where we have used eqn. ~8! and introduced K � k � kd tocompress the notation. The spatial integral is solved by using polarcoordinates:

��r�d02

e�iKr dx dy ��0

d02�0

2p

e�iKr cos u dur dr,

��0

d02

2pJ0~Kr!r dr �2p

K 2 �0

Kd02

J0~u!u du

�pd

KJ1~Kd02!. ~18!

Here J0~x! and J1~x! are the zeroth- and first-order Bessel func-tions, respectively, and we have used the relations ~Butkov, 1968;Bracewell, 1986!

J0~x! �1

2p�

0

2p

e�ix cos u du and

xJ0~x!�d~xJ1~x!!

dx. ~19!

When we substitute back k � kd for K, we thus find

Ispgc ~k,v! � Cg2p2d~v� vd ! d

2J1~6k � kd 6d02!

6k � kd 6d

� Cgd~v� vd !p2d 2

2S1~6k � kd 6d02!, ~20!

where we have introduced a function S1~x! defined via

S1~x! [2J1~x!

x. ~21!

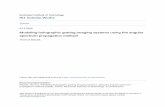
The function S1~x! is shown in Fig. 1. It has a maximum value of1 for x � 0, while its roots coincide with those of J1~x!, the firstbeing located at x � 63.832 ~Butkov, 1968!.

Typical experimental values for patch-grating spatial frequen-cies nd have been in the range 0.5–1 cycles0deg ~Sillito et al.,1993; Cudeiro & Sillito, 1996!. This corresponds to kd � 6kd 6 �2pnd in the range 3.14–6.28 deg�1. In Fig. 1, we further plotthe function S1~6k � kd 6d02! for different diameter values d forkd � 3.14 deg�1. We see that the smaller the spot diameterd, the broader the peak around kx � kd . In the limit d r `,the only contribution will come from k � kd , reflecting that thepatch grating approaches a full-field grating in this limit. InFig. 1, we finally show a contour plot of the function S1~6k �kd 6d02! for an example patch grating with a diameter of d �1.5 deg.

Fig. 1 illustrates the simple functional form of Ispgc ~k,v! in

eqn. ~20!. The diameter of the patch determines the shape of thecircularly symmetric envelope in k-space ~S1~x!! while kd deter-mines where in k-space this envelope is positioned.

Integral expressions for DOG-model response

We can now insert the result for Ispgc ~k,v! from eqn. ~20! into the

general response expression in eqn. ~3!. This gives


Rpgc ~r, t ! �

1

~2p!3��v k

e i ~kr�vt ! EG~k,v!Cgd~v� vd !

�p2d 2

2S1~6k � kd 6d02! dkx dky dv,

�Cg d 2

16pe�ivd t��

k

e ikr EG~k,vd !

� S1~6k � kd 6d02! dkx dky , ~22!

which shows that the response of the neuron will vary sinusoidallyin time with the angular frequency vd of the drifting grating insidethe patch.

The ~Fourier transformed! impulse-response function EG~k,v!of choice ~i.e., the model of choice! can now be inserted into thistwo-dimensional integral over k to obtain both the amplitude andthe phase shift of the sinusoidal modulation as a function of kd ,vd

and patch diameter d. In the general case, this integral must becomputed numerically ~Einevoll & Plesser, 2003!, but for theDOG model it can be transformed to a one-dimensional integral.

For the case where the patch and the DOG receptive field areconcentric ~r � 0!, it follows from eqns. ~12! and ~22! that thepatch-grating response is given by

Rpgc ~t ! �

Cg d 2

16pDh~vd !e

�ivd t��k

~A1 e�k 2a12 04 � A2 e�k 2a2

2 04 !

� S1~6k � kd 6d02! dkx dky . ~23!

In the Appendix we show that this response expression can betransformed to

Rpgc ~t ! � Cg Dh~vd !e

�ivd t�A1 X�a1

d, a1 kd�� A2 X�a2

d, a2 kd�� ,

~24!

where X~ y, z! is a two-dimensional function given by the one-dimensional integral

X~ y, z! � e�z 204�0

`

e�y 2x 2I0~xyz!J1~x! dx. ~25!

Here I0~x! is the zeroth-order modified Bessel function ~Abramow-itz & Stegun, 1965!.

We see that the spatial part of the expression for Rpgc ~t !

depends on four relationships between the four length scales a1,a2, d, and 10kd : a10d, a20d, a1 kd , and a2 kd . We further see thatthe response only depends on the magnitude of the spatial fre-

Fig. 1. Illustration of function S1 given in eqn. ~21! determining spatial patch-grating response in Fourier space, eqn. ~20!. Upper left:Plot of S1~x!. Upper right: Plot of S1~6k � kd 6d02! for different values of patch-grating diameters d. The graph shows the dependenceof kx when ky � 0, and kd � @kd ,0# , where kd � 3.14 deg�1. Solid curve corresponds to d � 0.5 deg, dashed to d � 1.5 deg, and dottedto d � 10 deg. Lower: Contour plot of S1~6k � kd 6d02! for d � 1.5 deg and kd � @kd ,0# with kd � 3.14 deg�1.


quency ~kd 02p! and not the orientation of the grating. This is aconsequence of the circular symmetry of the DOG model.

Series representation of DOG-model response

The function X~ y, z! given in an integral representation in eqn. ~25!can also be represented as a series. This is done by using a seriesexpansion of the modified Bessel function I0~x! in the integrand.From Abramowitz and Stegun ~1965!, we have

I0~x! � (n�0

` ~x 204!n

n!G~n � 1!� (

n�0

` ~x 204!n

~n!!2, ~26!

where we have used that G~n � 1!� n! for n � 0. We now inserta series expression for I0~xyz! into eqn. ~25! and interchange theorder of integration and summation:

X~ y, z! � e�z 204�0

`

e�y 2x 2

(n�0

` �1

4�n 1

~n!!2z 2n y2nx 2nJ1~x! dx,

� e�z 204 (n�0

` �1

4�n 1

~n!!2z 2n y2n�

0

`

e�y 2x 2x 2nJ1~x! dx.

~27!

The integral in this final expression can be found in Gradshteynet al. ~2000!:

�0

`

e�y 2x 2x 2nJ1~x! dx �

n!

4y2~n�1! 1F1~n � 1;2;�104y2 !, ~28!

where 1F1~a;g; x! is the confluent hypergeometric function givenby ~Gradshteyn et al., 2000!

1F1~a;g; x! � 1 �a

g

x

1!�a~a� 1!

g~g� 1!

x 2

2!

�a~a� 1!~a� 2!

g~g� 1!~g� 2!

x 3

3!� {{{. ~29!

For X~ y, z!, we thus have the series representation

X~ y, z! � e�z 204 (n�0

` �1

4�n 1

~n!!2z 2n y2n

n!

4y2~n�1!

� 1F1~n � 1;2;�104y2 !

� e�z 2041

4y2 (n�0

` 1

n!� z

2�2n

1F1~n � 1;2;�104y2 !, ~30!

which can be used when evaluating the DOG-model response topatch gratings using eqn. ~24!.

From the form of this series expression, it can be seen that asz r 0, fewer terms have to be included in a numerical evaluationof the series. In eqn. ~24!, it is seen that this second argument to thefunction X~ y, z! is kd a1 and kd a2, respectively, that is, propor-tional to the magnitude of the patch-grating wavevector. In the“no-grating” limit where the spatial frequency is zero, that is,kd ai � 0 ~i � 1,2!, only the first term ~n � 0! in the series ineqn. ~30! will be nonzero, and we have

X~ y,0! �1

4y2 1F1~1;2;�104y2 !, ~31!

which can be recognized as ~Abramowitz & Stegun, 1965!

1

4y2 1F1~1;2;�104y2 ! �1

4y2

e�108y 2

~�1!08y2sinh~�108y2 !

� 1 � e�104y 2. ~32!

Thus, we have X~ai 0d,0! � 1 � e�d 204ai2

~i � 1,2! in agreementwith the previous result for a ~flashing! iso-luminant spot ineqn. ~14!.

Example results

In Fig. 2, we show the spatial impulse-response function fDOG~r!and the corresponding Fourier transform DfDOG~k! of the DOGmodel considered in the following example applications.

In Fig. 3 ~upper left!, we plot area-summation curves, that is,patch-grating response @A1 X~a10d, a1 kd ! � A2 X~a20d, a2 kd !; cf.eqn. ~24!# vs. diameter for our example DOG model in Fig. 2 using

Fig. 2. Example DOG model used here with parameters A1 � 1, a1 � 0.3 deg, A2 � 0.9, and a2 � 0.6 deg. Left: DOG spatialimpulse-response function fDOG~r! in eqn. ~11! plotted along the x-axis ~ y � 0!. Right: Corresponding Fourier transformed expressionDfDOG~k! in eqn. ~12! plotted along the kx-axis ~ky � 0!.


both the series expression for X~ y, z! in eqn. ~30! and the integralexpression in eqn. ~25!. With a sufficient number of terms, theseries converges to the correct result; for this particular examplewith kd � 3.14 deg�1 five terms ~nmax � 4! are seen to besufficient to assure convergence. For larger values of kd , moreterms must be included in the series summation to obtain anaccurate numerical value for X.

In Fig. 3 ~upper right!, we show corresponding area-summationcurves for a set of different values of patch-grating wavevector mag-nitudes kd . The series expression for X~ y, z! in eqn. ~30! is used andup to 16 terms are included in the series summation for the largestconsidered value of kd . This plot illustrates the significant role playedby the wavevector magnitude kd in determining the diameter de-pendence of the patch-grating response. The area-summation curvefor the iso-luminant spot ~kd � 0, solid line! shows a strong sur-round suppression for this example model. For relatively small val-ues of kd , for example, kd � 2 deg�1 ~dashed line!, the responsecurve follows the iso-luminant spot curve closely for small diam-eters, but lies significantly above for larger diameters. The responsepeak near the receptive-field center size, d � 0.85 deg, is hardly

discernible for kd � 4.4 deg�1 ~dot-dashed line!, and it is clearlylower than the response obtained for the largest patch diameters.Thus in this case, stimulation of the surround enhances rather thansuppresses the response. For kd � 10 deg�1 the response is signif-icantly reduced all over. Even though it displays some minor os-cillations for diameters d between 0.5 and 2 deg, the response varieslittle over most of the diameter range ~d � 0.5 deg!. Fig. 3 ~lower!,showing a contour plot of the patch-grating response versus diam-eter and wavevector magnitude, highlights these points. The twomain qualitative features are immediately apparent: for large diam-eters ~d � 2 deg! the response is largest for kd;4–5 deg�1, and theiso-luminant ~kd � 0! response peak around d ; 0.85 deg is low-ered with increasing kd .

The observed strong response for large diameters for kd ; 4–5deg�1 is easily understood by looking at the Fourier-transformedreceptive field DfDOG~k! in Fig. 2 ~right!. Our example DOG modelis seen to have its maximum of DfDOG~k! at k � 4.4 deg�1, and forlarge diameters the patch grating will approach a full-field gratingwhere the response is given by DfDOG~k!. For smaller spot diam-eters, the spread in k-space around kd of the stimulus Fourier

Fig. 3. Illustration of patch-grating response @A1 X~a10d, a1 kd !� A2 X~a20d, a2 kd !; cf. eqn. ~24!# for the example DOG model in Fig. 2.Upper left: Area-summation curve, i.e., response vs. patch-grating diameter for kd � 3.14 deg�1 evaluated using the series expressionfor X in eqn. ~30! with varying series cutoff. Dotted line corresponds to the first term only, i.e., nmax � 0. Dot-dashed line correspondsto nmax � 1, dashed line to nmax � 2, and solid line to nmax � 4. The pluses correspond to results from evaluating X using the integralrepresentation in eqn. ~25! for a set of example patch-grating diameters. Upper right: Area-summation curve, i.e., response vs.patch-grating diameter d for different wavevector magnitudes kd evaluated using the series expression for X in eqn. ~30! ~summing overupto the 16 first terms in the series to assure convergence!. Solid line corresponds to kd � 0, i.e., iso-luminant spot. Dashed linecorresponds to kd � 2 deg�1, dot-dashed line to kd � 4.4 deg�1, and dotted line to kd � 10 deg�1. Lower: Contour plot of patch-gratingresponses as a function of diameter d and wavevector magnitude kd evaluated using the series expression for X in eqn. ~30! ~summingover the 16 first terms!.


transform is larger ~see Fig. 1!. Contributions to the responseintegral in eqn. ~23! will thus come from larger parts of k-spacewhere DfDOG~k! is smaller, and the band-pass peak for k � 4.4 deg�1

will become smaller and eventually vanish.The interplay between and relative contributions from the

center @A1 X~a10d, a1 kd !# and surround @A2 X~a20d, a2 kd !# termsin eqn. ~24! are illustrated in Fig. 4. Here we plot the response asa function of the magnitude of the patch-grating wavevector kd forfour different patch-grating diameters. The upper left panel corre-sponds to a large diameter, d � 3 deg, where the DOG-modelresponse essentially is identical to the full-field grating responseshown in Fig. 2 ~right!. This panel further demonstrates thewell-known and characteristic band-pass feature of the DOG model,and how it arises from subtracting the surround contribution fromthe center contribution.

The upper right panel shows the result for d � 1.5 deg corre-sponding to nearly twice the diameter of the receptive-field center.The frequency characteristic is still band-pass, but it is less prom-inent. We also see that this change mainly follows from a quali-tatively different frequency response imposed by the patch on thespatially more extended DOG surround term: the magnitude hasbeen reduced for small spatial frequencies and increased for largespatial frequencies. The contribution from the narrower DOGcenter term is much less affected.

The lower left panel of Fig. 4 shows the situation where thepatch diameter equals the receptive-field center size, d � 0.85 deg.Here the band-pass feature of the full-field grating has vanishedand has been replaced by a low-pass response characteristic, thatis, maximum for kd � 0.

The lower right panel corresponds to a very small patch diam-eter, d � 0.3 deg, where the frequency response of both the centerand surround DOG terms is dominated by the patch. The net resultis a weak response with a low-pass characteristic. In the small-diameter limit dr 0 the function S1~6k � kd 6d02! widens out andapproaches unity for all values of k, and the integral over k-spacein eqn. ~23! can be done analytically. In this limit, we find that thecontributions from the center and surround DOG terms areA1 d 204a1

2 and A2 d 204a22 , respectively, and the relative weight of

the surround compared to the center term is thus A2 a12 0A1 a2

2. Forthe example DOG model in the figure, this ratio is 0.225. This isnot too different from the numerical value 0.247 found for kd � 0for the small ~but not infinitely small! diameter value d � 0.3 degconsidered in the lower right panel of Fig. 4.

The upper right and lower left panels of Fig. 4 also illustratethat center and surround responses to patch gratings can switchsign ~corresponding to a 180 deg phase change of the oscillatingresponse! when stimulus parameters are varied. In the upper rightpanel ~d � 1.5 deg!, the contribution from the surround @A2 X~a20

Fig. 4. Illustration of patch-grating responses @A1 X~a10d, a1 kd ! � A2 X~a20d, a2 kd !; cf. eqn. ~24!# ~solid line! as a function ofmagnitude of grating wavevector for four different patch diameters for the DOG model in Fig. 2. Contributions from the center@A1 X~a10d, a1 kd !# ~dashed line! and surround @A2 X~a20d, a2 kd !# ~dot-dashed line! are also shown. Upper left: Patch-grating diameterd � 3 deg. Upper right: d � 1.5 deg. Lower left: d � 0.85 deg, corresponding to the size of the receptive-field center. Lower right:d � 0.3 deg.


d, a2 kd !# is seen to be negative for kd in the range ;7–10 deg�1.Likewise, the total DOG-model response becomes ~barely! nega-tive for kd ; 18–20 deg�1. The sign switch of the surroundcontribution for kd ; 7–10 deg�1 can be understood mathemati-cally by considering the response integral expression in eqn. ~23!.For d � 1.5 deg and kd; 7–10 deg�1, there will be relatively littleoverlap between the positive central lobe of S1~6k � kd 6d02! andthe surround Gaussian @A2 exp~�k 2a2

2 04!# ~cf. Fig. 1 ~upper right,dashed line! and Fig. 4 ~upper left, dot-dashed curve!!. However,the first negative lobe of S1~6k � kd 6d02! will overlap substan-tially with the surround Gaussian, and as a consequence the spatialintegration over k-space will end up giving a negative number.

Compared to the full-field grating situation in the upper leftpanel of Fig. 4, we see that the patch-grating data in the otherpanels have a larger high-frequency cutoff. The relative weight ofthe high frequencies will be largest for smaller patch gratingswhere S1~6k � kd 6d02! has the largest extension in k-space. Thenthe spatial integral in eqn. ~23! can become nonnegligible evenwhen kd is larger than the high-frequency cutoff for the full-fieldgrating case.

Fig. 4 further illustrates that with patch gratings stimulation ofthe surround does not necessarily reduce the response compared tostimulation of only the receptive-field center. By comparison of theresults in the upper left and lower left panels, we can infer that forkd in the range ;3.5–8 deg�1 the full-field grating response, thatis, center plus surround, is in fact larger than the response fromstimulating only the receptive-field center. Such a wavevector-dependent transition between surround suppression and surroundenhancement for patch gratings was observed for an LGN X cellreported by Cudeiro and Sillito ~1996, Fig. 2!.

Discussion

The main result of this article is the mathematical formula for theDOG-model response to centered circular patch gratings in termsof two summed series. From eqns. ~24! and ~30!, we have that thespatial part of this response is given by

ERpg~d,n! � A1 X�a1

d,2pa1nd�� A2 X�a2

d,2pa2nd�,

X~ y, z! � e�z 2041

4y2 (n�0

` 1

n!� z

2�2n

1F1~n � 1;2;�104y2 !, ~33!

where nd and d are the spatial frequency and diameter of thecircular patch grating, respectively, and A1, a1, A2, and a2 areDOG-model parameters.

This formula encompasses two well-known limiting cases:full-field drifting grating and iso-luminant ~flashing! spot. A full-field grating is obtained in the large-diameter limit dr `, wherethe response expression is given by @cf. eqn. ~12!#

ERdg~nd ! � A1 e�p 2nd2 a1

2

� A2 e�p 2nd2 a2

2

. ~34!

An iso-luminant spot is obtained in the zero spatial-frequency limitndr 0, and in this case the response is given by @cf. eqns. ~14! and~32!#

ERspot~d ! � A1~1 � e�d 204a12

!� A2~1 � e�d 204a22

!. ~35!

Each term in the series representation for X~ y, z! in eqn. ~33!involves the confluent hypergeometric function 1F1 ~Gradshteyn

et al., 2000!. Although unfamiliar to some, this special function isavailable in commonly used mathematical software such as MAT-LAB and MATHEMATICA. Application of this formula for com-parison and fitting of the DOG model to experimental data shouldtherefore be straightforward.

The contour plot in Fig. 3 ~lower! for our example DOG modelillustrates that the interplay between the four length constants inthe system ~DOG spatial widths a1, a2, patch-grating diameter d,patch-grating wavelength 2p0kd ! can give a variety of qualita-tively different response characteristics even for the simple DOGmodel.

One characteristic feature is the dependence of the surroundsuppression in area-summation curves ~response vs. patch diam-eter! on the patch-grating wavevector. In Fig. 3 ~upper right!, weobserved in our example model a significant surround suppressionfor the iso-luminant spot, less so for kd � 2 deg�1, while for kd �4.4 deg�1 a surround enhancement was observed. This featureagrees qualitatively with the observation for decorticated LGNcells by Sillito and Jones ~2002! where a significant reduction ofsurround suppression was seen for patch gratings compared toflashing spots.

Another characteristic feature is the transition from the full-field band-pass response to a low-pass response when the patchdiameter equals the receptive-field center size ~cf. Fig. 4!. This isin qualitative agreement with experimental observations of catLGN X cells in Cudeiro and Sillito ~1996, Fig. 4!.

While two length constants ~d,2p0kd ! characterize the patch-grating stimulus, full-field drifting gratings and flashing spots arecharacterized by only a single length constant ~2p0kd and d,respectively!. Thus, as demonstrated here a richer set of qualita-tively different response characteristics can be obtained for patchgratings, and this can be helpful when probing the system. If suchexperiments are pursued and a comparison with the DOG model iswanted, the necessary mathematical apparatus is provided here.

Acknowledgment

Support from Honda Research Institute Europe is gratefully acknowledged.

References

Abramowitz, M. & Stegun, I.A. ~1965!. Handbook of MathematicalFunctions. New York: Dover.

Allito, H.J. & Usrey, W.M. ~2004!. Temporal evolution of extra-classicalsuppression in the LGN: Distinguishing feedforward and feedbackmechanisms. Society for Neuroscience Abstracts 409.5.

Andolina, I.M., Wang, W., Jones, H.E., Salt, T.E. & Sillito, A.M.~2002!. Effects of feedback on cat LGN cell spatial summation param-eters dissected with the difference of Gaussian model ~DOGM!. Soci-ety for Neuroscience Abstracts 352.17.

Bracewell, R.N. ~1986!. The Fourier Transform and its Applications.New York: McGraw-Hill.

Butkov, E. ~1968!. Mathematical Physics. New York: Addison-Wesley.Cudeiro, J. & Sillito, A.M. ~1996!. Spatial frequency tuning of orientation-

discontinuity-sensitive corticofugal feedback to the cat lateral genicu-late nucleus. Journal of Physiology 490, 481–492.

Dawis, S., Shapley, R., Kaplan, E. & Tranchina, D. ~1984!. Thereceptive field organization of X-cells in the cat: Spatiotemporal cou-pling and asymmetry. Vision Research 24, 549–564.

Einevoll, G.T. & Heggelund, P. ~2000!. Mathematical models for thespatial receptive-field organization of nonlagged X cells in dorsallateral geniculate nucleus of cat. Visual Neuroscience 17, 871–886.

Einevoll, G.T. & Plesser, H.E. ~2002!. Linear mechanistic models forthe dorsal lateral geniculate nucleus of cat probed using drifting-gratingstimuli. Network: Computation in Neural Systems 13, 503–530.

Einevoll, G.T. & Plesser, H.E. ~2003!. Extended DOG receptive-fieldmodel for LGN relay cells incorporating cortical-feedback effects.Society for Neuroscience Abstracts 68.11.


Enroth-Cugell, C. & Robson, J.G. ~1966!. The contrast sensitivity ofretinal ganglion cells of the cat. Journal of Physiology 187, 517–552.

Enroth-Cugell, C., Robson, J.G., Schweitzer-Tong, D.E. & Watson,A.B. ~1983!. Spatio-temporal interactions in cat retinal ganglion cellsshowing linear spatial summation. Journal of Physiology 341, 279–307.

Gradshteyn, I.S., Ryzhik, I.M. & Jeffrey, A. ~2000!. Tables of Inte-grals, Series and Products. New York: Academic Press.

Heeger, D.J. ~1991!. Nonlinear model of neural responses in cat visualcortex. In Computational Models of Visual Processing, ed. Landy,M.S. & Movshon, J.A., pp. 119–134. Cambridge, Massachusetts: MITPress.

Kaplan, E., Marcus, S. & So, Y.T. ~1979!. Effects of dark adaptation onspatial and temporal properties of receptive fields in cat lateral genic-ulate nucleus. Journal of Physiology 294, 561–580.

Mukherjee, P. & Kaplan, E. ~1995!. Dynamics of neurons in the catlateral geniculate nucleus: In vivo electrophysiology and computationalmodeling. Journal of Neurophysiology 74, 1222–1243.

Norton, T.T., Holdefer, R.N. & Godwin, D.W. ~1989!. Effects ofbicuculline on receptive field center sensitivity of relay cells in lateralgeniculate nucleus. Brain Research 488, 348–352.

Rodieck, R.W. ~1965!. Quantitative analysis of cat retinal ganglion cellresponse to visual stimuli. Vision Research 5, 583–601.

Shapley, R. & Lennie, P. ~1985!. Spatial frequency analysis in the visualsystem. Annual Review of Neuroscience 8, 547–583.

Sillito, A., Cudeiro, J. & Murphy, P. ~1993!. Orientation sensitiveelements in the corticofugal influence on centre-surround interactionsin the dorsal lateral geniculate nucleus. Experimental Brain Research93, 6–16.

Sillito, A. & Jones, H.E. ~1997!. Functional organization influencingneurotransmission in the lateral geniculate nucleus. In Thalamus, Vol.II, ed. Steriade, M., Jones, E.G. & McCormick, D.A., pp. 1–52.Amsterdam: Elsevier.

Sillito, A.M. & Jones, H.E. ~2002!. Corticothalamic interactions in thetransfer of visual information. Philosophical Transactions of the RoyalSociety B ~London! 357, 1739–52.

So, Y.T. & Shapley, R. ~1981!. Spatial tuning of cells in and around lateralgeniculate nucleus of the cat: X and Y relay cells and perigeniculateinterneurons. Journal of Neurophysiology 45, 107–120.

Soodak, R.E. ~1986!. Two-dimensional modeling of visual receptive fieldsusing Gaussian subunits. Proceedings of the National Academy ofSciences of the U.S.A. 83, 9259–9263.

Troy, J.B. ~1983!. Spatial contrast sensitivities of X and Y type neuronesin the cat’s dorsal lateral geniculate nucleus. Journal of Physiology 344,399–417.

Uhlrich, D.J., Tamamaki, N., Murphy, P.C. & Sherman, S.M ~1995!.Effects of brain stem parabrachial activation on receptive field prop-erties of cells in the cat’s lateral geniculate nucleus. Journal of Neuro-physiology 73, 2428–2447.

Appendix

In this Appendix, we show that the patch-grating response expression ineqn. ~23! involving a two-dimensional integral can be transformed to theexpression in eqn. ~24!, where X~ y, z! is given by the one-dimensionalintegral expression in eqn. ~25!. This amounts to showing that

��k

e�k 2a204d 2

16pS1~6k � kd 6d02! dkx dky � X~a0d, akd !. ~36!

From the definition of S1~x! in eqn. ~21!, it follows that the left side ofeqn. ~36!, labeled I, is given by

I ��k

e�k 2a204d 2

16p

2J1~6k � kd 6d02!

6k � kd 6d02dkx dky

��k

e�k 2a204 dJ1~6k � kd 6d02!

4p6k � kd 6dkx dky . ~37!

We introduce K � k � kd and change the integration variable from k to K,and obtain

I ��K

e�6K�kd 62a204 d

J1~Kd02!

4pKdKx dKy

��V

e�6V�vd 62a20d 2

J1~V !

2pVdVx dVy , ~38!

where we in the last step have introduced the dimensionless variables V �Kd02 and vd � kd d02. We further introduce the dimensionless parametery � a0d as well as polar coordinates for V:

I ��0

`�0

2p

e�~V 2�vd2�2Vvd cos u!y 2

J1~V !

2pVV dV du

� e�vd2 y 2�

0

`

e�V 2 y 2��0

2p

e�2Vvd y 2 cos u du� J1~V !

2pdV

� e�vd2 y 2�

0

`

e�V 2 y 2I0~2Vvd y2 !J1~V ! dV. ~39!

Here we have introduced the modified Bessel function I0~x! by use of therelation ~Abramowitz & Stegun, 1965!

I0~x! �1

2p�

0

2p

e6x cos u du. ~40!

With another dimensionless parameter z � akd � dykd � 2yvd, we can writethe final integral as

I � e�z 204�0

`

e�V 2 y 2I0~Vyz!J1~V ! dV ~41!

which is identical to X~ y, z! in eqn. ~25!.


Response of the difference-of-Gaussians model to circular drifting-grating patches

Documents

Transcript of Response of the difference-of-Gaussians model to circular drifting-grating patches