Structural and magnetic study of La0.7Sr0.3MnO3 nanoparticles and ACmagnetic heating characteristics for hyperthermia applications

D.H. Manh b, P.T. Phong a,n, P.H. Namb, D.K. Tung b, N.X. Phuc b, In-Ja Lee a,n

a Department of Advanced Materials Chemistry, Dongguk University-Gyeongju, 707 Suckjang-dong, Gyeongju-Si 780-714, Gyeongbuk, Koreab Institute of Materials Science, Vietnam Academy of Science and Technology, 18 Hoang Quoc Viet Road, Cau Giay District, Ha Noi City, Viet Nam

a r t i c l e i n f o

Article history:Received 5 January 2014Received in revised form12 March 2014Accepted 12 March 2014Available online 21 March 2014

Keywords:La0.7Sr0.3MnO3 nanoparticlesSuperparamagneticAC-lossesHyperthermiaIntrinsic loss power

a b s t r a c t

We investigated structural and magnetic properties and alternating current magnetic heating character-istics of La0.7Sr0.3MnO3 nanoparticles with respect to the possible application for magnetic hyperthermiatreatments. Using Rietveld Profile refinement of powder X-ray diffraction data, the hexagonal structurehas been observed. The particle sizes varied from 20 to 50 nm as the annealing temperature increasesfrom 700 to 900 1C. The hysteresis loop is not observed and the good fit of Langevin function withmagnetization data reveals the superparamagnetic nature at room temperature for all samples.Characteristic magnetic parameters of the particles including saturation magnetization in the tempera-ture range 10–300 K, an effective anisotropy constant and a magnetocrystalline anisotropy constant havebeen determined. The Specific Absorption Rate for 15 mg/mL sample concentration was measured inalternating magnetic fields of 50–80 Oe at a fixed frequency of 236 kHz. In addition, the intrinsic losspower (ILP) has been calculated from SAR values. It is believed that La0.7Sr0.3MnO3 nanoparticles with ahigh ILP will be useful for the in situ hyperthermia treatment of cancer.

& 2014 Elsevier B.V. All rights reserved.

1. Introduction

In recent years, magnetic nanoparticles (MNPs) have been usedin magnetic hyperthermia, referring to the introduction of ferro-magnetic or superparamagnetic particles into the tumor tissue [1].The MNPs create heat that can be used to treat cancer when theyare placed in alternating magnetic fields. To destroy malignantcells by means of heat treatment, the MNPs are injected into thetumors and excited by an applied AC magnetic field. By this, theMNPs generate heat inside the tumor. If the temperature reachesup to 43–45 1C, the cancer cells can be irreversibly destroyed whilehealthy tissues remain unaffected (without MNPs). For moreeffective therapeutic treatments, materials with highly saturatedmagnetization, such as transition metals (e.g. Fe, Co, and Ni) ormetal oxides (e.g. Fe3O4 and g-Fe2O3), are usually considered.Although pure metals possess the highest saturation magnetiza-tion, they are highly toxic and extremely sensitive to oxidation [2];therefore, without appropriate additional surface treatment suchpure metal nanoparticles are not suitable for biomedical applica-tions [3]. On the contrary, a large number of studies have shownthat magnetite and maghemite nanoparticles are less sensitive tooxidation and, therefore, can be very promising candidates due to

their biocompatibility and relative ease to functionalize [4]. In fact,the magnetic materials will provide more heating in the ferro-magnetic state (below Curie temperature—TC), and vice versa, lessheating in paramagnetic state (above TC). Thus the Curie tempera-ture acts as a temperature controlled switch and upholds aconstant desired temperature in the tumor region [5].

Up to now, a wide range of ferromagnetic nanoparticles,including metals/alloys with superior magnetic properties andsuitable TC, have been synthesized for use in magnetic fluidhyperthermia [6–9]. Among them, the La0.7Sr0.3MnO3 (LSMO)nanoparticles are one of the best candidates for self-controlledhyperthermia applications because not only did they have highermagnetic moment at room temperature than that of most for suchapplications, but also their Curie temperature can be easilyadjusted between 315 and 350 K [10–12].

La0.7Sr0.3MnO3 nanoparticles can be synthesized by variousmethods such as co-precipitation, sol–gel, hydrothermal techni-que, microwave refluxing technique, solution combustion, solidstate reaction and high energy ball milling [13–16]. Among them,the high energy ball milling combined with the thermal proces-sing method is a promising alternative synthetic method, due toits ability to alter grain size at a much lower temperature [16].

In the present work, LSMO MNPs were prepared by the highenergy ball milling combined with the thermal processingmethod. The structural and magnetic properties of NPs wereinvestigated to understand their self-heating mechanism in theAC magnetic field. Each of the composite samples was exposed to

Contents lists available at ScienceDirect

journal homepage: www.elsevier.com/locate/physb

Physica B

http://dx.doi.org/10.1016/j.physb.2014.03.0250921-4526/& 2014 Elsevier B.V. All rights reserved.

n Corresponding authors. Tel./fax: þ82 54 7702220.E-mail addresses: ptphong.nh@khanhhoa.edu.vn (P.T. Phong),

lij@dongguk.ac.kr (I.-J. Lee).

Physica B 444 (2014) 94–102

a 236 kHz alternating magnetic field of amplitude 50–80 Oe and asignificant heating effect was observed in all samples. In addition,the intrinsic loss power (ILP) has been obtained from the SpecificAbsorption Rate (SAR) values. The higher ILP values of our samplesare comparable to those of La1�xSrxMnO3 (0.15rxr0.45) [5] andcommercial ferrofluids [17], which suggests potential for use inmagnetic hyperthermia.

2. Experimental

The nanopowder sample La0.7Sr0.3MnO3 with size in the rangeof 20–50 nm has been prepared using reactive milling combinedwith thermal processing methods. In the reactive milling method,high purity (99.9%) La2O3, MnO2 and SrCO3 were weighed in thedesired proportion according to the following reaction:

0:72La2O3þ0:3SrCO3þMnO2-La0:7Sr0:3MnO3þ

0:74O2þ0:3CO2

The mixture of high purity powders was ground for 8 h in acommercial high energy SPEX 8000D shaker mill. The powderswere put in vial with 2.5 in. and 4.25 in. balls. The vial and theballs were made of tempered steel. Single phase LSMO nanopow-ders have been obtained after 8 h of milling in the ambientatmosphere [18]. Finally, the resulting powders were annealed at700 1C, 800 1C and 900 1C for 3 h in air. In this report, we refer tothe sample sintered at 700 1C, as S1, that sintered at 800 1C as S2and sample sintered at 900 1C as S3. Phase purity, homogeneity,and crystal structure were characterized by X-ray powder diffrac-tion using a SIEMENS D 5000 diffractometer with CuKα radiation(λ¼1.5406 Å). The data were obtained at room temperature in the2θ range of 20–801 with step size of 0.021 with a scanning rate of21/min. The X-ray powder diffraction patterns were evaluatedusing a commercial X'pert Highscore Plus of PANalytical programfor the Rietveld refinement analysis [19]. The surface morphologyof the samples was observed using scanning electron microscopy(SEM). The magnetization measurements were performed on aQuantum Design PPMS-6000 to determine the saturation magne-tization (Ms), blocking temperature (TB) and Curie temperature(TC). The measurements include (i) zero-field cooling (ZFC) andfield cooling (FC) taken in the temperature range 80–420 K atapplied magnetic field of 100 Oe and (ii) field dependent magne-tization, (M–H), in the range 10–300 K with magnetic applied fieldup to 6 T. In order to investigate the Specific Absorption Rate ofLSMO nanoparticles for hyperthermia application, induction heat-ing was performed in a homemade radio frequency power supply,which was connected to an induction coil [20]. A generator (RDOHFI 5 kW) was used to create an alternating magnetic field ofamplitude from 50 Oe to 80 Oe at a frequency of 236 kHz. Theferrofluid prepared by dispersing 15 mg LSMO in 1 ml of deionizeddistilled water was put in a glass vessel which was insulated usinga teflon coating shell [21]. The temperature rise was recorded as afunction of time up to 30 min.

3. Results and discussion

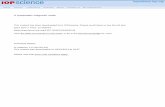
The XRD results for the whole samples are shown in Fig. 1. TheRietveld fitting of the pattern shows that the crystal structure ofLSMO nanopowder is of the hexagonal type with R-3CH spacegroup at room temperature in which the La/Sr atoms are located at6a (0, 0, 1/4) position, Mn atoms at 6b (0, 0, 0), and oxygen atomsat 18e (x, 0, 1/4) positions. The Mn atom is coordinated by sixoxygen atoms forming MnO6 octahedra. The refined parametersobtained are presented in Table 1. In the previously reportedpapers, different structures such as cubic, orthorhombic, mono-clinic, and rhombohedral have been observed for LSMO compound.

The hexagonal structure at room temperature has been observedfor the first time by Bindu [22]. We have also presented theMn–O–Mn bond angle and Mn–O bond length for the bulk samplein Table 1 for comparison. Our results are close to those obtainedby Bindu [22] for LSMO sample synthesized using the standardsolid-phase reaction.

The particle sizes of the synthesized samples were calculatedusing the Hall–Williamson method [23]:

β cos θ¼ 0:89λD

þ4ε sin θ ð1Þ

where λ is the wavelength of the X-ray radiation (λ¼0.1546 nm),θ is Bragg's angle, β is the full width at half-maximum (FWHM)of (1 1 0) peak, and ε is the internal strain. The particle sizeswere found to be 20, 30, and 50 nm for samples S1, S2, and S3,respectively. It is clearly seen that the particle sizes increase withincreasing annealing temperature. Under the assumption thatmost particles exist in a spherical shape, the specific surface area(As) can be estimated using formula

As ¼6Dρ

ð2Þ

where D is the particle diameter and ρ is the theoretical densityof LSMO (6.45 g/cm3). As the grain size decreases, because of thehigher surface to volume ratio for smaller particles, increase in thespecific surface area is observed (see Table 1). It is known thatthe critical diameter (dc) below which particles have a singlemagnetic domain particle is given by [24]

dc ¼18

ffiffiffiffiffiffiffiffiffiffiffiAexK

pμ0M

2s

ð3Þ

where AexE10�11 J m�1 is the exchange stiffness, K the uniaxialanisotropy constant, μ0 the vacuum permeability, and Ms thesaturation magnetization. The critical diameter depends on the

20 30 40 50 60 70 80

S1S2S3

inte

nsity

(a.u

.)

(012

)

(122

), (1

16)(024

)

(113

), (2

02),

(006

)(110

), (1

04)

(030

), (2

14),

(018

)

(134

), (1

28)

(220

), (2

08)

(036

), (1

010)

2 (degree)θ

Fig. 1. Room temperature XRD patterns of S1, S2, and S3.

Table 1Lattice parameters, unit cell volume, particle size and specific surface area forLa0.7Sr0.3MnO3 nanoparticles.

Sample a (Å) c (Å) V (Å3) θMn–O–Mn

(deg)dMn–O

(Å)W(10�2)

D(nm)

As

(m2 g�1)

S1 5.494 13.384 349.91 166.33 1.955 9.504 20 46.51S2 5.498 13.388 350.47 166.328 1.954 9.521 30 31.07S3 5.503 13.390 351.19 166.325 1.953 9.534 50 18.61Bulka 5.508 13.357 350.95 166.9 1.954

a Ref. [22].

D.H. Manh et al. / Physica B 444 (2014) 94–102 95

material, but it is normally in the range 5–1000 nm. For example,the critical diameter is about 6 nm for Fe, 60 nm for Fe3O4 [24],80 nm La0.7Ca0.3MnO3 [25] and about 70 nm for La0.7Sr0.3MnO3

[26]. Although in a real system, the distribution of particle sizes ispolydisperse in nature, the reasonably narrow distribution ofparticle sizes in our samples indicates that the maximum particlesize is not expected to cross 70 nm. Thus, we can assign the natureof the physical structure of our samples to be the assemblies ofsingle domain particles. Moreover, superparamagnetic behaviorshould be expected in these single domain systems.

The detailed surface morphologies of the samples were mea-sured by FE-SEM and the corresponding images for all samples arepresented in Fig. 2. From the image one can observe that samplesconsisted of agglomerated nanoparticles and most of the grainsare spherical in shape. It is further observed that the grain size inthe samples is distributed in the range of 20–50 nm. In addition,the particle size increases with increase in annealing temperature.

Fig. 3 shows the variation of magnetization M as a function oftemperature (T) of three samples at 100 Oe and the temperaturerange 80–420 K recorded in zero-field-cooled (ZFC) and field-cooled (FC). The Curie temperature (defined as one correspondingto the peak of dMZFC/dT) is 346, 356 and 360 K for samples S1, S2and S3, respectively. Obviously, the Curie temperature (TC) sharplyincreases with change in the sample from S1 to S2, and thenslightly increases for S3. It indicates that as close to the criticalvalue of the particle size (70 nm), TC is almost unaffected byparticle size, which is close to TC (365 K) of bulk manganites withthe same composition [27]. In samples S2 and S3, grain size hasonly a small effect on the TC values; this is in good agreement withpreviously reported paper [26]. The TC values (369, 367, and 362 K)for the La0.67Sr0.33MnO3 manganite samples with particle sizes ofabout 85, 51, and 32 nm, and an increase in the TC value withincrease in the particle size have been reported by Lu et al. [28]. Onthe other hand, the magnetization (M) decreases as particle getssmaller, which is in agreement to that obtained by Sánchez et al.[29], in which both magnetization and TC decrease with decreasingparticle size of La0.67Ca0.33MnO3 in the range 30–70 nm. Aninteresting feature is that all samples exhibit large separation

between MFC and MZFC curve below magnetic irreversible tem-perature (Tirr) which is related to the presence of strong magneticanisotropy. Moreover, as can be seen in the inset, the samplesshow either a typical superparamagnetic blocking process orcooperative freezing of particle moments at Tmax. Most interest-ingly, with increase in particle size from 20 to 50 nm, Tmax shiftstowards the higher temperature side from 265 to 277 K. In oursystem, no magnetic relaxation was observed below Tmax; hencethe spin glass behavior does not exist and the system can beconsidered both the single domain and superparamagnetic innature. However, to gain a deeper understanding of the super-paramagetic characteristic of samples, we will further discuss thisissue later.

To explain the reduction of TC described above, we consider thedistribution of double exchange (DE) interaction. Since the mag-netic and transport properties of these manganites stronglydepend on both the Mn–O–Mn bond angle and Mn–O bonddistance, decrease in bond angle and increase in bond length tendto reduce the DE interaction which leads to a lower ordering TC. Inaddition, this reduction can be explained using the empiricalformula of the bandwidth W for ABO3-type perovskites [30]

W ¼ cos ½1=2ðπ�γÞ�ðdMn–OÞ3:5

ð4Þ

where γ is the Mn–O–Mn angle and dMn–O is the Mn–O bondlength. The calculated values of W for samples are presented inTable 1. It is found that the bandwidth increases with increasinggrain size. The increase in bandwidth increases the overlapbetween the Mn-3d and O-2p orbitals, which results in theincrease in TC.

In order to gain further insight into the nature of superpar-amagnetic behavior in samples, we investigated the room tem-perature magnetic hysteresis curves for samples. The results aredisplayed in Fig. 4. From this figure we can observe that themagnetization increases with increasing applied field, whichresults from the progressive alignment of an ensemble of magneticparticles. However, the magnetization is not saturated up to a fieldof 3 kOe. Because the curves clearly indicate zero remanence and

100 nm 100 nm

100 nm

Fig. 2. FE-SEM picture of S1 (a), S2 (b) and S3 (c) samples.

D.H. Manh et al. / Physica B 444 (2014) 94–10296

0

2

4

6

8

10

12

0 100 200 300 400

M (e

mu/

g)

T (K)

6789

101112

0 90 180 270 360

M (e

mu/

g)

TB

T (K)

FC

ZFC

0

2

4

6

8

10

0 100 200 300 400T (K)

M (e

mu/

g)

6789

1011

0 100 200 300 400T (K)

M (e

mu/

g)

TB

0

2

4

6

8

10

0 100 200 300 400T (K)

FC

ZFC

56789

0 70 140 210 280 350T (K)

M (e

mu/

g)

TB

M (e

mu/

g)

Fig. 3. The temperature dependence of the magnetization measured under a magnetic field of 100 Oe in the ZFC and FC modes for (a) S1, (b) S2 and (c) S3. Blocking at TB isshown by arrows in the inset.

-40

-20

0

20

40

-3 -2 -1 0 1 2 3

S1

M (e

mu/

g)

H (kOe)

T = 300 K

-54

-27

0

27

54

-3 -2 -1 0 1 2 3

S3

M (e

mu/

g)

H (kOe)

T = 300 K

-50

-25

0

25

50

-3 -2 -1 0 1 2 3

S2

M (e

mu/

g)

H (kOe)

T = 300 K

Fig. 4. Room-temperature magnetization data for S1 (a), S2 (b) and S3 (c) samples. The solid line shows the fit to Langevin theory.

D.H. Manh et al. / Physica B 444 (2014) 94–102 97

coercivity, it is deduced that all the samples exhibit superpara-magnetic behavior. In order to understand the superparamagneticnature of a M–H curve at 300 K, magnetization data are analyzedunder the framework of Langevin's theory [31]. According to thistheory, in superparamagnetic regime, the temperature and fielddependences of magnetization of an assemble of N noninteractingidentical particles with the magnetic moment μef can be describedby Langevin function [31]

M¼Nμef cthμefHkBT

� �� kBTμefH

� �ð5Þ

Eq. (5) fits the data very well at 300 K. The plots and fittingresults depicted in Fig. 4 reveal that the magnetic field depen-dences of the magnetization at 300 K show a typical characteristicof superparamagnetic systems. As mentioned above, the blockingof magnetic particle, represented by a cusp, at the blockingtemperature TB¼Tmax, in the MZFC(T) plot, is related to its magneticanisotropy. The relationship between the blocking temperature(TB) and the effective anisotropy constant (Keff) is expressed byequation:

KeffV ¼ 25kBTB ð6Þ

Taking TB obtained from MZFC(T) measurement (see Table 1)and by using Eq. (6), effective anisotropy constant of Keff isobtained to be 2.18�105, 0.66�105 and 0.15�105 erg/cm3 forS1, S2 and S3, respectively. The value of Keff for the particles of21 nm diameter was found to be 2.24�104 erg/cm3 [32]. However,the value obtained in our study is one order of magnitude higherthan in the similar sample. This may be due to increasing internalstrain with decreasing particle size. In article published by Muthu-selvam and Bhowmik [33], the similar TB were observed in nanoLa0.67Sr0.33MnO3 having grain size from 72 nm to 86 nm. More-over, a recent article by Thorat et al. [12] has reported thesuperparamagnetic nature at room temperature and the blocking

temperature for the two different samples of La0.7Sr0.3MnO3

nanoparticles (40 nm and 60 nm).Fig. 5 presents the magnetization as a function of the applied

field at various temperatures. In order to understand the nature offield dependence of magnetization, the magnetic curves of theLSMO nanoparticles at different temperatures were analyzed usingthe law of approach to saturation, which is expressed as [34]

MðHÞ ¼MsaH� b

H2�…� �

þχdH ð7Þ

where Ms and χd are the saturation magnetization at a particulartemperature and the high field susceptibility, respectively. Theb/H2 term has its origin in the various kinds of magnetic aniso-tropies such as magnetocrystalline anisotropy, surface anisotropy,shape anisotropy and strain anisotropy.

Assume that the particles are oriented randomly and that thestrain distribution is homogeneous for the LSMO nanoparticle,it can be denoted that [35–36]

b¼ 1

M2s

8105

K21þ

415

K2shþ

35λ2s2

� �ð8Þ

where K1 and Ksh are the magnetocrystalline anisotropy constantand the shape anisotropy constant, respectively, λ¼ jλsj is thesaturation magnetostriction constant and s is the strain.

An effective anisotropy constant Keff for discussion is defined asfollows [36]:

K2eff ¼ K2

shþ94λ2s2 ð9Þ

Hence b is expressed by

b¼ 1

M2s

8105

K21þ

415

K2eff

� �ð10Þ

From the magnetization curves near the saturation region,b may be deduced. Using Keff obtained from Eq. (6), K1 may becalculated from the above expression. The values of K1 are found to

40

50

60

70

80

0 10 20 30 40 50

H (kOe)

M (e

mu/

g)

10 K

300 K55

60

65

70

75

80

85

0 10 20 30 40 50

M (e

mu/

g)

H (kOe)

10 K

300 K

55

60

65

70

75

80

85

90

0 10 20 30 40 50H (kOe)

M (e

mu/

g)

10 K

300 K

Fig. 5. Field dependence of magnetization measured at several temperatures from 10 K to 300 K for S1 (a), S2 (b) and S3 (c). The solid lines show the fitting of themagnetization curves of samples using Eq. (7) described in the text.

D.H. Manh et al. / Physica B 444 (2014) 94–10298

be 4.59�105, 3.66�105 and 0.54�105 erg/cm3 at 300 K for S1, S2and S3, respectively. These values are higher than those of similarsingle crystals manganites, K1¼1.8�104 erg/cm3 at 300 K [37] andare found to decrease with an increase in particle size. We nowfocus our attention on the M–H curves in these samples. For allsamples magnetization is unsaturated up to a field of 5 kOe. It isobserved that Ms increases with sintering temperature and max-imum value of Ms is 86.67 emu/g for S3 at 10 K, much lower thanthe theoretical value Ms¼103 emu/g and the experimentallyestimated value for the bulk [38]. On the other hand, as thetemperature increases, the saturation magnetization of LSMOmaterials decreases (Fig. 6). The temperature dependence ofsaturation magnetization Ms arises due to the spin wave fluctua-tions described by the following equation [39]:

Ms ¼Msð0Þð1�BTεÞ ð11Þwhere Ms(0) is the saturation magnetization at T¼0 K and B is theBloch constant, which is closely related to the exchange integral,J (B�1/Jε). Eq. (11) is known as the Bloch T3/2 law for ε¼3/2 [40],which has been confirmed experimentally for most of the bulkmaterials; however, for nanostructured materials, Mills and Mar-adudin [41] reported value ε¼3/2, similarly in case of bulkmaterials. Theoretical work of Hendriksen et al. [42] has shownthat the Bloch exponent ε should increase as the particle sizereduces. A large number of other studies have been performed inthe ultrafine magnetic particles. Results show that the deviationfrom T3/2 in those systems is due to the finite size effects such asan energy gap in the density of states of spin-waves and lack ofmagnetic coordination at the surfaces [43]. The best fits to Eq. (11)yield the value ε¼1.59, 1.58 and 1.55 for the samples S1, S2 and S3,respectively.

The effective magnetic anisotropy constants Keff, the magneto-crystalline anisotropy constants K1, the saturation magnetization

values at zero temperature Ms(0) and the Bloch exponent ε forsamples S1, S2 and S3 are presented in Table 2.

In order to study the AC magnetic heating characteristic ofthese nanoparticles, the dependence of the heat generation onaltering the applied magnetic fields of the three samples wasmeasured at a fixed frequency of 236 kHz and under differentmagnetic field amplitudes from 50 to 80 Oe. The experimentswere performed for 25 min with sample concentration of 15 mg/mL in distilled water for each sample. The results for temperaturerise are shown in Fig. 7. It is observed that these heating curvesclearly manifested that after a period of time of about 15 min(1000 s) the ferrofluid temperature tends to saturate at somecharacteristic temperature Ts, as detailed in Table 3. The initialrise in temperature with time of single domain LSMO nanoparti-cles in an external AC magnetic field can be attributed to two kindsof loss processes: hysteresis loss and relaxation losses (i.e. Neellosses and Brownian losses) [44]. For single domain systemswithout superparamagnetic characteristic, depending on theirsize, the SAR can be caused by both loss processes [45]. However,because in our case LSMO MNPs show superparamagnetic beha-vior at temperature, the total amount of heat generation is onlydue to contribution of relaxation processes. The Specific Absorp-tion Rate for the nanoparticles can be determined using thefollowing expression [46]:

SAR¼∑i

Cimi

mdTdt

ð12Þ

where Ci is the specific heat capacity of the ith component inferrofluid, mi is the mass of component (LSMO nanoparticles andwater), m is the mass of the LSMO in ferrofluid and dT/dt is theinitial slope of the time dependence of a temperature curve. Inthese experimental parameters, we use the linear relations inranges 0–5 min intervals in order to calculate dT/dt. Calculations

30

40

50

60

70

80

0 50 100 150 200 250 300 350

Ms

Ms (e

mu/

g)

T (K)

40

50

60

70

80

90

100

0 50 100 150 200 250 300 350

Ms

Ms (

emu/

g)

T (K)

50

60

70

80

90

100

0 50 100 150 200 250 300 350

Ms

Ms (

emu/

g)

T (K)

Fig. 6. Temperature dependence of saturaton magnetization (Ms) of S1 (a), S2 (b) and S3 (c). The solid lines show the fit curves according to the modifield Bloch law(Eq. (11)).

D.H. Manh et al. / Physica B 444 (2014) 94–102 99

were based on specific heat capacities of 0.66 [47] and4.18 J g�1 K�1 for LSMO and water, respectively. The SAR valuesobtained are indicated in Table 3 and it can be seen that the SARincreases with increasing particle size. This result is consistentwith that of single domain La0.75Sr0.25MnO3 systems [48]. Thephysical basis of the heating of superparamagnetic LSMO nano-particles by AC magnetic fields has been briefly explained in somerecent publications [5,48,49]. The magnetic fluid hyperthermiastudy of Thorat et al. [49] clearly shows surface functionality-dependent SAR values in oleic acid–betaine HCl-coated La0.7Sr0.3MnO3

systems. Further, they believed that these surface functionalizedLSMO nanoparticles can be used as an excellent heating source formagnetic fluid hyperthermia.

It is well known that in ferrofluids the power loss correspond-ing to Neel or Brown relaxation for superparamagnetic nanopar-ticles is approximately given by [21]

P ¼ ðmHωτÞ2=½2τkBTρVð1þω2τ2Þ� ð13Þ

where m is the particle magnetic moment, τ is the magneticrelaxation time, ω the measurement angular frequency, H the ACfield intensity amplitude and ρ the density of LSMO nanoparticles.The power loss will reach the maximum when ωτ¼1. The Neelrelaxation time is

τN ¼ τ0expðKV=kBTÞ ð14Þ

and the relaxation time of Brownian motion is

τB ¼ 4πηr3=kBT ð15Þwhere τ0 is the time constant (�10�9 s), K is magnetocrystallineanisotropy constant, V is the particle volume, kB is Boltzmann'sconstant, η is viscosity of carrier liquid, and r is the hydrodynamicradius of the particle. Hiergeist et al. [50] reported that in the caseof relaxational losses in superparamagnetic ferrofluids, theorypredicts a square or a linear law depending on the ratio of externalfield frequency to the characteristic relaxation frequency of theparticle system. However, in our case, an H2-law was observed forthe dependence of SAR on the amplitude of the AC magnetic field(Fig. 8). This proves that a type of superparamagnetic and singledomain behavior exists in ferrofluids, which is consistent with theabove discussions.

In a recent report, Kallumadil et al. [17] suggested a newparameter “intrinsic loss power” (ILP) in order to directly comparethe SAR reported in the literature with that of other ferrofluidsunder different AC field strengths and frequencies. The ILP wasdefined as

ILP¼ P

ρH2f¼ SAR

H2fð16Þ

The ILP was calculated from Eq. (16) to be 2.67, 3.09 and4.07 nHm2/kg for samples S1, S2 and S3, respectively. These arecomparable to those of a series of La1�xSrxMnO3 nanoparticles

Table 2Magnetization parameters of La0.7Sr0.3MnO3 nanoparticles.

Sample TB (K) TC (K) Ms (emu/g) at 0 K B�10�5 (K�ε) ε Keff�105(erg cm�3) K1�105(erg cm�3)

S1 265 346 80.13 5.47 1.59 2.18 4.59S2 270 356 89.85 4.90 1.58 0.66 3.66S3 277 360 91.69 4.86 1.55 0.15 0.54

30

40

50

60

70

8050 Oe60 Oe70 Oe80 Oe

T (o C

)

t (s)

30

40

50

60

70

8050 Oe60 Oe70 Oe80 Oe

T (o C

)t (s)

30

40

50

60

70

80

90

0 200 400 600 800 1000 1200 1400 1600 0 200 400 600 800 1000 1200 1400 1600

0 200 400 600 800 1000 1200 1400 1600

50 Oe60 Oe70 Oe80 Oe

t (s)

T (o C

)

Fig. 7. Heating curves of LSMO ferrofluid at different values of AC magnetic field amplitudes for S1 (a), S2 (b) and S3 (c).

D.H. Manh et al. / Physica B 444 (2014) 94–102100

(0.15rxr0.45) reported by Rashid et al. [5]. The comparison ofthe ILP of some commercial ferrofluids with different hydrody-namic sizes was shown in Ref. [17]. The highest ILPs of 3.12 and3.1 nHm2/kg in commercial ferrofluids have hydrodynamic sizes of91 and 61 nm and particle sizes of 11.8 and 10.5 nm, respectivelybelonging to Micromode and Bayer–Schering ferrofluids. Compar-ing our results with the results in that report shows that the ILP ofsample S3 is higher than all the commercial ferrofluids. Thissuggests potential for use in magnetic hyperthermia.

4. Conclusions

In summary, the structural, the magnetic and the heatingbehaviors of La0.7Sr0.3MnO3 nanoparticles have been studied.La0.7Sr0.3MnO3 has the hexagonal structure and diameter increasesfrom 20 to 50 nm; its unit volume and bond angle increase whileits bond length decreases. The effective magnetic anisotropy andthe magnetocrystalline anisotropy constant decrease with increas-ing particle diameters. This may be due to the decreased internalstrain with increasing particle size. The investigation on the heatgeneration of La0.7Sr0.3MnO3 nanoparticles indicated that theSpecific Absorption Rate was dependent on the amplitude of ACmagnetic field and particle size. The highest value of SpecificAbsorption Rate is 36.87 W/g for the 50 nm sample, correspondingto intrinsic loss power of 4.07 nHm2/kg. Furthermore, the SARvalue can be finely adjusted according to the surrounding medium.Thus, La0.7Sr0.3MnO3 nanoparticles can be a promising candidatefor the magnetic hyperthermia as well as other biomedicalapplications.

Acknowledgments

This study was supported by Vietnam National Foundation forScience and Technology Development (NAFOSTED) under Grantnumber 103.02-2011.31 and the Dongguk University-GyeongjuFund of 2013.

References

[1] K.L. Ang, S. Venkatraman, R.V. Ramanujan, Mater. Sci. Eng. C 27 (2007) 347.[2] L.A. Harris (Ph.D. Thesis), Virginia Polytechnic Institute and State University,

2002.[3] V. Salgueirino-Maceira, M.A. Correa-Duarte, M. Farle, M.A. Lopez-Quintela,

K. Sieradzki, R. Diaz, Langmuir 22 (2006) 1455.[4] Nhiem Tran, T.J. Webster, J. Mater. Chem. 20 (2010) 8760.[5] Amin ur Rashid, Ashfaq Ahmed, S.N. Ahmad, S.A. Shaheen, Sadia Manzoor,

J. Magn. Magn. Mater. 347 (2013) 39.[6] K.M. Krishnan, A.B. Pakhomov, Y. Bao, P. Blomqvist, Y. Chun, M. Gonzales,

K. Griffin, X. Ji, B.K. Roberts, J. Mater. Sci. 41 (2006) 793.[7] Y. Bao, M. Beerman, A.B. Pakhomov, K.M. Krishnan, J. Phys. Chem. B 109 (2005)

7220.[8] S. Sun, Adv. Mater. 18 (2006) 393.[9] A.P. Khandhar, R.M. Ferguson, J.A. Simon, K.M. Krishnan, J. Biomed. Mater. Res.

Part A 100 (2012) 728.[10] O. Kaman, E. Pollert, P. Veverka, M. Veverka, E. Hadová, K. Knižek, M. Maryšk,

P. Kašpar, M. Klementov, V. Grunwaldov, S. Vasseur, R. Epherre, S. Mornet,G. Goglio, E. Duguet, Nanotechnology 20 (2009) 275610.

[11] N.K. Prasad, K. Rathinasamy, D. Panda, D. Bahadur, J. Biomed. Mater. Res. Part B85 (2007) 409.

[12] N.D. Thorat, K.P. Shinde, S.H. Pawar, K.C. Barick, C.A. Betty, R.S. Ningthoujam,Dalton Trans. 41 (2012) 3060.

[13] Y.H. Huang, C.H. Yan, S. Wang, F. Luo, Z.M. Wang, C.S. Liao, G.X. Xu, J. Mater.Chem. 11 (2001) 3296.

[14] Y.W. Duan, X.L. Kou, J.G. Li, Physica B 355 (2005) 250.[15] R. Epherre, E. Duguet, S. Mornet, E. Pollert, S. Louguet, S. Lecommandoux,

C. Schatzcd, G. Goglio, J. Mater. Chem. 21 (2011) 4393.[16] D.H. Manh, P.T. Phong, T.D. Thanh, D.N.H. Nam, L.V. Hong, N.X. Phuc, J. Alloys

Compd. 509 (2011) 1373.[17] M. Kallumadil, M. Tada, T. Nakagawa, M. Abe, P. Southern, Q.A. Pankhurst,

J. Magn. Magn. Mater. 321 (2009) 1509.[18] D.H. Manh, T.D. Thanh, N.X. Phuc, L.V. Hong, P.T. Phong, L.T. Hung, Int.

J. Nanotechnol. 8 (2011) 241.[19] H.M. Rietveld, J. Appl. Crystallogr. 2 (1969) 65.[20] T.T. Luong, T.P. Ha, L.D. Tran, M.H. Do, T.T. Mai, N.H. Pham, H.B.T. Phan, G.H.

T. Pham, N.M.T. Hoang, Q.T. Nguyen, P.X. Nguyen, Colloids Surf. A: Physico-chem. Eng. Asp. 384 (2011) 23.

[21] B. Behdadfar, A. Kermanpur, H. Sadeghi-Aliabadi, M.P. Morales, M. Mozaffari,J. Solid State Chem. 187 (2012) 20.

[22] R. Bindu, Eur. Phys. J. B 37 (2004) 321.[23] B.D. Cullity, Elements of X-ray Diffraction, 2nd ed., Addison-Wesley, Reading,

MA (1978) 356.[24] S. Mørup, M.F. Hansen, C. Frandsen, Magnetic Nanoparticles, Elsevier B.V.

(2011) 437.[25] R.D. Sanchez, J. Rivas, D. Caeiro, M. Ostlund, M. Servin, C. Vazquez, M.A. Lopez-

Quintela, M.T. Causa, S.B. Oseroff, Mater. Sci. Forum 831 (1997) 235.[26] P. Dey, T.K. Nath, Appl. Phys. Lett. 89 (2006) 163102.[27] D.N.H. Nam, L.V. Bau, N.V. Khiem, N.V. Dai, L.V. Hong, N.X. Phuc, R.S. Newrock,

P. Nordblad, Phys. Rev. B 73 (2006) 184430.[28] W.J. Lu, X. Luo, C.Y. Hao, W.H. Song, Y.P. Sun, J. Appl. Phys. 104 (2008) 113908.[29] R.D. Sánchez, J. Rivas, C. Vázquez-Vázquez, A. López-Quintela, M.T. Causa,

M. Tovar, S. Oseroff, Appl. Phys. Lett. 68 (1996) 134.[30] M.S. Kim, J.B. Yang, Q. Cai, X.D. Zhou, W.J. James, W.B. Yelon, P.E. Parris,

D. Buddhikot, S.K. Malik, Phys. Rev. B 71 (2005) 014433.[31] B.D. Cullity, Introduction to Magnetic Materials, Addison-Wesley, London,

1972.[32] A. Rostamnejadi, H. Salamati, P. Kameli, H. Ahmadvand, J. Magn. Magn. Mater.

321 (2009) 3126.[33] I. Panneer Muthuselvam, R.N. Bhowmik, J. Alloys Compd. 511 (2012) 22.[34] A.H. Morrish, The Physical Principles of Magnetism, Wiley, New York, 1965.[35] K. Ho, X. Xiong, J. Zhi, L. Cheng, J. Appl. Phys. 74 (1993) 6788.[36] H. Yang, Z. Wang, L. Song, M. Zhao, J. Wang, H. Luo, J. Phys. D: Appl. Phys. 29

(1996) 2574.[37] Y. Suzuki, H.Y. Hwang, S.-W. Cheong, T. Siegrist, R.B. van Dover, A. Asamitsu,

Y. Tokura, J. Appl. Phys. 83 (1998) 7064.[38] N.X. Phuc, Ha M. Nguyen, D.H. Manh, L.T. Hung, L.T.C. Tuong, L.V. Hong, Yeong-

Der Yao, J. Magn. Magn. Mater. 304 (2006) 133.[39] A.E. Berkowitz, W.J. Shuele, P.J. Flanders, J. Appl. Phys. 39 (1968) 1261.[40] M. Thakur, K. De, S. Giri, S. Si, A. Kotal, T.K. Mandal, J. Phys.: Condens. Matter 18

(2006) 9093.[41] D.L. Mills, A.A. Maradudin, J. Phys. Chem. Solids 28 (1967) 1855.[42] P.V. Hendriksen, S. Linderoth, P.A. Lindgård, Phys. Rev. B 48 (1993) 7259.[43] Nguyen Thi Lan, Nguyen Phuc Duong, Than Duc Hien, J. Alloys Compd. 509

(2011) 5919.

Table 3Saturation temperature Ts, dT/dt, SAR and ILP of La0.7Sr0.3MnO3 ferrofluid atdifferent values of magnetic field aplitude (H).

H(Oe)

Sample S1 Sample S2 Sample S3

Ts(1C)

dT/dt(1C/s)

SAR(W/g)

Ts(1C)

dT/dt(1C/s)

SAR(W/g)

Ts(1C)

dT/dt(1C/s)

SAR(W/g)

50 49 0.036 10.06 55 0.039 10.89 57 0.069 19.2760 51 0.049 13.69 61 0.062 17.32 63 0.086 24.0270 59 0.070 19.55 67 0.084 23.46 65 0.101 28.2180 67 0.095 26.54 70 0.103 28.77 76 0.128 35.75

0

10

20

30

40

0 10 20 30 40 50

S1S2S3

H 2 (kA/m)2

SAR

(W/g

)

Fig. 8. Experimental data of SAR in dependence on the square of the AC magneticfield amplitude for a ferrofluid sample and according fit.

D.H. Manh et al. / Physica B 444 (2014) 94–102 101

[44] R. Hergt, S. Dutz, R. Muller, M. Zeisberger, J. Phys.: Condens. Matter 18 (2006)S2919.

[45] A. Doaga, A.M. Cojocariu, W. Amin, F. Heib, P. Bender, R. Hempelmann,O.F. Caltun, Mater. Chem. Phys. 143 (2013) 305.

[46] R.A. Frimpong, J. Dou, M. Pechan, J. Zach Hilt, J. Magn. Magn. Mater. 322 (2010) 326.[47] D. Kim, B.L. Zink, F. Hellman, J.M.D. Coey, Phys. Rev. B 65 (1994) 214424.

[48] S. Vasseur, E. Duguet, J. Portier, G. Goglio, S. Mornet, E. Hadová, K. Knižek,M. Maryško, P. Veverka, E. Pollert, J. Magn. Magn. Mater. 302 (2006) 315.

[49] N.D. Thorat, R.M. Patil, V.M. Khot, A.B. Salunkhe, A.I. Prasad, K.C. Barick,R.S. Ningthoujam, S.H. Pawar, New J. Chem. 37 (2013) 2733.

[50] R. Hiergeist, W. Andra, N. Buske, R. Hergt, U. Richter, W. Kaiser, J. Magn. Magn.Mater. 201 (1999) 420.

D.H. Manh et al. / Physica B 444 (2014) 94–102102