NUCLEARNuclearPhysicsB 374 (1992)263—276 P H V S I CS BNorth-Holland

Boundson lB from latticeQCD *

C. Alexandroua s. Güskenb F. Jegerlehnera K. Schilling b andR. Sommer

PSI, CH-5232Villigen, Switzerlandb PhysicsDepartment,Universityof Wuppertal,D-5600 Wuppertal1, Germany

CERN,TheoryDivision, (‘P1-1211 Geneva23, Switzerland

Received17 June1991(Revised18 December1991)

Acceptedfor publication18 December1991

We presenta study of finite-a effectsin theleptonicdecayconstantf~,of heavypseudoscalarmesons.Exploiting resultson threelattices — with inverse lattice spacingsa — = 3.35, 2.3 and1.53 GeV — to extrapolatef~,to a = 0, we can boundtheB-mesondecayconstantfB. within thequenchedapproximation,by 188 MeV < f~<246 MeV. This range of fB allows for sizeable(‘P-violationeffectsin theB-mesondecayBJ(Bd)—~J/i~i K~.

1. Introduction

Weakdecaysof heavyhadronsplay a key role in probing the hadronicsectorofthe successfulStandardModel of electroweakinteractionswith the threequark—lepton family scenario(see e.g. ref. [1]). The big challengeis to establishdirect

CP-violation effects in B-decays, as they are predicted in the Cabibbo—Kobayashi—Maskawa(CKM) mechanism[2—41.Within this scheme,by virtue ofthe unitarity of the CKM matrix, the CP-violation effects, in principle, can bepredicted entirely in terms of CP-conservingexperimentalquantities.At presentthe most importantconstraintsfor the CP-violatingCKM phase5 comefrom theobservedCP violation in the K°—K°systemand from the ARGUS and CLEOresultson B°—B°mixing andsemileptonicB-decays[5—71.A predictionof S is not

possible, though,becausewe are still lacking experimentalknowledgeof the topmass m~,the leptonic B-mesondecayconstantfB and the BB factor. Moreover,the determinationof CKJvI matrix elementsis hamperedby our rather limitedability to predicthadronicmatrix elements(decayconstants,B-factors andother

form factors).Theoretical predictions are particularly difficult for heavy—light bound states

like the D- and B-mesons.Thereforeprevioustheoreticalestimatesfor fB differ

* Work supportedin part by DeutscheForschungsgemeinschaftgrantSchi 257/1-2.

0550-3213/92/$05.00© 1992 — ElsevierSciencePublishersBy. All rights reserved

264 C. Alexandrouet al. / Boundson fB

widely. They are basedon QCD sum rules [8,91,lattice calculationsand various

potentialmodels(see e.g. ref. [101).For large massm~the scalinglaw [11]

fp(m~)~~= const.

is expectedto be valid. A value fB 110 MeV is then obtainedby extrapolatingwith the scalinglaw from thevalue for fD 180 MeV which comesout from bothQCD sumrules [8,9] andlattice calculations[12—14].Usually a range 100 MeV ~

fB ~ 200 MeV has beenanticipatedin phenomenologicaldiscussions[3,4,7].Val-uesfor fB in the lower part of this rangewould imply rather pessimisticprospectsfor CP-violationexperiments,evenat B-factorieswith luminosity ashigh as i0~cm2 sec~(see e.g. ref. [3]).

Morerecentdevelopmentsin lattice simulations,basedon a static treatmentofthe heavyb-quark [15], led to lattice estimatesfor fB which areby a factor two tothree higher than the quoted conventionalvalues[13,16,17].We should mentionthat large valuesfor fB havebeen obtainedin the QCD sum rule and in thepotential model approachesas well [8,10]. In ref. [18] large valuesfor fB 250MeV andsin S ‘~ 0.89 were found as a resultof a “global fit” to presentdata~. It

has been pointed out recently [19] that a value fB in the range 200—300 MeVwould drasticallychangethe outlook of the proposedCP-violation experiments.For example, CP-violating asymmetriesin the pilot reaction Bd(Bd) —‘ J/~K~could be enhancedby an order of magnitudein rate and could thus safelybemeasuredat storagerings with technicallyachievableluminosities.

Needlessto say,a full lattice determinationof fB, beingan ab initio calculationfrom the QCD lagrangian,would be superiorto any otherway of predictingthisquantitywhich is so badly needed.A numberof pioneeringlattice simulationshavebeencarriedout previously to studybeauty- physics in the quenchedapproxima-tion [12—14,17].

Practical lattice simulationsof QCD are faced, however,with a number ofproblemsthat must be carefully dealtwith before one can claim reliable resultsfrom this theoreticalapproach.For B-mesons,dueto their large mass,the limitedlattice resolution (finite lattice constant a) is potentially the most dangeroussourceof a systematicerror: with quarkstreated as Wilson fermions, as we dothroughoutthis paper, such scaling violations are first-order effects in a. In theinstanceof heavy—light quark systemson the lattice, 0(a) terms translateinto0(M

1) effects, since massesM1, given in lattice units, are related to the physicalmassesm, by M1 = am1.Therefore,with presentlattice resolutionlimited to latticespacingsa ~(4 GeVY’, we haveto copewith the problemthat MB> 1!

* The result of this analysiscrucially dependson the value e ‘/e = (2.0±1.8)x i0~ used as a

constraint.This value is controversial,however.

C. Alexandrouetat / Boundson f~ 265

In the following we will presentnew results for fB’ obtainedon a 18~x 48lattice at /3 = 6.26, which correspondsto a lattice spacing a = (3.35 GeVY1. Wewill combine them with our previous high-precision data, obtained at inverselattice spacingsa~’= 1.53 and 2.3 GeV [13]. An elaborateanalysis of the wholedataset will enableusto estimatethe continuumvaluefor fB, via extrapolationtolattice spacinga = 0. As a result, we will end up with a fairly coherentpicture,

wherethe estimatefor thepseudoscalardecayconstantin thestatic approximation[161 can be reached by extrapolation from the standard,non-static results aspresentedhere.Moreover,we can boundthe leptonic B-mesondecayconstanttothe range 188 MeV <fB <246 MeV. We shall discuss the phenomenologicalimplicationsof this result in sect.3.

2. The lattice calculation of lB

Definitions. In this section, we will briefly define the quantitiesused in ourpresentanalysis ~. The computationof the pseudoscalardecayconstantstartsfrom

the correlationfunctions

C11(T) = E <O~(X,T)(01(O,0))5, i, j = P, A (1)

of the operators

OA(X, T) =h(X, T)70y51(X,T), O~(X,T) =h(X, T)-y51(X,T). (2)

Throughoutthis section,capital letterswill be usedfor quantitiesin lattice units,and the correspondinglower caseletters designatethe samequantitiesin physicalunits. For sufficiently largetime T, the correlationfunctions(1) aredominatedbythe lowest pseudoscalarstate I P )‘, with normalisationK P I P) = 1,

Cjj(T)~(K0IOj(0)IP>(PIOj(0)tI0)exp(_MpT))±(T~*LT_T). (3)

The decayconstantF~,usinga normalisationwheref~= 132 MeV, is given by **

ZA(0IOA(0)IP~=FP(m,, mh)/MP(m/, mh)/

2 (4)

with ZA being the perturbativerenormalisationconstantof the axial vectorcurrent[21] and m, (mh) the light (heavy)quarkmass.

* For any details of the simulation we refer the readerto ref. [13] and a forthcoming longer

publication on our resultsfor heavy—light mesons[20].** Note that in ref. [13] a form hasbeenused that assumesthat the pseudoscalarstateis described

effectively as a lattice bosonwith nearestneighbourkinetic energy.We do not do this here, sincelattice artifactsare treatedexplicitly.

266 C. Alexandrouet al. / Boundson fB

Finite-a effects. In order to convert F~into physical units, we determinethelattice constantap by matchingto the p-mesonmass:a~m~= A1~.In this context,

we preferthe p-massto any otherphysical observable,sinceit canbe determinedmost precisely in a lattice calculation. In particular, it allows for a smoothextrapolationto thephysical light quarkmass.Of course,any otherchoice,like theproton mass, for example,would be as legitimate.Apart from effectsdue to thequenchedapproximation,this would only changethe sizeof the scalingviolations.With the presentchoice of a, the decayconstantf~is given by

ç’F~(m~, mh) =f~(m1,mh)[1+O(aP)1, (5)

a form suggestedby a perturbativeanalysis(for a brief discussionin the contextofan improved fermion action see ref. [22]). Since the scaling violations in thisexpressionare actually found to be rather small (seeref. [131as well as fig. 1), weattemptto describethemby the simpleansatz

a~1F~(m,,m

6) =fp(mp(m,, mh))[1 +ba~j[1 +dMp(m~,mh)]. (6)

This form is suggestedby the simulationdata: the first correctionis motivated bythe observationthat finite-a effectsappearto be still sizeableevenat small quarkmasses.The secondcorrectionfactor accountsfor the expectedgrowth of latticeartifacts with increasingmassof the pseudoscalarstate M~.For fixed m~,thissecondterm inducesa finite-a correction,which dominatesthe overall first-ordercorrection (and thus constitutesthe full correctionterm of eq. (5)), in the casewhere all masses(in lattice units) of hadronsmadeout of “light” quarksonly arewell below 1! In thefollowing we will makeuseof eq.(6) asour phenomenologicalparametrizationof the lattice artifacts.

Mass dependence.Next, we need to parametrizethe me-dependenceof thedecayconstantat fixed light quarkmass.This is doneby the following ansatz:

a (e2”3mB) 6/25 N

f~(m~)= m~”~~ c,,m~’1, (7)a~(e- . mp) n=O

which is motivatedby the 1/me expansionaround the static (m~—~ oc) limit [161.At a light quarkmass,fixed by m~(m,,mo = a~’M~(m

0,m0) = 1.05GeV, ourfit (on a total of 20 datapoints, at 3 different valuesof the inverselattice spacing,

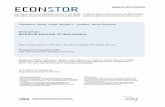
= 1.53 GeV, 2.30 GeV, 3.35 GeV) rendersa = 10.0. This signalsa reason-able fit, consideringthe fact that the datapoints within each of the 3 sets arecorrelated.Indeed,fig. I shows that we havefound an adequateeffective descrip-tion of the data that will serve as the basis for our prediction of the leptonicB-mesondecayconstant.

C. Alexandrouetal. / Boundson fB 267

0.320

c~’0.28

,~k

::~.0.16

0.12

0.08

o ~ = 1.53 GeV0.04

° o~ = 2.30 GeV

~ ~ — 3.35 GeV0 I I I I

0. 0.2 0.4 0.6 0.8 1. 1.2

o~M~~*GeV

Fig. 1. a/1Fp(m,.,mh) as a function of m~= a~M~’.The fit describedin the text is given by the

dashedline (a~ = 3.35 GeV), the dash—dottedline (at’ = 2.3 GeV) and the dotted line (a/1 = 1.53GeV).Thesolid curverepresentsthe extrapolationto a = 0.

The best fit parameters,with N = 3 preset, are b = 0.532, d = — 0.129 andc0, c1, c2, c3 = 0.716(65), —1.04, 0.83, —0.28measuredin powersof GeV. In view

of the fact that we applyeq.(7) in the range0.18GeV~<m~’<1.2 GeV1, the

sizeof the coefficientsc,, suggestssufficientconvergenceof eq. (7).Sincethe fit parametersare stronglycorrelated,we quote theerrorsonly for the

interesting leading term C

0 and the overall functions f~(m~).The statisticaluncertaintyof the latter varies from 8 MeV at m~= 3 GeV to 10 MeV at theB-mesonmass.We shouldmentionthat both c1 and c2 are significantly differentfrom zero,which impliesviolation of massscalingf~/~= const.evenbeyondtheB-mesonmassrange.Violation of this scalinglaw hasbeenobtainedpreviously ina versionof the QCD sumrule approach[91as well.

268 C. Alexandrouet a!. / Boundson f8

Consistency checks. It is tempting to makea consistencycheck,in order to testwhethereq.(7) remainsa valid descriptionin the massrangebeyondthe B-mesonmass:the questionis whetherc0 coincideswith the static result

f~tat~fp~/(as(e2/3mp)/aS(e21/3mB))6~’2S,

that canbe computedindependently,in the static limit [16]. In ref. [131,we have

determined fstat = 1.4 GeV3~2at a~= (1.53 GeV)~and fstat = 1.1 GeV3”2 ata~= (2.3 GeV)~.Thesevalues decreasefurther to foal = 0.94 GeV3~2at a~=

(3.35 GeV)~.The statisticaluncertaintyon thesenumbersis small (about 5%),while the systematicerror,dueto the perturbativerenormalisationof this quantity,

may be as large as 20%. It is reassuringto seef~t~~tapproachc0! In fact, despite

the large size of scalingviolations in fSt~I thesevaluesfollow surprisinglywell alinear behaviourin a, giving f~= 0.57 GeV

3”2 at a = 0. Within the systematic

uncertaintyof f~t~tthis valueis in agreementwith c0 = 0.716(65)!

The fitted f~(m~)and c0 turn out to be quite stablewith respectto variantsof

eq. (7), like modifying N to 2 or 4 or switchingfrom polynomial to Fadeforms.We mention another check on the systematicsof our treatment of lattice

artifacts:for mesonscomposedof two light quarks,the secondquarebracket in eq.(6) is negligible. We can thereforeusethe experimentalvaluesof fK’ f~7.andeq.(6) to approximately“predict” the expected lattice numbers(that include the

finite-a effects),for both FK and F.,,.. Thesenumbersagreewith our direct MonteCarlo results as well as with the onesof the APE group [23] within the 10%statisticalerrors. In otherwords,onewould obtain compatible resultsif the scalewere introducedinto eq. (5) through fK ratherthan through mp ~. In order tofurther substantiateour results, we haverepeatedthe above fitting procedures,after replacinga~by a,,., the latter being definedas the lattice spacingobtainedfrom matching to the string tension. Doing so, we arrive at compatible results,

thoughwithin largeroveralluncertainties,which are characteristicof stringtensionmeasurements[24].

At the B-mesonmass,our fit yields f~(m~= 5.28 GeV) = 239(10) MeV, whichis only a mild extrapolationwith respectto thelast datapoint. In the following weshall use, in addition to the statisticalerror, half of the difference betweenthelatter two values,namely8 MeV, as our estimateof thesystematicerror dueto thephenomenologicalansatzfor treating lattice artifacts. This difference is smallbecauseb and d haveoppositesigns, which leadsto a partial compensationoffinite-a effects.

Thereis anotherway to look at the problem,which will help usto get a betterinsight into the sign of the lattice artifacts,for mp > 4 GeV. We mayproceedas

* This hasnot beendonehere, since it would introduce largerstatistical uncertaintiesthan the ones

obtainedwith ap.

C. A/exandrouet a!. / Boundson fB 269

follows:(i) Interpolatethe data, at a given value of a1.,, usinga smoothfitting-function

F~‘~“Fp(Mp):

F~(M~)+ ~tai iJ~(I + ~en(/3)M~). (8)

The asymptotic form FP(MP —~ cc) was constrainedby the hopping parameter

expansion[25]. In doing so,we expressedthe hoppingparameterK in termsof M~by the relation 1/(2K) = 1/(2K,.) + exp(M~— Mtlal) — 1 for M~>2. Z~

t~t,M~”tand K~are defined in ref. [13]. Eq. (8) enablesone to formally extrapolatethedataat the two largera-valuesup to m~— mB.

(ii) Determinelattice artifacts by fitting a linear ansatzin a, a~1F~=f~(m~)(1 + SM~),for eachm~,making useof the previousinter-(andextra-)polator.

Following this strategy, we again find that the lattice artifacts in eq. (5) arenegative for large enough values of m~,i.e. m~>4 GeV ~. Though we arereluctant to believe the actual size of finite-a corrections in a situation whereM~>3, we hold their sign to be trustworthy. It allows us to establish,from ourdataat a~= 3.35 GeValone(i.e. without any furtherreferenceto the form of thelattice artifacts), the lower bound f~(m

1,mb)> 213 MeV. As explainedbelow,this valuehasto be extrapolatedto the physicalB-meson,i.e. to really light quarkmasses,yielding the result

18OMeV<fB. (9)

Extrapolationto light quarks.In our calculationthe “light” quarkmasshasbeenkept fixed at a value correspondingto m~(m,..,m1) = 1.05 GeV. In order to findthe “true” valuefor the leptonic decayconstantof the physical B-mesonwe haveto correct for the unphysicalvalue of m0 usedso far. For the B-mesonBd and B~this meansextrapolationto zero m1, the correspondingdecay constantwill be

denotedby fB. In ref. [13] the calculationswere performeddown to light quarkmassesof the sizeof the strangequarkmass m~.From this datawe estimate

_~ 3f(m1, mh) —I0.010 GeV < <0.030 GeV

t9m~(m,,rn,)2

Using a Taylor expansion, this translatesinto the final result for the B-decayconstant:

188 MeV <fB <246 MeV. (10)

* The lowest-orderterm of the hopping parameterexpansionalone implies that lattice artifactsarenegativeat very largeM~.

270 C. A!exandrouet al. / Boundson f8

Theseboundscan evidentlybe tightenedby extendingthe computationsto lower

valuesof m,. For the B~decayconstantwe do not needto extrapolateasfar in thelight quarkmassandget

204 MeV <fe, <241 MeV

with a lower systematicerror.Finite-size effects. In ref. [131we found no volume dependencein varying L

from 0.7 fm and 1.05 fm. In the meantime,we have lattices of physical length

L = 1.5 fm [201andgranularitya,., = (1.53GeVYt Again no finite-sizeeffectsare

visible within the 10% statisticalerrors.So we concludethat finite-sizeeffectsareundercontrol.

Z-factors. In the perturbativerenormalisationof the lattice current one mayworry abouthigher-ordercorrections.We would like to stressthat 0(a) effectsinthecurrentrenormalisationare includedin our treatmentof lattice artifacts.Sincethe g2 termin the renormalisationis only 14%, the g4 effectsarenot expectedtobe large. They should thereforenot havea noticeableeffect on eqs.(9) and(10).

In the abovediscussionwe havetakeninto accountall but oneof the systematicerrors.The impact of the quenchedapproximationon the resultshas not beenestimatedso far. One has to wait for futureunquenchedcalculationsfor any realunderstandingof this latter uncertainty.Howeverwe do know that the quenchedlattice results for fK and f,. (after using eq. (6)) are in good agreementwith theexperimentalvalues.

3. Phenomenologicalconsequencesof a large lB

In this sectionwe will illustrate possiblephenomenologicalimplicationsof our

result,asgiven in eq.(10), on the expectedsize [7,18,191of CP violation effectsinB-decays.

As usual,we start from the unitarity triangle

associatedwith theb —‘ d transitions.Using the standardWolfensteinparametriza-tion we have J/~— IVCdVC~I + 1~’~d= 0 to a very good approximation[5,7]. Afterrescalingby I I — I this definesa triangle in the complexplanewith vertices(p, ~), (1, 0) and(0, 0) where

p=(ReJb)/IVCdV~I, i~=—(ImVb)/Il’~dJ’~I. (11)

C. Alexandrouetat / Boundson ~ 271

We usethe following phenomenologicalconstraint[5] *:

IVlb/V~bI_I1’~lSIl/p+fl_0.h1±0.05 (12)

with I 1”cb I = 0.044±0.009 and I I = 0.2205±0.0018,

the K°—K°CP-violatingparameter**

El =4.00X104BKIV~bI2IV~~l~[F(x,., x1) + ‘V~bI

2(1—p)F(x~)]

= (2.272±0.022)x i0~ (13)

andthe B°—B°mixing parameter

Xd = 4.15 x iO~BBrBm~f~I ~“~b 121 I 2(~ —p)2+ ~2)F(x~) = 0.71±0.11.

(14)

The value of eq. (12) is given in ref. [6] butwith a smallersystematicerror which

accordingto ref. [1] is unknown.Our value agreeswith the oneused in ref. [191.Thevalue for xd is obtainedfrom the weightedaverageXd = 0.166±0.033of theARGUS(updated)and CLEO results[5,61.

We follow ref. [19] andassumeBK = 0.94±0.11 andtakeBB = 1. The functionsF are the QCD correctedversionsof the Inami—Lim functionsdependingon thecharmmass x~= m~/M~and the top massx

1 = ~ [261.It it obvious fromthe expressionfor Xd that a large(small) valuefor fB favourspositive(negative)p.

Fig. 2 shows the allowed (p, ~) range for different values of m1, using thephenomenologicalconstraints(12)—(14). This figure shouldbe comparedwith fig.2.1 of ref. [3], which illustratesprevioustheoreticalprejudices.In fig. 3 wecomparethe allowedregionsfor thevertex(p, ~)of theunitarity trianglewhen fB is takenin the rangeof eq.(10) or in themore conventionalrangefB = 140±40 MeV. Thetop massis allowed to vary in the range

90GeV~m1~200GeV. (15)

This is the phenomenologicalbound from LEP, p~-colliderand neutralcurrentdata[271.

The CP-violating asymmetriesfor B-decaysinto CP eigenstatesareproportionalto sin 2c~,where 4 is one of the anglesof the unitarity triangle. Of particularinterest is the decayB —s J/i/i K~for which the CP asymmetryis proportionalto

* We remind the readerthat thesenumbersdependon theoreticalinputs.

** Assumingthe (‘PT invariance constraint4~=4÷..,we use el =4l~i÷_1(2+ I~’j/fl÷ I) andthe averagesLii÷.. I =(2.279±0.022)xi0~ and 3o()/~1~= 0.991±0.003[5].

272 C. A!exandrouet at / Bounds on fB

- s o~ ~ i 0

Fig. 2. Constraintsfrom I ~ / k~,I (dashedcircles), x~(dottedcircles),and I I (solid hyperbolas)onthe resealedunitarity triangle for 188 MeV( fB ~ 246 MeV and (a) m, = 90 GeV, (b) m,= 130 GeV,

and(c) m,= 200 GeV.

sin 2$ = 2sj(1 — p)/((l — p)2 + ~2) The allowed range is depictedin fig. 4. Thephenomenologicalboundsallow for substantiallylargervaluesof this quantity, inparticular if the top massis close to the present“central” value m~ 130 GeV.For example, from inspection of fig. 2b, one finds that large values of theasymmetrycomeout for positive valuesof p, which correspondsto the solutionfound in the phenomenologicalanalysisof ref. [181,

0.59<sin 2/3 <0.95, 0.09<p <0.38 for m~ 130 GeV. (16)

This is to be comparedto the situationwith conventionalfB’ wherep is definitelynegative:0.12> sin 2/3 <0.46; —0.63 <p < —0.22 for fB = 140 ±40 MeV at the

C. Alexandrouel a!. / Boundsonf~ 273

1.0’(a)

0.8’

1.:..~l.0 •(b)

0.8

0.6

Fig. 3. Allowed region (68% CL.) for (p, ~) for 90 GeV~m,~ 200 GeV (a) for large fB = 217±29MeV, favouring p> 0, and(b) for low fB = 140±40MeV, favouring p <0.

samevaluefor m~.Thus,for m1 around130 GeV andassumingthe p > 0 solution

to be realised,onewould gain some factor between1.3 and7.9 (!) in amplitude.Up to now a direct experimentalmeasurementof fB in the leptonic decay

B —f rv~is lacking. Theoretically,the branchingratio into this channelis given by

rn

2 2

Br(B—+r~~)= 5.41x 1012 GeV4IJ/~,bI2rBf~rnBrn~1— —j- (1 +SQED).mB

(17)

I. ~ ~o;o•. ‘~:~.. .

Fig. 4. Allowed region (68% C.L.) for the amplitude sin 2~relevant for the CP asymmetry inB —‘ i/I/I K, decays,The full line is for the high-f~range,andthedottedfor thelow-fB range.

274 C. A!exandrouet at / Boundson fB

Using parametersfrom ref. [5] and our lattice estimatefor fB (neglectingQEDcorrections)we get Br(B —s rv~)= 1.4 x i0” for the central value and a range(0.18to 6.1)x i0~ if we adduncertaintieslinearly. This result looksverypromis-ing and a direct measurementof fB appears to befeasible at LEP.

4. Summaryandconclusions

Within the quenchedapproximationwe havebeen able to perform a detailedstudyof the limiting behaviourof ~ near the static limit, m~—s cc~This hasbeenachievedby a conventional,non-staticcalculation,by varyingthe heavyquark

massmh andthe lattice spacingsa in suitableranges.Let ussummarizethe main results:

(1) The static limit in itself appears to be a poor estimatefor the B-mesondecay constant: the corrections of O(1/m~),as derived from the non-static

computations, amount to _ — 30% in the vicinity of the b-quark mass and—60% at the c-quarkmass.This implies thatwe cannotretrievethe scalinglaw

= const.(2) In our approachof treating lattice artifacts, we find the data — for all

a-valuesunderstudy— to be consistentwith eachother, evenwhenincreasingmhas high as mh 1.7 a~.We find large scalingviolationswithin the staticapproxi-mation,which canhoweverstill be describedby a first-orderansatz.

(3) The non-staticdata for f~,havebeen shown, by meansof extrapolationmh —p cc, to be in reasonableaccordwith the static approach[16].

As an upshotof this investigation,wecan for the moment(beforethe adventof

Teraflops computers)envisage two viable schemesto compute,by means ofextrapolation,the decayconstantof the B-meson~ in the limit a —* 0: (i) Eitherone attemptsto fit (and then unfold lattice artifacts by meansof extrapolationsfrom) non-staticresults takenbeyondthe D-range,or (ii) onerelies on non-staticresultscollected exclusively in the massrangebelow the D-meson(where, withpresentlyaccessiblelattices,heavyquarkscansafelybe handled)andsubsequentlyperformsextrapolationsfrom a fit constrainedto passthroughthe staticlimit, withfinite-a effectstakeninto accountin bothcases.In additionit would be helpful torepeatsuch a programwith an improved fermion action [281that is designedtoreduce0(a) scalingviolationsandhas beenusedsuccessfullyfor matrix elementsof thevectorcurrent[29].

In view of the phenomenologicalimportanceof fB to CP violation in the CKMscenario,it would be highly desirableto tightenthe boundsset in eq. (10). We arecurrently improving the precisionof the a,~= 3.35 GeV lattice results in order totest eq. (6) morestringently[20]. It will further be possibleto improve the bound(10) throughcalculationsat smaller(light-) quarkmassesanda smallervalueof thelattice spacing[30].

C. A!exandrou et a!. / Bounds on fB 275

Moreover,in this context, it is very important to explore the impact of quark

loopswithin full QCD.

We enjoyedinformative discussionswith L. Maiani, G. Martinelli, T. Nakada

and S. Narison.The numericalcalculationswerecarriedout on the CRAY X-MPof the ETH-Zürich,The CRAY 2 at Lausanneandthe CRAY Y-MP of theHLRZin Jülich. We thank the staff of theseinstitutionsfor their kind support.

References

[1] D.G. Hitlin, in Proc. SnowmassSummer Study on High-energyphysics, Snowmass,CO, 1990;CALTECH preprint CALT-68-1722(1991)and referencestherein

[2] N. Cabibbo,Phys.Lett. 10 (1963)513;M. Kobayashiand K. Maskawa,Prog.Theor. Phys.49 (1973) 652

[3] T. Nakada,ed., CERN Yellow ReportCERN 90-02(1990) andreferencestherein[4] P. Franzini, Phys.Rep.173 (1989)1;

E.A. Paschosand U. Türke, Phys.Rep.178 (1989) 145;T. Nakada,PSI reportPSI-PR-91-02

[5] ParticleData Group, J.J. Hernándezet al., Phys. Lett. B239 (1990) 1[6] B. Gittelman, in Proc.25th mt. Conf. on High-energyphysics,Singapore,1990, ed. K. PhuaandY.

Yamaguchi(World Scientific, Singapore,1991)[7] C. Dib, I. Dunietz, F. Oilman andY. Nir, Phys.Rev. D41 (1990)1522[8] T.M. Aliev andV.L. Eletsky, Soy. J. NucI. Phys.38 (1983)936;

V.S. Mathurand M.T. Yamazwaki,Phys.Rev. D29 (1984)2057;L.J. Reinders,H. RubinsteinandS. Yazaki, Phys.Lett. B104 (1981) 305; Phys.Rep. 127 (1985)1;Li. Reinders,Phys.Rev.D38 (1988)947;CA. Dominguezand N. Paver,Phys.Lett. B197 (1987)423; B246 (1990)493;S. Narison, Phys.Lett. B198 (1987) 104; in QCD spectralsum rules, World Scientific LectureNotesin Physics26 (World Scientific, Singapore,1989);A. Pich, Phys.Lett. B206 (1988) 322

[9] 5. Narison,Phys.Lett. B218 (1989) 238[10] M. Suzuki, Phys.Lett. B162 (1985) 392;

D. Silvermanand H. Yao, Phys.Rev.D38 (1988)214;S. Capstickand S. Godfrey, Phys.Rev. D41 (1990)2856

[11] E.V. Shuriak,NucI. Phys. B198 (1983) 83;MA. Shifman andMB. Voloshin, Soy. J. NucI. Phys. 45 (1988)292;H.D. Politzerand MB. Wise,Phys.Lett. B208 (1988)504

[12] MB. Gavelaet al., NucI. Phys.B306 (1988) 677; Phys.Lett. B206 (1988) 113;C. Bernard,T. Draper,G. HockneyandA. Soni, Phys.Rev.D38 (1988)3540;TA. Dc GrandandDR. Loft, Phys.Rev. D38 (1988)954

113] C. Alexandrou,S. Güsken,F. Jegerlehner,K. Schilling andR. Sommer,Phys. Lett. B256 (1991) 60[14] C. Bernardet al., NucI. Phys. B (Proc. Suppl.)20 (1991)488[15] E. Eichten,Nuct. Phys.B (Proc.Suppl.)4 (1988) 147[16] E. Eichten,NucI. Phys.B (Proc. Suppl.)20 (1991)475[17) C.R.AlIton et al., NucI. Phys.B349 (1991)598; NucI. Phys.B (Proc. Suppl.)20 (1991)504[18] J. Maalampi and M. Roos,Particle World 1(1990)148[19] M. Lusignoli, L. Maiani, G. Martinelli andL. Reina,Univ. di Romapreprint 792 (1991)[20] C. Alexandrous,S. Güsken,F. Jegerlehner,K. Schilling and R. Sommer,in preparation[21] L.H. KarstenandJ. Smit, NucI. Phys.B183 (1981)103;

R. Groot,J. Hoek andand J. Smit, NucI. Phys.B237 (1984)111;M. Bochicchio,L. Maiani, 0. Martinelli, G.C. Rossiand M. Testa,NucI. Phys.B262 (1985) 331

276 C. A!exandrouet a!. / Boundson fB

[22] G. Heatlie et al., RomeUniversitypreprint737 (1990)[23] S. Cabasinoet al. (APE group). NucI. Phys. B (Proc. Suppl.)20 (1991)399[24] R. Sommer,PhD thesis, preprintWU-B-86;

K. Schilling and R. Sommer,Z. Phys. C29 (1985)95;C. Michael and M. Teper,NucI. Phys.B314 (1989)347

[25] KG. Wilson, in New phenomenain subnuclearphysics,Erice, 1975, ed. A. Zichichi(Plenum,NewYork, 1977);A. Hasenfratz,Z. Kunst, P. Hasenfratzand C.B. Lang,Phys. Lett. BilO (1982)289

[26] T. Inami andCS. Lim, Frog. Theor. Phys.65 (1981) 297 [Erratum: 65 (1981)1722];Y. Nir, NucI. Phys.B306 (1988) 14;WA. Kaufman,H. Stegerand Y.P. Yao, Mod. Phys.Lett A3 (1988)1479;WA. KaufmanandY.P. Yao, Phys. Rev. D39 (1989)3373;A. Datta, J. Frdlich and E.A. Paschos,Z. Phys.C46 (1990)63;A.J. Buras,M. JaninandPH. Weisz,NucI. Phys.B347 (1990)491

[27] F. Dydak, in Proc. 25th Int. Conf. on High energyphysics, Singapore,1990, ed. K. Phua and Y.Yamaguchi(World Scientific, Singapore,1991);J. Ellis andG.L. Fogli, Phys.Lett. B249 (1990)543;P. LangackerandM. Luo, Univ. of Pennsylvaniapreprint UPR-0466T(1991)

[28] B. SheikholeslamiandR. Wohlert, NucI. Phys.B259 (1985)572[29] E. Gabrielli et al., NucI. Phys. B (Proc. Suppl.)20 (1991) 448130] A. Abada,Ph. Boucaud,J. Galand,0. Pene,M. Crisafulli, G. Martinelli, R. Sarno,S. Güsken,K.

Schilling and R. Sommer,in preparation