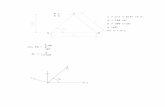
Solve: 1. m + 3 = 10 11. 3a = 18 21. m + 12 = 12 31. 8m = 5 2 ...

Solve: 1. m + 3 = 10

11. 3a = 18 21. m + 12 = 12 31. 8m = 5

2. a + 10 = 20

12. 2b = 8 22. n + 7 = 3 32. 3a = 2

3. m + 7 = 14

13. 5p = 15 23. c – 5 = -4 33. 12y = 8

4. p + 5 = 15

14. m ÷ 3 = 2 24. w – 10 = -12 34. 4m = -16

5. a – 2 = 10

15. a ÷ 2 = 10 25. g + 6 = -2 35. 6a = -12

6. a – 5 = 20

16. m ÷ 7 = 3 26. h + 10 = -10 36. -3m = 18

7. n – 4 = 16

17. a4 = 2

27. f – 15 = -15 37. r5 = – 2

8. 6 + n = 12

18. m6

= 3

28. r – 8 = 6.7 38. m10

= – 7ꞏ3

9. 10 + m = 13 19.

m9

= 10

29. r - 3 12 = -30 39. -7n = 49

10. 5m = 20

20. p5 = 0

30. -4 + w = -12 40. r10

= – 6ꞏ9

1. 2a + 1 = 5

6. 1 - 4m = 13 11. 3w + 4 = 13 16. 2a – 3 = 15

2. 3m + 2 = 8

7. -2a - 6 = 12 12. 12 - 4q = 16 17. 5y – 3 = 7

3. 2a + 7 = 13

8. 3g + 5 = 17 13. 3a -11 = 1 18. 2a – 12 = 10

4. 3n – 2 = 7

9. 2m – 4 = 12 14. 15 - 2m = 11 19. 8a + 4 = 20

5. 5k – 1 = 24

10. 7h – 2 = 12 15. 5q - 20 = 0 20. 7m + 9 = 30

1.) 6x - 5 = 13

A

2.) -4 + 2x = 18

E

3.) 7x - 6 = 8

B

4.) 4x - 10 = 30

U

5.) 8x - 1 = 7

V

6.) 3x - 5 = 7

F

7.) 10x - 5 = 65

C

8.) 6x - 2 = 46

I

9.) 2x - 2 = 22

G

10.) 3x - 4 = 11

N

11.) 5x - 5 = 25

T

12.) -6 + 2x = 12

S

Joke Why is six afraid of seven ? Answer:

2 11 7 3 10 9 11 9 11 1 11 5 3 6 11 5 8 5 11

!

Perimeter/Area - Find a Word

WORDLIST

CIRCUMFERENCE

PARALLELOGRAM

PERPENDICULAR

ESTIMATION

MEASUREMENT

LENGTH

RECTANGLE

AREA

ARC

KITE

PERIMETER

SECTOR

RHOMBUS

BREADTH

TRIANGLE

TRAPEZIUM

UNITS

HECTARE

HEIGHT

RADIUS

SQUARED

CIRCULAR

DIAMETER

COMPOSITE

QUADRANT

C A E C R O R E T E M I R E P

E P E R P E N D I C U L A R A

E A C T E E I A R R O T C E S

S R C O N T C E S U I D A R C

H L T I A C C E K I T T U T N

K L T I R P R E P R S I S C T

E L I T C Q L U O M N U M N R

R E R H T U U T F A I E B A A

E G N N H K R T I T K C H L A

T O A G E S A Q A R U Q O G D

A A L L C O M P O S I T E I Q

M R G E E T I K I T I K R E U

D E R A U Q S B R E A D T H T

I M E L N M U I Z E P A R T C

A R E A T N E M E R U S A E M

Find the words in the puzzle from the wordlist.

© FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

Units of Measurement

When units of measurement are changed, multiply or divide by 10, 100, 1 000 or more. To change to a smaller unit multiply, to convert to a larger unit divide. Some students have difficulty with this, they think that if the unit is larger you must multiply. This isn't the case. Imagine you have 1 m or 100 cm, both are the same distance, there are more of the smaller unit, 1 100, so:

changing to a smaller unit means - multiply changing to a larger unit means - divide

The number used to multiply or divide is the number of small units in the larger unit. For example 2 m to cm, there are 100 cm in a metre, changing to a smaller unit so multiply�so multiply by 100. As only 10, 100 or 1 000 are used to get the answer � move the decimal point. Multiply by 10 move the decimal place 1 position to the right, 100 move 2 positions and 1 000 move the decimal place 3 positions to the right. Division is the same number of moves, only this time it�s to the left. Divide by 10 and move the decimal place 1 position to the left, 100 move it 2 positions and 1 000 moves 3 positions to the left. A reminder is at the top of each column. Column 1 starts with changing mm to cm. You should be able to talk it through to your-self�.mm to cm is changing to a larger unit...that means division�.there are 10 mm in a cm that means I divide by 10�.divide by 10 means I move the decimal point 1 place to the left. That means 18 mm = 1.8 cm 113 mm = 11.3 cm and 0.9 mm = 0.09 cm. The next part of the column is the reverse, multiply by 10 means move the decimal place 1 position to the right. So 54 cm = 540 mm, 1.3 cm = 13 mm and 123 cm = 1 230 mm. Column 2 deals with converting between cm and m. This time the change is by dividing or multiplying by 100. That means a 2 decimal place movement. For cm to m (divide by 100) 12 cm = 0.12 m, 106 cm = 1.06 m and 5.78 cm = 0.0578 m. Then the reverse, m to cm means multiplying by 100 or a 2 decimal place shift to the right: 3 m = 300 cm, 0.7 m = 70 cm and 10.05 m = 1 005 cm. Column 3 is m to km, this involves multiplying or dividing by 1 000, or a 3 decimal place movement. That would mean 300 m = 0.3 km, 2 305 m = 2.305 km and 4.7 m = 0.0047 km. Then the reverse, changing km to m. That�s 3 decimal places to the right: 1.2 km = 1 200m, 0.85 km = 850 m and 0.02 km = 20 m.

Units of Measurement

2 50 mm

3 130 mm

4 55 mm

5 92 mm

6 200 mm

7 18.6 mm

8 2 020 mm

10 0.95 mm

9 435 mm

1 20 mm

11 5.47 mm

12 906.2 mm

Convert these lengths from mm to cm

10 mm = 1 cm 1 place left

14 18 cm

15 6.3 cm

16 74.8 cm

17 356.7 cm

18 8.12 cm

19 0.4 cm

20 0.566 cm

22 829.3 cm

21 155 cm

13 5 cm

23 1.002 cm

24 19.91 cm

Convert these lengths from cm to mm

1 cm = 10 mm 1 place right

Convert these lengths from cm to m

100 cm = 1 m 2 places left

26 600 cm

27 150 cm

28 370 cm

29 12 cm

30 86.5 cm

31 7 300 cm

32 56.05 cm

34 6.7 cm

33 3 cm

25 200 cm

35 8 002 cm

36 27.08 cm

Convert these lengths from m to cm

1 m = 100 cm 2 places right

38 7 m

39 2.2 m

40 5.9 m

41 0.3 m

42 0.75 m

43 0.363 m

44 5.02 m

46 0.006 m

45 10.7 m

37 3 m

47 5.071 m

48 30.262 m

Convert these lengths from m to km

1 000 m = 1 km 3 places left

50 1 220 m

51 4 930 m

52 110 m

53 550.6 m

54 1 003 m

55 85 m

56 4.7 m

58 12 032 m

57 309.7 m

49 1 500 m

59 8 771.3 m

60 763.2 m

Convert these lengths from km to m

1 km = 1 000 m 3 places right

62 8 km

63 3.2 km

64 14.7 km

65 10.6 km

66 0.9 km

67 0.673 km

68 5.12 km

70 0.4503 km

69 1.007 km

61 3 km

71 4.019 km

72 0.06 km


Perimeter of Shapes

The perimeter of a shape is the distance around the outside of the shape. The units of measurement are mm, cm, m and km. Shapes often have side lengths that are the same, rather than writing this distance out again a mark is put on the identical sides to show they are the same length. If there are a number of different pairs of sides that are the same length, 2 marks together will be used and so on, such as with a rectangle. To answer columns 1 and 2 use the same method, this is:

Look at the side markings and write side lengths on every side it is up to you if you write the units as well The first line of working is the sum of the sides of the shape, write �P =� then the sides separated by + signs. Note that to avoid missing sides don't jump around in the addition.

Start on a side then move around the shape in a clockwise or anti-clockwise direction. If the sum is challenging to complete mentally, total the sum as you move through, look at the example below. The second line is the answer line, again write �P =� then the answer, then the units, either mm, cm or m.

Column 3 introduces formulae used for squares and rectangles. These are:

Squares: P = 4l (which is 4 times the side length) Rectangles: P = 2l + 2b (which is 2 times the length + 2 times the breadth)

The questions are in tables. With squares, multiply the side length by 4 and write the answer with units. The rectangles are completed in stages, l is given and you double it to get the value of 2l, b is given and you double it to get the value of 2b. Then add the values for 2l and 2b together to get the answer, write in the units (all of which are cm.)

7 m

7 m

7 m

7 m

7 m

7 m

P = 7 + 7 + 7 + 7 + 7 + 7

P = 42 m

Fill in all the side lengths to avoid

missing them

Perimeter of Shapes

Put measurements on all sides then add them to find the perimeter.

4

7 m

2

11 m

25 m

1

6 cm

P = cm

P = 6 + + +

3 8 mm

30 mm

5

16 mm

9 mm

Complete the tables, all measurements are in cm.

Length(l)

Perimeter (4l)

Length(l)

Perimeter (4l)

5 20 cm 15

8 11

10 14

9 30

3 50

4 80

12 55

20 42

8 11

Length(l)

2l Breadth

(b) 2b

Perimeter (2l + 2b)

14 28 5 10 38 cm

12 5

9 6

15 25

20 16

7 19

13 17

10

2 m

6 m 12 m

22 m

6

1.3 cm

7

2.1 m

8

15 mm

9 mm

22 mm

5 m

13 m

3 m

9

11

8 cm

P = ×

13

Perimeter Formula for Squares :

P = 4l where l = side length

5 cm

= 4 × 5

P = 20 cm

P = 4l

12

Perimeter Formula for Rectangles :

P = 2l + 2b where : l = length and

b = breadth

P = 2l + 2b

14 cm

5 c

m

= 2×14 + 2×5

P = 38 cm


Perimeter of Shapes

The perimeter of a shape is the distance around the outside of the shape. The units of measurement are mm, cm, m and km. Shapes often have side lengths that are the same, rather than writing this distance out again a mark is put on the identical sides to show they are the same length. If there are a number of different pairs of sides that are the same length, 2 marks together will be used and so on, such as with a rectangle. To answer columns 1 and 2 use the same method, this is:

Look at the side markings and write side lengths on every side it is up to you if you write the units as well The first line of working is the sum of the sides of the shape, write �P =� then the sides separated by + signs. Note that to avoid missing sides don't jump around in the addition.

Start on a side then move around the shape in a clockwise or anti-clockwise direction. If the sum is challenging to complete mentally, total the sum as you move through, look at the example below. The second line is the answer line, again write �P =� then the answer, then the units, either mm, cm or m.

Column 3 introduces formulae used for squares and rectangles. These are:

Squares: P = 4l (which is 4 times the side length) Rectangles: P = 2l + 2b (which is 2 times the length + 2 times the breadth)

The questions are in tables. With squares, multiply the side length by 4 and write the answer with units. The rectangles are completed in stages, l is given and you double it to get the value of 2l, b is given and you double it to get the value of 2b. Then add the values for 2l and 2b together to get the answer, write in the units (all of which are cm.)

7 m

7 m

7 m

7 m

7 m

7 m

P = 7 + 7 + 7 + 7 + 7 + 7

P = 42 m

Fill in all the side lengths to avoid

missing them

Perimeter of Shapes

Put measurements on all sides then add them to find the perimeter.

4

7 m

2

11 m

25 m

1

6 cm

P = cm

P = 6 + + +

3 8 mm

30 mm

5

16 mm

9 mm

Complete the tables, all measurements are in cm.

Length(l)

Perimeter (4l)

Length(l)

Perimeter (4l)

5 20 cm 15

8 11

10 14

9 30

3 50

4 80

12 55

20 42

8 11

Length(l)

2l Breadth

(b) 2b

Perimeter (2l + 2b)

14 28 5 10 38 cm

12 5

9 6

15 25

20 16

7 19

13 17

10

2 m

6 m 12 m

22 m

6

1.3 cm

7

2.1 m

8

15 mm

9 mm

22 mm

5 m

13 m

3 m

9

11

8 cm

P = ×

13

Perimeter Formula for Squares :

P = 4l where l = side length

5 cm

= 4 × 5

P = 20 cm

P = 4l

12

Perimeter Formula for Rectangles :

P = 2l + 2b where : l = length and

b = breadth

P = 2l + 2b

14 cm

5 c

m

= 2×14 + 2×5

P = 38 cm


Perimeter Problems

5 given small garden areas. The plots all occupy the same land area (16 m²) but have different side lengths, find the perimeter of each.

Three hobby farmers are each

Plot 1 : 16 m by 1 m

Plot 2 : 8 m by 2 m

Plot 3 : 4 m by 4 m

6 had to pay to fence the area, would it be cheaper to have a square area or a rectangular area?

If you were offered a plot and

Circle : square or rectangle

7 as shown below. Calculate the length of the string A and string B, then add them to find the total length.

A parcel has 2 strings around it

10 cm

A

B

6 cm 30 cm

A:

B:

8 the side length of a square you get 4 times the perimeter, is he right?

Scott says that when you double

For Not a

9 2 buses, lined up end to end (see below). Dan is superstitious and walks 1 lap around the buses before the jump, how far does he walk?

Dare-devil Dan is about to jump

The buses are 11 m long and 3 m wide

11 m

10 material that will stretch to 18 times its length before breaking. If the original length is 7 m, find its maxi-mum length. Will it stretch around a rectangular building with sides 25 m and 35 m? (Find P then circle answer)

An inventor created a synthetic

Max length

Yes / No

11 around the perimeter of the backyard when he sees Leon arrive home. Find the distance he runs around the empty yard. Then calculate the distances he runs when Leon's car is in position A or in position B, (not both together). Leon's car is 2 m wide and 5 m long.

Leon's dog 'Oblong' always runs

Position A is in the centre of the yard

17 m

8 m A

B

No car:

Car B :

Car A :

Answer the perimeter problems below.

1 has sides with lengths 12 m and 4 m. Find the distance around the pool.

A rectangular swimming pool

2 same pool (Q1) calculate the length and breadth of the pool and the path combined, put the dimensions on the diagram below and find the perimeter

A path 1 m wide surrounds the

3 safety fence around the outside of the path find the cost of fencing the pool when the fence costs $27 per metre.

If the pool above has a

4 noted that on average an ant stopped every 5 cm. If the viewing tray was 30 cm by 20 cm, find its perimeter.

In a science experiment Travis

i) in 1 lap

ii) in 5 laps

iii) over a 9 m distance

How many times would the ant stop:


Changing Units of Area

This is one of the easiest parts of area calculations to make a mistake. Students often forget this work. The reason is that because there are 10 mm in 1 cm, students automatically use this to convert mm² to cm², but this isn't the case. There is infact 100 mm² in 1 cm². The same with converting cm² to m², there is 10 000 cm² in a m², not 100 cm². Column 1 first converts areas from cm² to mm². Note the diagram at the top of the column. A 1 cm square is redrawn with grid lines at each millimetre. The square has 10 mm sides and as you know the area of a square is its side length squared. As 10² = 100 there are 100 1 mm² squares in a square cm. So to convert the measurements multiply each number by 100. This means move the decimal point 2 places to the right. So 5 cm² would be 500 mm², 5.5 cm² would be 550 mm² and 5.05 cm² would be 505 mm². Questions 11- 20 are the reverse, move the decimal point 2 places to the left. So 8 mm² is 0.08 cm², 130 mm² is 1.3 cm² and 130.02 mm² would be 1.3002 cm². Column 2 then deals with converting between m² and cm². Look at the diagram and note that the same method is used to calculate that there are (100 × 100) 10 000 cm² in 1 m². So to change cm² to m² multiply the number by 10 000 or move the decimal point 4 places to the right. So 8 m² would be 80 000 cm² and 8.02 m² would be 80 200 cm². Then the method is reversed for the second part of the column. When you divide by 10 000 move the decimal place 4 places to the left. So 9 cm² would be 0.0009 m² and 136 cm² would be 0.0136 m². Column 3 are worder questions that you solve using the units as given in the question. Then after you answer the question express the answer in the other unit that is requested.

Changing Units of Area

Convert these areas from cm² to mm²

1 cm² = 100 mm²

=

10 mm

10 mm

1 cm

1 cm

1 3 cm²

2 8 cm²

3 7.5 cm²

4 18 cm²

5 29 cm²

10 100.1 cm²

6 45.6 cm²

7 65.32 cm²

8 82.09 cm²

9 100 cm²

Convert these areas from mm² to cm²

1 mm² = 0.01 cm²

=

10 mm

10 mm 1 mm²

11 5 mm²

12 10 mm²

13 25 mm²

14 125 mm²

15 170.1 mm²

20 500.6 mm²

16 205.4 mm²

17 30.03 mm²

18 450 mm²

19 500 mm²

Convert these areas from m² to cm²

1 m² = 10 000 cm²

=

1 m

1 m

100 cm

100

cm

21 2 m²

22 3 m²

23 0.3 m²

24 0.03 m²

25 3.3 m²

30 0.0009 m²

26 0.725 m²

27 0.203 m²

28 0.8963 m²

29 0.902 m²

Convert these areas from cm² to m²

1 cm² = 0.0001 m²

=

100 cm

100

cm

1 cm²

40 15 796 cm²

31 7 cm²

32 11 cm²

33 54 cm²

34 154 cm²

35 296 cm²

36 875 cm²

37 1 500 cm²

38 8 700 cm²

39 12 000 cm²


41 size 1.5 m × 2.7 m. Find its area in m² and then convert to cm².

A rectangular piece of fabric is

A = lb

Fabric area:

cm²:

m²:

The size of the plate

A square steel plate with sides 8.2 cm has a rectangular slot cut into it with sides 52 mm and 14 mm. Find:

44

Plate area:

mm²:

cm²:

The size of the slot. 45

Slot area:

cm²:

mm²:

The total area of the plate 46

mm²:

cm²:

42 and 85 cm. Find its area in cm2, then convert this to m2.

A kite has axis lengths of 58 cm

43 length of 2.2 m and a height 4.1 m. Find the area of the sail in m2 & cm2.

A triangular sail has a base

Sail area:

cm²:

m²:

Answer these questions using the methods from the first two columns. Answer to 2 d.p.

A = l²

Kite area:

m²:

cm²:

Area of Squares and Rectangles

The area of a square and rectangle is found in the same way. Multiply one side by the other. As squares have sides all the same length, this means you just �square� the side length. While the answer isn�t affected, the length is usually considered the longest length in a rectangle. Examples - Find the area to 1 decimal place. In the 2nd column watch for units requiring conversion. Always change the units before multiplying, don�t multiply the numbers as they are, then change the answer. Area conversion is more difficult than length conversion. The last two questions in the third column have the area given, you have to find the side lengths. When finding the side length of a square, square root the area. With rectangles, given one side and the area, divide the area by the given side.

Square A = l2 Rectangle A = lb

l l

b

A = 292.4 cm2 (1 d.p.)

A = l2

= 17.12

Write the formula

Substitute l (or l & b)

Solve showing square units. Round to 1 decimal place.

17.1 cm 25.2 m

13.3 m

A = 335.2 m2 (1 d.p.)

A = lb

= 25.2 × 13.3

Area of Squares and Rectangles © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

Use A=l2 to find the area of these squares, to 1 d.p. Show a 2 as area is in square units.

1 A = l2

9 cm

= 2

2

A =

A = cm2

3

2.4 m

4

13.6 m

11.7 mm 5

6

7

83.9 cm

8

1.4 km

7.5 km

Now rectangles. Use A=lb to find the area, round to 1 d.p. when required.

9 A = lb

=

A =

×

8 cm

5.5

cm

10

11

15.3 m

40.7

m

20.3

mm

6.7 mm

12

13

2.5 km

390 m

Answer in km2

82 mm

11.3 cm

Answer in cm2.

14

15

In mm2.

In m2.

705 m

1.06 km

54.7 cm

317 mm

Apply your area skills to these questions.

16 How much would it cost to tile a square room with sides of 3.5 m, if tiles cost $73.20/m2 ?

17 A rectangular field has sides 980 m and 660m. Find its area in ha given 1 ha = 10 000 m2.

18 Office paper often weighs 80 grams per m2. Find the weight of an A4 sheet, which has sides 29.7 cm and 21 cm. Answer to the nearest gram.

19 A square has an area of 275.56 cm2. What is its side length?

20 A rectangle has an area of 630.8 mm2. Find its breadth in cm if it has a length of 16.6 mm.

A = cm2

12 cm

Calc: 9 x2 =

Cost =

Cost =

Area of Triangles

The area of a triangle is found by �half times the base times the perpendicular height.� A triangle is half of a rectangle, so it makes sense that the formula is the same as that of a rectangle except it is halved. Note that the height is the perpendicular height, the base and the height must always be at right angles to each other. Below is an example of finding the area of a triangle. Column 1 asks you to find the area for a triangle. Remember to watch for units. Column 2 continues finding the area of a triangle but this time you have to select which numbers you multiply, remember that the height must be perpendicular to the base length. The end of column 2 and start of column 3 has two worded questions for you to attempt. Column 3 then has a field that has been broken up into separate areas. Find the areas of the triangles, square and rectangle. Add them together for a total area for the field.

Triangle A = ½bh

Where: b = base length h = perpendicular height

A = 60 cm2

A = ½bh

= ½ × 8 × 15

Write the formula

Substitute b and h

Solve showing square units. Round answer if required.

15 c

m

8 cm

h

b

Area of Triangles © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

1

2

A =

A = m2

3

4

Find the area of these triangles. Units are square units, e.g. cm2.

9 cm

8 cm

A = ½bh

=

A = cm2

½× ×

Calc: 0 . 5 × 9 × 8 =

3.4 m

5.2

m

43 mm

55 m

m

14 m

8.2

m

5

6

13.9 km

5.6 cm

10.7

cm

7

8

46 mm

68 m

m

7.2 cm

12.4

cm

20.6

km

Find the area of this field, it is broken up into triangles, squares and rectangles. All lengths in m.

19

22

10

24

19

19

24 20

14

A1

A2

A3

A4

A5

A6 25

17

A1 = ½bh

A1 = m2

A2 = lb

A2 = m2

A3 =

A4 =

A4 = A3 =

A5 = l 2

A6 =

A6 = A5 =

Area =

Find the area of these triangles. Cross out the lengths you don�t need to use.

9

10

9 cm

11

12

13

12 c

m 15 cm

10 cm

12 c

m

13 c

m 13 cm

2.7 m

5.2 m

2.9 m

2 m

84 mm

245

mm

259 mm

56 cm

53 c

m

53 cm

45 cm

Now apply your skills to these.

14 Find the area of a triangular

15 triangle. It is 3.3 m high and has a 2.1 m base. Find the sail area.

A yacht jib is a right angled

16 agrees to pay $8 000 per m2 of the jib. Find the cost to sponsor the full jib for the yacht above.

A race sponsor of the yacht

paddock with base 205 m and �height� 307 m, convert the area to hectares (2 d.p.) 1 ha = 10 000 m2

The Circle (Sheet 1)

This sheet deals with naming parts of a circle, these are areas of circles created by particular lines and also the lines themselves.

Column 1 starts with matching diagrams showing the features of the circle with the words on the right of the column. Draw a line between the diagram and the correct word. The areas and lengths are shown below.

Column 2 asks you to draw lines between points on the circle, this will create areas. Name the lines (using words like radius, diameter ….) as well as the areas.

Questions 29 and 30 require you to draw the lines and label points yourself, you will need a protractor to answer question 30.

Segment (minor)

Semi-circle

Sector

Quadrant

Circle Areas

Circumference

Tangent

Radius

Diam

eter

Chord

Arc

Circle Lengths

The Circle (Sheet 1)

The diagram on the left shows a shaded area or a feature in black. Match the diagram with the list on the right, using a ruler to draw a line between the two black dots.


6

4

5

3

2

1

7

8

9

10

11

12

13

Sector

Centre

tangent

Quadrant

Major Sector

Radius

Minor Segment

Arc

Diameter

Chord

Circumference

Semi-Circle

Major Segment

Given points on each diagram, draw the intervals and then name the features. Use the word list in the left column for help.

14 Connect O to A, then O

to C and shade the two areas.

A

O C

1

2

15 Area 1

16 OA

17 AC 18 Area 2

19 Connect A to B and

shade the two areas.

A

B

1

2

20 Area 1

21 AB

22 AB 23 Area 2

Straight line

Curve

24 Draw a straight line

BOC, then perpendicular OA

A

25 Area 1

26 BC

27 OA 28 Area 2

O

B C1

2

Use the circles below to make the following constructions.

29 Plot a point ‘C’ on the

circumference of the circle, draw a tangent touching the circle at C. Draw a line from C to the centre of the circle O.

30 Name the point ‘O’ at

the centre of the circle. Draw two radii, OA and OB, with an acute angle between the two. Plot a point C away from points A and B. Draw chords AC & BC. Protractor?

AOB = ACB =

Circumference (Sheet 1)

The circumference of a circle is its perimeter, the distance around the outside of the circle. This distance is found by using this formula:

C = 2 r Where: C = Circumference of circle r = radius of the circle

Column 1 uses the above process for all questions. Column 2 gives you a diameter rather than a radius. So you can divide by the diameter by 2 to find the radius then use C = 2 r, but an easier way is to use:

C = d Where: C = Circumference of circle d = diameter of the circle (note that d = 2r) Column 3 are problem style questions using the circumference of a circle.

Example C = 2 r

= 2 × × 15

C = 94.2 cm (1 d.p.)

15 cm

Write the formula.

Show × signs and replace r with the radius (15 on diagram).

Calculate, round and show units.

Calculator 2 × × 5 = Answer on Screen 94.24777961

Round to 1 decimal place 94.2 cm (1 d.p.)

1

Circumference (Sheet 1)

These use diameter. Either divide by 2 for the radius OR use C= d. Answer to 2 d.p.

Now apply your skills to these problems. Answer to 2 d.p. where appropriate.

Use C=2 r to find the circumference of these circles to 1 decimal place.


Example

C = 2 r

= 2 × × 17

C = 106.8 cm

17 cm

Write formula

Substitute value for r

Answer 1 d.p., show units

1

2

3

4

5

6

7

4 m

63 mm

8.8 m

19.7

cm

42.5 km

172 mm

9½ cm

8

52 cm

9

10

196

mm

11

12

13

14

15

7.6 m

= 35 cm

= �phi� = d *

1.19

km

5.07 m

125 mm

= 7.89 m

16 A car tyre has a diameter of 63 cm. Find its circumference. Give your answer in metres.

17 How far does the tyre travel when it rotates 150 times?

18 How many complete rotations of the tyre will occur if 1 km is travelled?

Conveyor Belt

85 c

m

14 cm

19 Calculate the amount of conveyor belt fed by 1 rotation of the drive wheel.

Drive wheel

Idler wheel

1 rotation of the idler wheel 20

Complete: 21

C (Drive)

C (Idler)

= =

Fractions of a Circle and Arc Length

This sheet finds the length of an arc of a sector. The arc is the curved length which is a fraction of a whole circle�s circumference. So in other words, this sheet deals with the circumference of a circle but multiplied by a fraction. Column 1 starts with sectors (including quadrants and semi-circles) and finding the fraction of the circle that they represent. This requires you to identify the internal angle and write it �over� 360°. That answers the question but the next step is to simplify the fraction. This can be done in your head by dividing by the LCM, or using a calculator. Example Column 2 relates the fraction to the arc length. The circumference of a circle is C = 2 r, but as these are sectors then the arc length is a fraction of the circumference (if the circle was whole). Where: l = the arc length (curved length) = the internal angle of the sector r = radius of sector Example Column 3 asks you to find the perimeter of the sectors. So the method is just the same as above, but then add on the straight lengths as well. The straight lines are the radii, there are two of them. So work out the arc length, add two radii and you are done.

55

360 =

11

72 55°

÷ 5

÷ 5

Calculator 5 5 ab/c 6 0 =

Answer on Screen 11

3

72 But you write 11

72

l = 360

× 2 r

l = 64.3 m (1 d.p.)

l = 360

× 2 r

= 360

335 × 2 × × 11

11 m

335°

l = 360

× 2 r + 2r

Fractions of a Circle and Arc Length

Find the fraction of a circle and multiply by 2 r to find the arc length �l� to 1 d.p.

1


Calculate the fraction of a circle shown by these sectors, simplify if possible.

360 =

4

2

360 =

3

=

5

=

4

=

60°

240°

6

=

140°

7

=

300°

8

=

25°

9

=

200°

10

43 cm l = cm

l = 360

× 2 r

= 360

× 2 × ×

l =

l = 360

× 2 r

=

× 2 × ×

11

3.8 m

12

86 mm

13 60 cm

120°

14

15

50° 39 km

5 m

320°

Now find the perimeter, to 1 d.p. Include the radii.

l =

l = 360

× 2 r + 2r

= 360

× 2 × × + 2 ×

16 2.3 m

17

210°

37 mm

18

19

13.2 cm

122°

7.9 m

Perimeter of Composite Shapes

This sheet shouldn�t be attempted before the previous sheet on Arc Length is attempted. The circumference of a circle is found by C = 2 r or C = d. But with composite shapes parts of a circle are involved with other shapes/lengths, so you need to use fractions to find the arc length, then add that length to the other sides of the shape. Example - Finding the perimeter to 1 d.p.

This sheet is answered by the above method, except sometimes quadrants are involved. So instead of using 1/2 you will use 1/4 to find the arc length. Column 3 has the last two questions requiring an extra step, these require Pythagoras Theorem before solving.

2.4 m l1 = 3.8 m

l1 = 1/2 × d

= 1/2 × × 2.4

P = 3.8 + 7.5 + 2.4

l2 = 7.5 m

l2 = 1/2 × d

= 1/2 × × 4.8

P = 13.7 m

l1

l2

Label l1 on the diagram and calculate the arc length.

Label l2 on the diagram and calculate the arc length.

Add the three lengths. That is the two arc lengths and the 2.4 m straight length.

Perimeter of Composite Shapes © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

Find the perimeter to 1 d.p.

1

7 cm

2

28 m

11 m

3

9 cm 12 cm

15 c

m

4

5

47 cm 38

cm

6

53 cm 53 cm 1.4 m

1.65 m

Pythagoras required, round to 2 d.p.

8

7

9

0.5 m

73 mm

165 mm

l =

l = 1/4 × 2 r

= 1/4 × 2 × ×

P =

P =

cm (1 d.p.)

+ 4 ×

cm

28 m

5 m

Area of Parallelograms and Rhombuses

A parallelogram looks like a rectangle that has been pushed. A rhombus, also called a diamond, looks like a square that has been pushed over. So a parallelogram has two pairs of parallel sides of the same length, like a rectangle. A rhombus has four sides all the same length, with two pairs of parallel sides.

Below are two examples. What happens if you aren�t given the diagonals of a rhombus, but instead base and its perpendicular height? Solve just like it is a parallelogram. By definition all rhombuses (or rhombi) are parallelograms.

Rhombus A = ½ xy Parallelogram A = bh

x

y

h

b

Where: x and y are the lengths of the diagonals.

Where: b = base length h = perpendicular height

A = 204 cm2

A = ½ xy

= ½ × 17 × 24

Write the formula

Substitute x & y (or b & h)


A = 335.2 m2 (1 d.p.)

A = bh

= 25.2 × 13.3

24 cm

17 cm

25.2 cm

13.3

cm

Area of Parallelograms and Rhombuses © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

A rhombus is like a square that has been pushed over. Find the area, 1 d.p. when needed.

Find the area of these parallelograms. Round to 1 d.p. if needed.

Example Example

A = bh

= 17 × 8

A = 136 cm2

1 2

4

3

6

5

8

7

Find the area in cm2.

A = bh

A =

A =

×

cm2

17 cm

8 cm

22 cm

13 cm

7.3 m

5.6

m

38 mm

65 mm 4.7

m

14 m

65 cm

1.2 m

87 mm

124 mm

96 cm

1.30

7 m

0.20

8 m

382 mm

Calc: 0 . 5 × 2 2 × 4 7 =

A = ½ xy

= ½ × 47 × 22

A = 517 mm2

47 mm

22 m

m

9 10

12

11

14

13

16

15

All units are in cm.

A = ½ xy

A =½ × ×

A = cm2

18 cm

11 cm

0.9 m

1.7 m

4

391 mm

82 mm

73 mm

165 mm

9 9

11

11

4

25

25

24

24

27

27 2

2

23

23

Area of Kites and Trapeziums

A kite is the easiest shape to remember because its name is the same as the kite that you see flying. To find its area the same formula as the rhombus formula is used, that is, its internal diagonal lengths are multiplied together and by a half. Trapeziums are similar to rectangles in a way. The height is the perpendicular height like in a rectangle, but the base is the average of the top and bottom lengths. This average is then multiplied by the height. The formulae are below:

Here are two examples. With trapeziums you need to use the brackets keys on your calculator.

Kite A = ½ xy Trapezium A = ½(a + b)h

h

b

Where: x and y are the lengths of the diagonals.

Where: a, b = parallel side lengths h = perpendicular height

a

x

y

A = 3.1 m2 (1 d.p.)

A = ½ xy

= ½ × 3.9 × 1.6

Write the formula

Substitute x & y (or a, b & h)


A = 11 094 mm2

A = ½ (a + b) h

= ½ × (115 + 143) × 86

3.9 m

1.6 m

143 mm

115 mm

86 mm

Area of Kites and Trapeziums © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

Find the area of the trapezia below. Don�t forget square units. Eg. mm2, cm2, m2. Round to 1 d.p.

15 cm

11 cm

8 cm

A = ½ (a + b) h

= ½ × (11 + 15) × 8

A = 104 cm2

10

11

75 mm

48 mm

29 mm

12 8.6 m

2.2 m

11.8 m

15 cm

24 cm

12 c

m

A = ½ (a + b) h

A = ½ × (

A =

+ ) ×

9

15

13 93 cm

78 cm

54 c

m

14

28 m

41 m 53 m

14.7 m

7.7

m

9.6 m

27 cm

32 c

m

51 cm

16 45 cm

1.3 m

70 c

m

Answer in cm2

Find the area of these kites. Round to 1 d.p. if needed.

Example

Calc: 0 . 5 × ( 1 1 + 1 5 ) × 8 =

Example

45 cm

32 cm A = ½ xy

= ½ × 32 × 45

A = 720 cm2

Calc: 0 . 5 × 3 2 × 4 5 =

A = ½ xy

A = ½ ×

A =

×

1

22 cm

37 c

m

2

1.4

m

3.8 m

4

3

6

5

8

7

From Q.5 all units are in cm.

85 cm

27 cm

134

mm

206 mm

6

6 8

15 39.7

8.5

13.8

7

16 23

17.9

76.3

22.9

cm2

cm2

Area of Composite Shapes - Non Circular

Composite shapes are shapes that are made by combining one or more shapes. The area is found by either adding or subtracting the areas. The shapes involved are shown below.

The process for the sheet is to label the areas in the composite shape A1, A2 and so on. This may require the shape to have lines drawn inside it to break it up into the plane shapes. Below is an example. Find the area of the shape.

Square: A = l2

l

Rectangle: A = lb

l

b

Triangle A = ½bh

h

b

Rhombus A = ½ xy

x

y

Parallelogram A = bh

h

b

Trapezium A = ½(a + b)h

h

b

a

Kite: A = ½ xy

x

y

A = A1+A2 = 1 440 + 220

A1 = lb

A1 = 1 440 cm2

32 = × 45

A = 1 660 cm2

25 c

m

32 cm

45 c

m

54 cm

A1

25 c

m

32 cm

45 c

m

A2

54 cm

A1

25 c

m

32 cm 45

cm

A2

54 cm

20 cm

22 cm

A2 = ½bh

A2 = 220 cm2

= ½ × 22 × 20

Break the shape up and label the areas

Find missing lengths (in red)

Solve by finding individual areas

and then adding them.

Area of Composite Shapes - Non Circular © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

Composite areas are found by dividing the shape into two or more plane shapes, finding their areas then adding or subtracting them. Try these, round to 2 d.p.

1

A = A1+A2 = +

17 cm A1

A2

12 c

m 26

cm

13 cm A1 = lb

A1 = cm2

= ×

A = cm2

A2 = lb

A2 = cm2

= ×

2 A1 =

A1 = m2

=

A = A1 - A2 = -

A = m2

A2 =

A2 = m2

=

A1

A2 2.5 m

1.2

m

3

m 0.6

mm 42

75 mm 68 mm

mm 54

4

Find the shaded area.

18 c

m

cm 11

42 cm

5

3.7 m

4.1

m

5.3 m

m 1.2

6


7

A = A1 - 3A2 =

4.4 m

2.1

m

8

155

mm

62 mm

120 mm

172 mm

mm 103

mm 84

31 mm


mm 10

mm 10

Area of a Circle (Sheet 1)

The formula for calculating the area of a circle is:

A = r2 Where: A = Area of the circle, in the same units as the radius, but squared. (cm2, m2, mm2) r = The radius of the circle (distance from centre to circumference). Column 1 features circles with the radius shown. Use the area formula above to calculate the answer. The answer should be rounded to 2 decimal places and the units should be shown as square units. There is an example at the top of the column. Column 2 is the same as Column 1 except for one additional step. Instead of the radius you are given the diameter. So convert the diameter to a radius by dividing it by 2, write the radius in the space provided, either in or beside the circle. Then solve the questions the same way, but round to one decimal place this time. Column 3 starts with a mixture of questions that are either radius or diameter, so the questions are solved the same way as either Column 1 or Column 2. At the bottom of the column a circle is fit perfectly into a square, so the circle�s diameter is the same as the side length of the square. Calculate the square�s total area (as if the circle wasn�t there), then calculate the circle�s area. Then calculate the %Area that the circle accommodates within the square, by multiplying the fraction by 100. Did you expect the circle to take up more space, or less?


Area of a Circle (Sheet 1)

13

55 mm

14

17.8 cm

15

103 mm

16

0.8 m

19

Find the area to 1 d.p., watch for diameters.

Example

A = r2

= × 17.52

A = 962.1 mm2

35 mm

r = 17.5 mm

8

14.6 m

r =

9

9.8 km

r =

10

r =

11

83.7 m

r =

7

r =

77.2 cm

12

Example

A = r2

= × 242

A = 1 809.56 cm2

24 cm

Calculate the area of these circles, round to 2 decimal places.

1

17 mm

2

22.6 m

3

6.3 mm

4

33.7 cm

5

10.2 m

6

1.7 km

Calculate the radius then the area of these circles, round to 1 d.p.

= 35 cm

= d

r =

2.54

m

17

Find the area of the �..

31 cm

Square

A = l 2

18 Circle

Find ASQUARE

ACIRCLE as a percentage

Round to 1 d.p.

Area of Composite Shapes

A composite shape is a shape that is composed of two or more plane shapes. These two shapes can add together to create an area, or be subtracted. Before this sheet is attempted you should have completed earlier sheets on area of a circle. Column 1 are all exercises using addition. So calculate the individual areas and then add them together. The process is shown in question 1. Column 2 is essentially the same process, find the areas that make the shape but then subtract the areas. Question 8 will require Pythagoras Theorem to first be applied.

Area of Composite Shapes © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

Find the areas, sum for the total area. Round to 1 d.p. All lengths are cm.

1

A = A1 + A2 = +

A = cm2

9 A1 A2

A2 = l 2

2 =

A2 = cm2

A1 = ¼ r2

A1 = cm2 (1 dp)

= ¼ × × 2

2

9

A1

A2

14

A1 = ½ r2

A2 = lb

A = A1 + A2 = +

A =

3

A2 = ½bh

11

4

This time subtract the areas. Round to 1 d.p. All measurements in metres.

20

50 17

38

5

4.7

7.9

2.9

6

5.7

6.5

8

7

12

14

5 12

3

Volume - Find a Word

WORDLIST

RECTANGULAR

CYLINDRICAL

DIMENSIONS

TRAPEZOIDAL

TRIANGULAR

LENGTH

CONVEX

MILLILITRE

DIAMETER

CAPACITY

UNITS

CUBE

KILOLITRE

RADIUS

CUBIC

CYLINDER

VOLUME

AREA

CONCAVE

COMPOSITE

SQUARE

PRISM

UNIFORM

HEIGHT

SPACE

C I U E R A L U G N A T C E R

E C E X L A D I O Z E P A R T

A U I N Y N E S T I N U R D X

L B N V K I L O L I T R E X E

I X O C I C G T E A L S I A T

C C F O T O N Z A Z A K T I E

N E M O A E H G A A R O I E S

R L R V C X T H V L P N L M I

L L C U A A S E N O S S L E P

I L B L P R F I C I I I L T O

C R X E I Q E X C V X E M Y O

Y A A M C U E H O Z M N I R M

I P A C R A L U G N A I R T Y

C A S D R S X E R H O M B I C

D R N I L Y C Y L I N D E R L

Find the words in the puzzle from the wordlist.


PARALLEL FACES RHOMBIC

…………………………………………………………………………………………………………………………………. Copyright © mathsmentality.com.au 2014

Front, Side, Top and Back Views of 3D models Children investigate the various viewpoints of 3D objects. The 2D viewpoints (from the front, left side, right side, top and back) do not show depth on their own. Here’s an example. This 3D object ( made from eight cubes joined together ) can be drawn from different viewpoints as 2D images.

Front View Top View Right Side View Left Side View Back View

Children can construct their own 3D objects and then make 2D drawings of the different viewpoints. They can also construct a 3D object that matches the information given from a set of 2D viewpoints. Another idea is to match a series of 2D drawings with a particular 3D object from a selection of objects.

Left Right

Back

Front

Top


Name: …………………………………………………..…………………………………. Date:………………………………..

Front, Side, Top and Back Views of 3D models

Look at the front, right side, left side, top and back view drawings. Match each one with a 3D object. Circle the matching 3D object.

Front View Top View Right Side View Top View Right Side View Left Side View

Top View Right Side View Left Side View Back View Top View Left Side View

Front View Top View Right Side View Left Side View Back View Top View


Name: …………………………………………………..…………………………………. Date:………………………………..


Look at these 3D objects. Draw some of the 2D viewpoints ( from the front, right side, left side, top and back ).

Front View Top View Right Side View Top View Right Side View Left Side View

Top View Right Side View Back View Front View Top View Left Side View

Front View Top View Right Side View Left Side View Back View Top View


Name: …………………………………………………..…………………………………. Date:………………………………..


Look at these 2D viewpoints from the front, right side, left side, top and back. Collect some blocks and build a 3D object that matches the complete set of viewpoints. Check your model with your teacher.

Front Top Right Side Left side Back




DAMS & WATER SUPPLIES

Converting between Volume and Capacity

When you calculate the volume within a solid it's measured in cubic units such as mm3, cm3, or m3. These units are used usually to define empty space such as storage space, shipping containers or packaging, usually when they are to be filled with solid material. Capacity is measured in millilitres (mL), litres (L), kilolitres (kL) and Megalitres (ML). Each unit is 1 000 times larger than the unit before it. While capacity is usually associated with liquids it is also used with air. For example the space inside a car will have its capacity measured in litres. Column 1 starts with comparing mL and cm3. They are the same, so a measurement in mL, say 5.72 mL is the same in cm3, 5.72 cm3. So rewrite the number and change to the other unit. From question 7 you are asked to convert cm3 to L. As 1 cm3 is 1 mL, and there are 1 000 mL in a L, then 1 cm3 must be 1/1000 of a L. So divide by 1 000 or move the decimal point 3 places to the left to get your answer. Remember that litres is written with an upper case L. A common object where both capacity and volume are used is with car motors. The size of the engine could be given in c.c. (cubic centimetres) which is an accepted way of writing cm3, or litres (L). For example a 1 800 c.c. engine could also be described as a 1.8 L engine. Column 2 starts with the reverse, converting from L to cm3. This time you multiply by 1 000 or move the decimal point 3 places to the right. The last 6 questions involve the conversion between kL and m3. Just as with mL and cm3, they are identical so 1 kilolitre (1 000 L) = 1 cubic metre (m3). Just rewrite the number and change the unit. Column 3 asks you first to convert from m3 to L. Remember that 1m3 = 1 kL which is 1 000 L. So multiply by 1 000 or move the decimal point 3 places to the right. The next section of the column reverses the process, converting L to m3. Reverse the process by dividing by 1 000 or moving the decimal place 3 places to the left. This sheet doesn't deal with Megalitres (ML) as they are rarely used. But there are times when their use is essential when dealing with large capacities, can you think of where ML would be used?

Converting between Volume and Capacity

Change the units from mL to cm3 or the reverse

Example

73 mL 73 cm3 =

1 350 mL =

2 105 mL =

3 56.3 cm3 =

4 850 mL =

5 2.43 cm3 =

6 600 cm3 =

Convert these volumes in cm3 (c.c.) to litres

850 cm3 = 0.85 L 3 places left

7 1 000 cm3 =

8 800 cm3 =

9 450 cm3 =

10 2 100 cm3 =

11 1 700 cm3 =

12 750 cm3 =

13 1 250 cm3 =

14 5 000 cm3 =

15 85 cm3 =

16 4 302 cm3 =

17 120.4 cm3 =

18 333 cm3 =

19 2 006 cm3 =

20 500 cm3 =

21 25.1 cm3 =

22 1 007 cm3 =

23 10 cm3 =

Now reverse, change these from L to cm3

4.3 L = 4 300 cm3 3 places right

2 L = 24

0.5 L = 25

3.1 L = 26

0.2 L = 27

3.5 L = 28

29 1.75 L =

30 0.04 L =

31 4.03 L =

32 0.05 L =

33 0.01 L =

34 0.2063 L =

35 2.02 L =

36 0.25 L =

37 4.06 L =

38 0.96 L =

39 3.007 L =

40 4.55 L =

Change the units from kL to m3 or the reverse

Example

2.9 m3 2.9 kL =

41 7 m3 =

42 3.84 kL =

43 43 kL =

44 0.3 m3 =

45 204 m3 =

46 7.06 kL =

Change these volumes from m3 to litres.

2.53 m3 = 2 530 L 3 places right

7.2 m3 = 47

0.5 m3 = 48

3.7 m3 = 49

0.25 m3 = 50

16.403 m3 = 51

52 0.02 m3 =

53 5.62 m3 =

54 1.01 m3 =

55 7.9035 m3 =

56 18.006 m3 =

57 105.12 m3 =

Now change these from litres to cubic metres

2 650 L = 2.65 m3 3 places left

2 000 L = 58

1 700 L = 59

800 L = 60

3 075 L = 61

175 L = 62

63 422 L =

64 9.06 L =

65 45.6 L =

66 115 L =

67 2 L =

68 500.5 L =

69 3 000.6 L =


Units of Capacity

Capacity is another way of expressing volume. Rather than using length measurements, capacity is expressed using measurements normally associated with liquids. Usually mL, L and kL. This sheet deals with the changing of units between these three. As with length, (mm, m and km), capacity units are × 1 000 apart (cm is the exception with length). So you multiply by 1 000, or as hopefully you know, you move the decimal point 3 places to the right (multiplying) and to the left (dividing). Column 1 deals with changing from a smaller unit to a larger unit. With these you divide by 1 000. So move the decimal point 3 places to the left with these, remember to write the new unit after your answer, it will be the unit inside the brackets. Watch that you don't have unnecessary zeros in your answers when decimal points are involved. Column 2 is the reverse, this time moving to a smaller unit so you have more of them, so you are multiplying by 1 000. Move the decimal point 3 places to the right to make the number larger. Again remember to write the new units after the number. Column 3 asks you to find the volume of the prisms, the answer will be in cubic units, either cm3 or m3. Convert these to either mL (if cm3) or kL (if m3), rewrite the number and change the units. Then rewrite the answer in litres (L), using your skills from the previous 2 columns. Capacity is volume, so you still write 'V =' in your answer. Note that L is the symbol for litres, it is a capital letter, this may seem unusual but many metric units use capital letters, an example being �N� (Newtons, a measure of force) or �W� (Watt, a measure of electrical power).

Units of Capacity

Change these measure-ments to the larger units shown in the brackets

mL L ÷ 1 000 3 places left

L kL ÷ 1 000 3 places left

1 2 000 mL = [L]

2 5 000 L = [kL]

3 1 500 L = [kL]

4 3 400 mL = [L]

5 900 L = [kL]

6 500 mL = [L]

7 1 375 mL = [L]

8 250 mL = [L]

9 505 L = [kL]

10 50 L = [kL]

11 10 mL = [L]

12 35 mL = [L]

13 1 017 L = [kL]

14 110 mL = [L]

15 4 070 L = [kL]

16 1 400 mL = [L]

17 60 mL = [L]

18 15 L = [kL]

19 410 mL = [L]

20 5 030 L = [kL]

21 303 L = [kL]

22 1 L = [kL]

Convert the measurements to the smaller units shown in the brackets

kL L × 1 000 3 places right

L mL × 1 000 3 places right

23 1 L = [mL]

24 6 L = [mL]

35 0.871 kL = [L]

34 5.03 L = [mL]

32 3.05 kL = [L]

28 0.8 kL = [L]

40 0.003 kL = [L]

37 0.0025 L = [mL]

36 5.64 kL = [L]

39 0.07 L = [mL]

38 2.004 kL = [L]

27 0.75 L = [mL]

26 1.25 L = [mL]

33 0.079 L = [mL]

31 1.12 kL = [L]

30 0.01 kL = [L]

29 3.2 L = [mL]

25 4.5 kL = [L]

41 0.0005 kL = [L]

42 1.9 L = [mL]

43 0.0087 kL = [L]

44 0.053 L = [mL]

Calculate the volume in either cm3 or m3, write the answer as mL or kL, then rewrite converting to litres

46

5 m

15 m

2 m

kL

L

45

4 cm

10 cm

5 cm

V = lbh

=

cm3 V =

mL V =

L V =

47

5 cm 20 cm

8 cm

48

3 m

10 m

2 m


Volume and Capacity

This sheet involves both volume units (mm3, cm3 and m3) and capacity units (mL, L and kL). Column 1 starts with solids built from cube blocks. Each cube is 10 cm3 in volume. As 1 cm3 is equal to 1 mL, that also means that each block has a capacity of 10mL. So count the blocks and multiply by 10 for the volume and capacity. The second part of the column gives you the area of the face of the prism and its height. Use V = Ah to find the volume. After you find the volume convert the cm3 volume to mL and the m3 volumes to kL. Column 2 involves finding the volumes for cubes and rectangular prisms. To change the units remember that: Column 3 deals with triangular prisms and cylinders. The formulae to use for these is: Remember to watch for when you are given a diameter rather than a radius. Halve the diameter (÷2) to get the radius, then use the radius in the formula.

Volume of a Rectangular Prism: V = lbh

Volume of a Cube: V = l 3

1 cm3 = 1 mL

1 m3 = 1 kL

Volume of a Triangular Prism: V = ½lbh

Volume of a Cylinder: V = r2h

Volume and Capacity © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

Find the volume of these solids then rewrite in mL. Each cube has a volume of 10 cm3.

2.6

m

4.4 m2

1 V = cm3

Capacity = mL

2

V = Capacity =

3

V =

Capacity =

Use V = AH to find the volume of these solids. Then convert m3 to kL or cm3 to mL.

4

9 cm

Area 115 cm2

= ×

V =

V = Ah

Capacity =

5 11 m

57 m2

6

If these solids were immersed in water, what volume of water would be displaced? To 1 d.p.

V =

=

V =

7 Cube

9 cm

Capacity =

8

7.2

m

2 m

3 m

12

9 cm 12 cm 16

cm

9

12 cm

18 cm

10

11

8.3 m

Cube 14.2 cm

3.6

m

5.4 m

14

13

16

15

17

3.2 m

4.1 m

10.6

m

15.2 cm

27.6

cm

5 m

3.9 m 4.5 m

3.7 m

25 cm

22 c

m

16 cm

Centicube Volumes

Volume is a measure of the amount of space an object occupies. The units used in measuring volume are cubic units: mm3, cm3 and m3. The solids on this sheet are all constructed from centicubes (each 1 cm3). This allows the volume to be found by counting the cubes with the volume being the total number of cubes (in cm3). The first 2 columns ask you to count the cubes, you have to accept that the cubes that you can't see, due to cubes being in front, are still there. A cube must be on top of another cube to be above the first layer. When you write the volume you must include the units (cm3). Column 3 introduces the Volume formula : V = Ah. This applies to any shape with a uniform cross-section, (this means the blue area is the same throughout the height of the shape). Count the number of squares that make up the blue area (A) and multiply this by the number of red squares that make up the height (h), this will give you the volume in cm3. Don't let the word 'height' confuse you. You may feel that height must go up and down but the word height is used to describe the direction of the uniform cross-section. When you think about it if you turn the page sideways it will be up and down, so the answer will be the same.

Centicube Volumes

1

V =

13

V =

14

15

16

18

17

19

21 Face Area (A) = cm2

Shape height (h) = cm

A × h = cm3

23 A = h =

V = Ah =

22 A = cm2 h = cm

V = Ah = cm3

24 A = h =

V = Ah =

25 A = h =

V = Ah =

2

V = cm3 V = cm3

3 4

V =

V =

5 6

V =

V =

7

V =

8

V =

9

V =

10

V =

11

V =

12

V =

V =

V =

V =

V =

V =

20

V =

Calculate the volume of these solids built from identical cubes, assume 1 cube = 1cm3.

Find the area of the front face then multiply it by the height (the distance the shape goes back into the page).


Volume, Area and Height - Volume of a Prism

When a solid has a uniform cross section (same shape throughout the height of the solid) then it is a prism. The formula V = Ah can be used to obtain the volume of the solid. The area will be given in square units (mm2, cm2, m2) and the height of the solid will be given in mm, cm and m. Multiply the two together to get your answer. The answers will be in cubic units mm3, cm3, m3. The first columns uses the same method as shown in the example below, this is: writing the formula (V = Ah), substituting the values (for A and h), with an '=' sign before them and a '×' sign between them, then the answer with the appropriate cubic units after it. Example Column 2 is the same as column 1 except that the height unit doesn�t match the area unit. So you need to change the height to same units as the area. Then solve as before. Column 3 applies your skills to a duck pond, the ducks are getting their bills all muddy when they dive down, it�s time to give them a little more depth.

7 cm

55 cm2

V = Ah

= 55 × 7

V = 385 cm3 Volume is measured in cubic units


Volume, Area and Height - Volume of a Prism

13 m

17 m 2

0.8 cm

2.25 cm2

2.2

cm 70.5 mm2

61 c

m

8.7 m2

19 m

m

61 m

m2

Multiply the area by the height to find the volume

83 cm 2

53 c

m

4

35 mm2

14.7 mm

1

12 m2

3 m

2

9 cm 26 cm2

V = Ah

= ×

V = m3

3

5

6

7 107 mm2

41 m

m

8

9

13 cm

56 cm2

Change the height unit to match the area units. Then multiply for the volume. Round to 2 d.p.

10

11

12

82 mm

120 cm2

13

106 cm

9.6 m2

95 cm2

0.17 m 14

15

16

17

Apply your volume skills to these questions. The bill for this job is too much to wear!

A council duck pond has to have the mud build-up removed. It has to be drained, excavated and refilled.

46.6 m2 35 cm

23 cm

18 Find the mud volume in m3.

19 Find the water volume in m3.

20 Mud excavation/removal costs $712 per m3 (or part m3).

21 Find the volume of water in the mud cleared pond in m3.

MUD

WATER

22 Find the percentage increase for the volume of water. (1 d.p)

% Increase = H2O VolNEW

H2O VolOLD × 100 - 100

=

× 100 - 100

% Increase =

315 mm2

0.2

m

14.6

cm

1.8 m2

6 400

0.08

m mm2

Find the cost for mud removal.

Volume of Triangular Prisms

There are two ways of calculating the volume of a triangular prism. You can calculate the Triangular face area and multiply by the height of the solid, or you can treat the prism as being half of a rectangular prism of the same size.

The second method finds the answer in one step so it is quicker. But the first method is essential to learn as it is a method that will be used regularly with prisms. Column 1 starts with a reminder about the method of finding the area of a triangle. The remainder of the column is using the above left method. It may be that you prefer the second method, but apply the area then volume process regardless, it is a skill you will need. Column 2 is the method shown above right. So it is quicker as it is solved using one formula/substitution. Column 3 can be solved using either method and are worded questions. Watch that all units are the same when finding the volume.

Area then Volume Method

A = ½bh

=

A = 48 cm2

½ × 12 × 8

Example

This is area so it is measured in square units

A = ½bh then V = Ah 8

cm

12 cm 6 cm

V = Ah

=

V = 288 cm3

48 × 6

This is volume so it is measured in

cubic units

V = ½lbh

=

V = 288 m3

½ × 8 × 12 × 6

Volume Method

Example

V = ½lbh

8 cm

12 cm 6 cm


cubic units

Volume of Triangular Prisms © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

Find the volume using 2 steps, find Area first, using A=½bh, then the Volume using V = Ah.

Use A=½bh to find the area of these triangles.

1

19 cm

24 c

m

A = ½bh

= ½ × ×

2

A =

A = 1.8 m

2.4

m

3

31 mm

57 m

m

4

12 c

m

17 cm 8 cm

V = Ah

=

A = ½bh

cm3

5

2.7 m

6

5.3

m

3.2 m

120 mm 105 mm 75

mm

× 8

cm2

A triangular prism is half of a rectangular Prism. So use V=½lbh to find the volume.

V = ½lbh

V = cm3

= ½× × ×

7

15 cm

14 c

m

9 cm

8

24 mm 13 mm 37

mm

9

1.8 m

2.9

m

1.1 m

10

11

15 cm

24 c

m

17 c

m

12

13

7.2 m

8.5

m

5 m

42 cm

63 cm

54 c

m

32 cm

40 c

m

26 cm

Now apply your skills to these questions.

14 Jane is burying a drainage pipe in her yard. Find the volume of soil to be removed (in m3).

0.6 m

1.7 m

15 A mining company has a coal pile between two retaining walls. Find the volume in m3.

16 If the coal has a density of 845 kg/m3. Find the mass of the coal in T. (1 T = 1 000 kg).

35 m

16 m

22 m

17 A steel cow-feeding trough, is shown below, find its volume in m3 to 2 d.p.

95 cm

65 c

m

3.9 m

A = cm2

4 2 = 1 9 0 5 .

Volume of Various Prisms

Finding the volume of a prism is found by finding the area of the uniform cross section and multiplying it by the height of the solid. This sheet deals with non-circular prisms. The face that requires the area calculation is always the front face with this sheet, the formula used will be one of the following:

Triangle h A = ½bh

b

Rhombus A = ½xy y

x

Kite A = ½xy

y

x

Parallelogram A = bh

b

h

Trapezium A = ½ (a + b) h

a

b

h

a

b

h

Cubes V = l 3

Rectangular Prisms V = lbh

L

L

B

H

Cubes, rectangular prisms and triangular prisms can be solved using their specific formulae. However the other solids require you to first calculate the area of the front face then use this answer to find the volume. An example for a trapezoidal prism (prism with a trapezium as its uniform cross section) is shown below. Example - Find the volume.

14.2 m

9.6 m

8.5 m

16 m

A = ½ (a + b) × h

A = 101.15 m2

= ½ × (9.6 + 14.2) × 8.5

This is the area of the front face so it is

measured in square units.

V = Ah

=

V = 1 618.4 m3

101.15 × 16


cubic units

Volume of Various Prisms © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

These shapes will often require you to find the face area first, then use V = Ah for the volume. Round to 2 d.p. when needed.

1 Cube

16 cm

2

42 cm

25 c

m

58 cm

3

1.05 m

76 cm

56 cm

4

18

38

24

30

Units are in mm.

9

6

1.4 m

48 c

m

57 cm

7 32 mm

36 m

m

52 mm 13

mm

V in cm3.

11

V in m3.

10

4.2 m

3.8

m

2.6

m

5.4 m

5 Cube

22 mm

8

32 cm

73 cm

1.33

m

V in cm3.

3.9 m 5.2 m

4.1 m

12 V in m3.

13

7.4 m 9.2

m

2.9 m

V in cm3

65 cm 1.8 m

52 cm

95 cm

2.6

m

78 cm

Volume of Cylinders

The standard formula for a prism is V = Ah. Where: V = the volume of the prism A = the uniform cross sectional area h = the height of the prism But with cylinders the cross sectional area is a circle, which has an area of r2. So if you replace A with r2 you have:

The formula for a cylinder is V = r2h. Where: V = the volume of the prism r = the radius of the circular face h = the height of the cylinder Column 1 starts with an example showing the formula line, substitution and then answer. Make sure you show cubic units. Eg. mm3, cm3 and m3. Column 2 has an extra step, you are given the diameter of the circle. So before you start, divide the diameter by 2 to get the radius and then use the formula as you did in column 1. Column 3 applies what you have learned to some worded problems. There is also a table at the bottom of the column, no working required, just answers. Below is an example of finding the volume when given the cylinder height and diameter. Example - Find the volume to 1 decimal place.

V = 209 956.6 cm3

V = r2h

= × 42.52 × 37

85 cm

r = 42.5 cm

37 cm

85 ÷ 2 = 42.5

Write the formula

Substitute r and h

Solve showing cubic units

Volume of Cylinders © FREEFALL MATHEMATICS - FREEFALL MATHEMATICS ALTITUDE BOOK 2 - LICENSED FOR NON-COMMERCIAL USE

Find the volume of these cylinders using the key. Round to 1 decimal place.

Example

= × 32 × 10

V = 282.7 cm3

V = r2h

units3 must match

3 cm

10 c

m

1

V = cm3

V = r2h

5 cm

8 cm

2

V = r2h

2 m

7.7

m

5

6

4 11 cm

53 c

m

3

26 mm

42 m

m

1.6

m

0.8 m

34 mm

57 m

m

Careful! Diameters in use. Divide by 2 first for the radius. Answer to 2 d.p.

6

V = m2

V = r2h

= × 3 m

2.2 m

r =

× 3 2

7

8

10

11

12

13

12 c

m 28 cm

r = 63 mm

85 m

m

r =

r =

55 cm

62 cm

r = 4.3 m

4.1

m

r =

d = 87 mm h = 15 mm

r =

1.9 m

2.5

m

Calculate the volume of concrete in the cylindrical pylon below to 2 d.p. Calculate its weight (W) given the concrete weighs 2.4 T/m3.

14 V =

W =

0.3 m

9.6

m

Solve these problems involving cylinders.

The glass below contains 45 cm3 of HCL acid. If water is added to fill the glass find, to 1 decimal place, the:

15

11 c

m

6 cm

Volume of the empty glass (cm3).

16 Percentage of acid in the full glass.

Complete the table, which is in cm. Find the volume to the nearest cm3.

17

Q.

d

18

19

20

21

22

17

106

82

45

65

33

Volum

e (cm3)

r h

25

75

20

55

27

85

Acid

Water Added

9 74 cm

168

cm

r =

Finding Area and Volume - Composite Shapes

The volume of a prism is found using the formula V = Ah. So if you know how to find the area, you only have to multiply by the height to get the volume. This sheet has two columns, the left column are questions finding the area. The right column are questions finding the volume. But the columns are related because the questions match in layout, for example, Question 1 is a composite shape made from two rectangles, Question 5 is a composite solid made from two rectangular prisms. The method of solving is exactly the same in both questions, the only difference is the extra step in finding the volume. Below is an example. Example - Find the volume of the shape below.

Here is the solid, find its volume.

14 m

25 m

11 m

42 m

28 m

Break the front face up into two rectangles. Label the rectangles A1 and A2.

14 m

25 m

11 m

42 m

28 m

A1

A2

Calculate the two separate areas. As this is area, the units are square units.

A1 = lb A2 = lb

= 11 × 42

A1 = 462 m2

= 14 × 25

A2 = 350 m2

Add the two areas to get the total area of the front face. A = A1 + A2 = 462 + 350 = 812 m2

Multiply the area by the height to get the volume. Volume is in cubic units. V = Ah = 812 × 28 = 22 736 m3

Finding Area and Volume - Composite Shapes

A1 =

A2 =

V = Ah =

16 cm

18 cm

45 cm

68 c

m

1

Calculate the area of these shapes by breaking them up into parts first. All angles are right angles, remember to use square units, e.g. cm2.

A1 = lb

A2 =

A1 =

×

cm2

A2 = lb

A2 =

A2 =

×

cm2

A = A1 + A2 = cm2 + =

A1

A2

2 A1 =

A2

A1 =

A2 =

A2 =

3

A1

A2

A2

A2

7 cm 11 cm

A2 A1

135 m

90 m

170

m

110

m

Find the shaded area

4

A2

A2

8 cm

4 cm 10 cm

A1 A2 A3

Round to 2 d.p.

A2

A = A1 + A2 + A3

= + +

A =

Now apply your skills to find the volume. Use the same method as in the left column, except add one more line V=Ah to find the volume.

5

2.8 m

3.5 m

1.8

m

1.4 m

7 m

A = A1 + A2 = m2 + =

m3 × 2.8 =

6

44 cm 17 cm 32 cm

26 c

m

35 c

m

7

9 cm

26 cm

12 c

m

8

21 c

m

14 cm 9 cm


A = A1 - A2 = m2 = -

Shaded area, to 2 d.p.

A = A1 - A2 = = -

A1 =

A2 =

V = Ah =

A = A1 - A2 =

cm2

Solve: 1. m + 3 = 10 11. 3a = 18 21. m + 12 = 12 31. 8m = 5 2 ...

Documents

Transcript of Solve: 1. m + 3 = 10 11. 3a = 18 21. m + 12 = 12 31. 8m = 5 2 ...