Diferensiasi numerik
-
Upload
afifah-nurul-maulina -
Category
Documents
-
view
802 -
download
158
description
Transcript of Diferensiasi numerik
DAFTAR ISI
DAFTAR ISI1BAB I PENDAHULUAN2Latar Belakang2Tujuan2Manfaat3BAB II PEMBAHASAN4Dasar Teori4Permasalahan dan Pembahasannya7Soal7Jawaban dan Pembahasannya8BAB III PENUTUP11DAFTAR PUSTAKA12
BAB I PENDAHULUAN
1.1 Latar BelakangDiferensiasi Numerik merupakan salah satu metode yang penting dalam ilmu komputasi. Persoalan perhitungan turunan fungsi cukup banyak muncul dalam bidang rekayasa, misalnya dalam bidang pengolahan citra (image processing), turunan fungsi diterapkan untuk mendeteksi sisi (edge) obyek pada suatu citra. Sementara dalam perhitungan numerik sendiri, turunan fungsi dalam orde yang lebih tinggi, f ', f ", f "', ..., kadang-kadang diperlukan. Misalnya untuk menghitung batas-batas galat interpolasi polinom atau untuk menghitung galat integrasi numerik dengan aturan trapesium.Bila persamaan fungsi f(x) diberikan secara eksplisit, maka kita dapat menentukan fungsi turunannya, f'(x), f"(x), ..., f(n+1)(x), lalu menggunakannya untuk menghitung nilai turunan fungsi di x = t. Seringkali fungsi f(x) tidak diketahui secara eksplisit, tetapi hanya diketahui memiliki beberapa titik data saja. Pada kasus seperti ini kita tidak dapat menemukan nilai turunan fungsi secara analitik. Sebaliknya, pada kasus lain, meskipun f(x) diketahui secara eksplisit tetapi bentuknya rumit sehingga menentukan fungsi turunannya merupakan pekerjaan yang tidak mangkus dan tidak praktis.Untuk kedua kasus terakhir, perhitungan nilai turunan dapat dikerjakan secara numerik (numerical differentiation atau numerical derivative). Nilai turunan yang diperoleh merupakan nilai hampiran. Sebagaimana halnya pada integrasi numerik, perhitungan turunan numerik juga menggunakan nilai-nilai diskrit. Maka, fungsi dalam bentuk tabel merupakan bentuk alami untuk perhitungan turunan.Oleh karena itu saya membuat Laporan Akhir Praktikum Fisika Komputasi menggunakan pembahasan Diferensiasi Numerik karena metode ini dirasa mampu menyelesaikan persoalan yang fungsi f(x)-nya tidak diketahui secara eksplisit.1.2 TujuanTujuan dari dilaksanakannya praktikum Fisika Komputasi adalah diharapakan praktikan dapat memahami dan menjelaskan prinsip kerja software MatLab, dapat mengolah data dengan software MatLab, serta dapat mengerjakan persoalan fisika menggunakan perhitungan numerik dan melakukan pemodelan dengan software MatLab.1.3 Manfaat1.3.1 Praktikan dapat memahami dan menjelaskan prinsip kerja software MatLab.1.3.2 Praktikan dapat mengolah data dengan software MatLab1.3.3 Praktikan dapat mengerjakan persoalan fisika menggunakan perhitungan numerik dan melakukan pemodelan dengan software MatLab.
BAB IIPEMBAHASAN
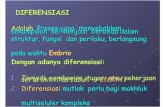
2.1Dasar TeoriPersoalan turunan numerik ialah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Meskipun metode numerik untuk menghitung turunan fungsi tersedia, tetapi perhitungan turunan sedapat mungkin dihindari. Alasannya, nilai turunan numerik umumnya kurang teliti dibandingkan dengan nilai fungsinya. Dalam kenyataannya, turunan adalah limit dari hasil bagi selisih: yaitu pengurangan dua buah nilai yang besar (f(x+h) - f(x)) dan membaginya dengan bilangan yang kecil (h). Pembagian ini dapat menghasilkan turunan dengan galat yang besar. Lagi pula, jika fungsi f dihampiri oleh polinom interpolasi p, selisih nilai fungsi mungkin kecil tetapi turunannya boleh jadi sangat berbeda dengan nilai turunan sejatinya. Hal ini masuk akal sebab turunan numerik bersifat "halus", dan ini berlawanan dengan integrasi numerik, yang tidak banyak dipengaruhi oleh ketidaktelitian nilai fungsi, karena integrasi pada dasarnya adalah proses penghalusan. (Anonymous, 2012)Misal diberikan nilai-nilai x di x0-h, x0, dan x0+ h, serta nilai fungsi untuk nilai-nilai x tersebut. Titik-titik yang diperoleh adalah (x-1, f-1), (x0, f0), dan (x1, f1), yang dalam hal ini x-1= x0-h dan x1= x0+h. Terdapat tiga pendekatan dalam menghitung nilai f(x0):1. Hampiran selisih-maju (forward difference approximation)f(x0) = = 2. Hampiran selisih-mundur (backward difference approximation)f(x0) = = 3. Hampiran selisih-pusat (central difference approximation)f(x0) = = Tafsiran geometri dari ketiga pendekatan di atas diperlihatkan pada Gambar 2.1
backward difference approximationforward difference approximation
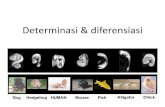
central difference approximation
Gambar 2.1 Tiga pendekatan dalam perhitungan turunan numeric
backward difference approximationbackward difference approximationRumus-rumus turunan numerik untuk ketiga pendekatan tersebut dapat diturunkan dengan dua cara, yaitu: 1. Dengan bantuan deret Taylor 2. Dengan hampiran polinom interpolasi Kedua cara tersebut menghasilkan rumus yang samaMisalkan diberikan titik-titik (xi, fi) , i = 0, 1, 2, ..., n, yang dalam hal ini xi = x0 + ih dan fi = f(xi). Jika kita ingin menghitung f'(x), yang dalam hal ini x = x0+sh, s R dengan ketiga pendekatan yang disebutkan di atas (maju, mundur, pusat), maka
1. Hampiran selisih-maju
2. Hampiran selisih-mundur
3. Hampiran selisih-pusat
Perhatikan, bahwa hampiran selisih-pusat lebih baik daripada dua hampiran sebelumnya, sebab orde galatnya adalah O(h2).
2.2Permasalahan dan Pembahasannya2.2.1 Soal:Sebuah mobil bergerak beraturan dengan kecepatan v tercatat di berbagai titik sepanjang jarak x sebagai berikut:t (s)048121620
v (m/s)0246810
Tentukan percepatan mobil dengan menggunakan pendekatan numerik! Serta bandingkan hasilnya dengan perhitungan secara analitik!2.2.2 Jawaban dan Pembahasannya:1. Secara NumerikSoal ini dapat diselesaikan dengan menggunakan metode diferensiasi numerik. Dalam metode ini terdapat tiga macam pendekatan, yaitu forward modeling, backward modeling dan central modeling. Sedangkan pada laporan akhir ini saya menggunakan pendekatan forward modeling.Berikut pseudocode untuk metode diferensiasi numerik:
set xset f(x)i, i=0..nfor i=1 to n dobd(x)i=[f(x)i-f(x)i-1]/xend for
Pseudocode tersebut diimplementasikan pada software MatLab. Kode program dijalankan pada command window dengan sebelumnya dituliskan dalam fungsi script. Berikut implementasi kode program yang dituliskan pada fungsi script:
Pada kode program n berisikan nilai banyaknya data t; sedangkan f berisikan data v atau kecepatan mobil. Lalu ada perintah i=1:n-1, i adalah bilangan yang difungsikan dan masuk dalam perhitungan. Kemudian terdapat fungsi dari forward difference yaitu fd(i)=(f(i+1)-f(i))/dt. Setelah difungsikan, dalam kode program hasil perhitungan akan ditampilkan dalam command window dengan nama Hasil..Berkut hasil perhitungan yang telah dihitung dengan software MatLab:
Dari perhitungan yang telah dilakukan menggunakan software MatLab diketahui bahwa untuk detik ke 0,00; 4,00; 8,00; 12,00; 16,00; dan 20,00 percepatan mobil adalah 0,500 m/s2.2. Secara AnalitikSetelah dilakukan perhitungan secara numerik, saya melakukan perhitungan secara analitik untuk membandingkan hasil perhitungan. Seperti yang telah diketahui bahwa rumus untuk menghitung besarnya suatu percepatan benda bergerak lurus beraturan adalah:
(Romo, 2010)
Diketahui:Vt = 10; = 20 = 0,5 m/s2.Hasil perhitungan secara numerik maupun secara analitik berhasil sama yaitu 0,5 m/s2.Kemudian bila diplot pada Ms. Excel, didapatkan hasil grafik seperti ini:
Garis lurus pada hasil grafik adalah menunjukkan bahwa gerak yang dijalankan oleh mobil benar merupakan garak lurus beraturan, hal itu dikarenakan nilai trend antara kecepatan dan tiap waktunya memiliki jarak yang selalu sama.
BAB IIIPENUTUP
Kesimpulan yang dapat diambil dari laporan akhir ini adalah dalam fisika, penurunan problem diferensiasi numerik dapat menggunakan metode finite difference. Metode ini terdiri dari pendekatan selisih maju (forward difference), selisih mundur (backward difference) dan selisih pusat (central difference). Pendekatan selisih pusat memiliki nilai hasil yang lebih baik daripada dua pendekatan lainnya karena memiliki nilai error yang lebih kecil.Dalam laporan ini saya membandingkan hasil perhitungan secara numeric dan analitik, keduanya memiliki hasil yang sama yaitu 0,500 m/s2. Tidak hanya itu, saya juga mem-plot pada software Microsoft Excel untu membuktikan bahwa gerak yang dijalankan oleh mobil pada permasalahan adalah benar Gerak Lurus Beraturan.
DAFTAR PUSTAKA
Anonymous. (2012). Retrieved January 2014, from http://informatika.stei.itb.ac.id/rinaldi.munir/Buku.pdfRomo, I. (2010). Kinematika. Jurnal Fisika .
Laporan AkhirPraktikum Fisika Komputasi1