THE MAXIMUM CAPTURE PROBLEM INCLUDING RELOCATION

THE MAXIMUM CAPTURE PROBLEM INCLUDING RELOCATION^CHARLES REVELLE, DANIEL SERRA

Department of Geography and Environmental Engineering, The Johns Hopkins UniversityBaltimore, MD 21218, USA.

ABSTRACT

In an earlier work on facility siting in a competitive environment it was shown how to site/) newfacilities in such a way as to maximise market population captured from competitors. In this work amore complicated but more realistic problem is formulated — how to site a limited number of newfacilities and relocate a specified number of old facilities — to meiximise the market share captured.Relocation is an important component of competitive facility siting because the entrance of com-petitors after the initial siting of outlets causes a change in the marketing landscape. Computationalexperience with this zero-one linear programming problem is provided in the conte5ct of the classiceconomic market strategies suggested by Coumot and Stackelberg.

RESUME

Dans un article precedent concemant l'emplacement des installations, nous avons examine com-ment P nouvelles installations pouvaient etre localisees de f agon a maximiser la population prise auxconcurrents. Cet article vise a formuler un probleme plus complexe mais davantage realiste — com-ment determiner un emplacement pour un nombre limite de nouvelles installations et relocaliser unnombre specifique d'anciennes installations — en maximisant la prise de part de marche. La relo-calisation est une composante essentielle de l'emplacement des installations competitives puisquel'arrivee de concurrents, apres la localisation initiale, induit une modification dans l'environnementcommercial. Nous foumissons une estimation de ce modele de programmation lineaire en nombresentiers (zero — un) dans le contexte des strategies de marche de l'economie classique suggereespar Cournot et Stackelberg.

1. INTRODUCTION

Hotteling [1] (1929) first studied the issue of market capture by the siting of competitive servers.He showed that the optimal location of two profit maximizing icecream vendors in a beach is backto back rather than one at the one quarter mark and one at three fourths mark of the beach. Thisapparently simple finding gave rise to extended discussions about the practicalify of the result whensome of the assumptions were relaxed. In the relatively recent past, Teitz [2] (1968) showed thatthe extension to a three vendors case would no longer lead to an equilibrium. Eiselt and Laporte[3] [4] (1987) considered the location of a new facilify in a finite linear market with n vendors. Theyassumed that (1) customers are uniformely distributed along the line, (2) the attraction to a facilifyis directly proportional to the size of the facilify and (3) that attraction is inversely proportional tothe distance separating customers from the facilify. As Dobson and Karmarkar [5] (1987) note, mostof these models while they serve the economist's purpose of understanding the basic mechanismof equilibrium, do not resolve the decision problem faced by an actual retailer in a competitivesituation.

Hakimi [6] (1981) extended the hotelling problem to two dimensions, studying the location of nnew servers in a network with;? already existing ones. ReVelle [7] (1986) casts this np-hard problemas a linear integer program in which the objective of the entering firm is to maximize the populationcaptured by the siting of its servers, where customers are assumed to attach to the closest server.

In this paper we present first an extended formulation of ReVelle's maximum capture problemwhich allows the siting of new servers and the relocation of any number of existing servers in orderto capture the maximum market demand from already sited competitors. In the second part ofthe paper computational experience with the formulation is offered. The third section applies themodel to location strategies in a duopolistic framework. Observations on the model and furtherresearch conclude the paper.

* Reed. Dec. 1988 Revd. Nov. 1989 Ace. Nov. 1989 INFOR vol. 29, no. 2, May 1991

130

THE MAXIMUM CAPTURE PROBLEM 131

2. THE MAXIMUM CAPTURE PROBLEM INCLUDING THE

RELOCATION OF EXISTING FACILITIES (MAXRELOC)

Suppose we are in a situation in which a firm A is already established in the marketplace vdthr servers distributed on the network. Although competitors are also spatially dispersed on thenetwork, firm^l wishes to expand its presence and to improve the location of some of its currentservers. In order to improve its competitive position, GimA is considering the relocation of J of its rexisting servers, and the opening ofp new facilities. In this formulation, we must be careful to countin the objective not only the population captured by the new facilities and the relocated facilitiesbut also take care to subtract from the objective that population lost to competitors when serversof firm A abandon their previous sites for new positions. The criterion becxjmes maximum netcapture where gains are attributed to placement of the new facilities and losses to the relocation ofthe old ones. In that sense, the objective follows the formulation of the Maximal location CoveringProblem of Church and ReVelle [8] (1974).

Some assumptions need to be made explicit in order to justify this objective function. First, thefacilities are generic in the sense that the facilities could be of any type, from banks to retail shops tofast food restaurants. This forces us to treat the demand for the use/consumption of these servicesas general and tractable as possible. In this sense, we will assume that both competing firms havethe same demand structure so that the consumer/user ofthese is indifferent when having to choosebetween the consumption/use of both firms' goods/services, ceteris paribus. So only product/servicedifferentiation mil occur when the servers are located at different distances from the consumer;that is, we will assume that consumers always travel to their closest facilify to obtain the desiredproduct, or are supplied by their closest server. Firms are assumed to have the same unit costs, andrelocation costs are disregarded, although it is relatively simple to make them explicit.

In any pattem of siting it is possible that some population might have Iwo or more nearestservers, that is, two or more servers at the same distance from that population. Sueh a situationis most likely to occur when firms co-loeate on top of each other, thus captui ing the same nodes.From a practical standpoint, this scenario could occur when the locational strategy of a firm is tolocate close to its competitor, as the second ice-cream vendor did. In this case, we will assume thatif a demand node has tsvo competing facilities located at the same distance from it, each server willcapture half of the population covered.

The mathematical formulation of the problem is as follows:

ieic ieio leic ieiA ieio

Subject to:

E ^'e^co (1)

ieIC (2)

Zi +3',- < 1 ieIC (3)

+ V,- > 1 - ^Xj ielA (4)

> 1 - E^y - E^i '^^o (5)

(6)

132 C. REVELLE AND D. SERRA

= ^ + * (7)

y i , Z i , V i , q i , X j = 0,1 i e I , j e J ( 8 )

where:

/ the set of demand nodes that are available for capture {i is the index of demand nodes);IA Set of nodes covered exclusively by firm A at the start;IC Set of nodes covered exclusively by firm Cat the start;IO Set of nodes covered by both firms^ and C at the start;

IAO IAUIOICO ICUIO

J the set of eligible facilify sites (j is the index of available facilify sites);JOC the set of sites currently occupied by competitors;JNO the set of sites not currently occupied which are eligible to have servers deployed at them;

Si the distance from node / to the closest competitor firm;dij shortest distance (time) between node / and site;;Ni = ij e J\dij < Si} the set of available facilify sites that are strictly closer to node i than to

its current closest C firm is to / (competitor);Ki = {/' ei\dij = Si} the set of the sites which are precisely at the distance S, from node /;yi 1, 0; 1 if node i, i in ICO, gets a new server within S,; that is, some server is closer to i than

its previous closest server;Xj 1,0; 1 if a facilify is sited at;;Zi 1,0; 1 if node / is captured by a server sited within X,; that is, at the currently closest server

to i or at a site whose distance from i is equal to S,; viz., Zi is one if / is captured but doublyserved;

V, 1, 0; 1 if node i, previously in the sphere of ̂ 4, is captured by a competitor by virtue of therelocation;

qi 1, 0; 1 if node i is "half" lost to a competitor; i.e.,ii by virtue of the relocation, node i isserved by two servers located at a same distance;

ai the population at node j .

As mentioned before, the objective takes into account the nodes lost to competitors. Variables v,and qi represent, when equal to one in the solution, the nodes lost and half lost to competitors. Theobjective will try to minimize this loss of population.

The value of 5/ which defines the sets Ni and Kt must be chosen carefully. Consider the oc-cupied facilify sites around i. Note that the closest server to i {i in IA) is not a competitor firmby definition of Ni. That is, the closest server is a member of firm^l. If the second closest serverto node / is a competitor, then 5,- is the set equal to the distance from i to the nearest competitorfacilify. If the second closest server to i is a member of firm^, and the third closest is a competitorthen 5, is set equal to the distance to the competitor, and so on. It is observed that N consists ofeligible sites which are strictly closer than the closest competitor.

The first group of constraints say that no demand node which is currently fully or partiallyserved by the competition is captured by firm^ unless at least one the servers of^ is placed at asite closer to i than its current closest server (which is the competitor C).

The second set of constraints state that a demand node which is currently served by the com-petitor firm C only can be doubly served (z, = 1) by^ and C if an^ server is positioned at a nodewhose distance to the demand node equals the distance from the demand node to the competitor.In this case the coefficient in the objective for z, is equal to the population divided by two, sincenode i is served by both servers.

Constraint group three makes infeasible both half capture and complete capture of node i.Note that in this case since we are maximizing, node / will be taken as fully captured rather thanhalf captured if it should occur that both^ is closer to i than C was and &nA server is at the same


distance from / as C was. If both conditions obtain, node / will be fully captured because full captureimproves the objective more.

Observe that even though the variablej,- is defined as equal to one if the node / is fully capturedby firm^, it can happen that in realify the population served has only increased by half. This occurswhen node i was doubly served prior to the relocation. If after the relocation, firm>l locates one ofits servers closer to i than its former server, the node would be fully captured, but the increase inthe population captured is half.

The fourth group of constraints says that the population at i is either lost (v, = 1) or halflost {qi = 1) to a competitor if there is no server from firm^l strictly closer to i than the nearestcompetitor (within the set Ni) after the relocation. We note "lost" or "half lost" because we cannot,with simply the information that no firmv4 servers are in AT,, yet tell if the population at i is fullylost. In order to correct this uncertainfy, constraints (5) say that the population at node i is lost toa competitor (v, = 1) if there is no member of finny! either closer to / as the neaiest competitor(within the set JV,) or as close to i as the nearest competitor (within the set K,).

If there is at least one member firmyl located such that node i won't be lost to them by virtueof the relocation (set JV, empfy) qi and v, will be equal to zero, since we are minimizing. On theother hand, if there is a member firm^l within K, but not within Ni, we have that g, -1- v,- > 1 andV,- > 0 (from constraints (4) and (5)). Since the objective, relative to the loss of population, is oneof minimizing, the variable selected to be one will be qi, rather than v, since qi has the smallercoefficient. That is, only half the population in that node will be lost to a competitor.

Another possibilify which needs to be taken into account is that even if node / can be fully lostby vir1:ue of the f elocation, its population might be half lost only. This can happen when node i wascovered by both firms and after the relocation only firm C serves it. In this case, constraint (5) willforce V, to be equal to one {Ni and Ki are both empfy). In this situation v, has a coefficient of a/2 inthe objective. Note theit node / doesn't have a cohstraint in (4) since these constraints are definedonly for i in set IA (and i is doubly served prior to the relocation, hence i belongs to set IO).

Constraints (6) and (7) set the mmiber of facilities to locate and relocate. Both restrictions canbe written with inequalities, so facilities are not forced to locate and/or relocate if no improvementof the objective is achieved; j.e., if by virtue of the relocation no gain in population is obtained.

3. SOLUTION TO THE MODEL

The formulation has been solved in a 55-node connected network (Swain [9] 1974, Kroll [10] 1988)using an IBM 3090 and MPSX MIP software. Both A and C firms have three senders arbitrarilylocated on the network prior to any location/relocation. The total population covered by A is equalto 1519 (42.5% of the total population) while the competitor has a market share of 2056 people(57.5%). Suppose firm^ wants to expand its market share and decides to locate two new facilitiesand to relocate one of its existing facilities, but does not know which one. All nodes of the networkare candidates to obtain a server, including ones which have an existing server. The solution tothis problem by using the formulation above described is depicted in figure 1. By virtue of therelocation, firm^ increased its market share from 42.5% to 79.5% percent. Now its populationcovered totals 2840 while the competitor captures only 735 people. Thus, a large improvement hasbeen obtained by virtue of the relocation of the chosen facilify and the location of two new facilities.

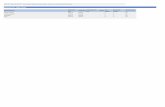
In order to test the integer properties of the model, several mns were made changing thenumbers of servers already located, new servers to locate and servers to relocate in the 5̂5 nodenetwork. More precisely, for each situation ten runs were made starting with random locations ofexisting servers. All mns were made in an IBM 3090 with a vectorized MPSX software package.Only:r; variables were declared integer. The rest were bounded by 1. Run times are not shown sincethey were negligible (less than 1 second of CPU time, including branch and bound when necessary).Table 1 presents the results.

The solutions presented in table 1 show that the model is very efficient in giving integer so-lutions, regardless of the number of servers located, to locate, and to relocate. Only in 6 out of150 mns the continuous solution gave non-integer variables. In this case the maximum number of


Firm A: ° Old

O New(Arrow indicates move)

Firm C: A

Figure 1.

Table 1.

#ofNodes

555555555555555555555555555555

#ofExistingServers

(Firm A)

111111333555555

#ofNew

Serversto locate

111555222111111

#ofServers

toRelocate

111111111111555

#ofExistingServers

(Firm C)

135135135135135

lotalit ntrF OI

Runs

101010101010101010101010101010

# of Runswith Non-

IntegerSolutions

000000031110000

non-integer variables was 7 out of 55. Branch and bound was used to find the integer solutions,finding the solution after the first branching in all cases.

A number of additional problems were solved, as reported in the next section. These problemswere focussed on the question of equilibrium in the competition between servers when multiplerelocation steps are taken.

4. EXTENSIONS TO THE MODEL: A SPATIAL DUOPOLISTIC MODEL

In all market situations there are elements of conffict and elements of parallelism or mutualify ofinterests. Firms or sellers as a group have common interests in capturing the maximum marketshare, but within the group there is a conffict of interest as to which suppliers are to obtain larger


fractions of profitable sales. Classical mieroeconomic theory identifies several market strategiesthat can be used by both firms in order to achieve their goals.

The first solution to the duopoly model was developed by a French economist from the be-ginning of the last century, Agustin Cournot [11]. His model presents two firms that produce ahomogeneous product and face the same production costs. The behavior of both firms is suchthat, within a temporal framework, eaeh duopolist decides to produce the output that maximizesits profits assuming that the quantify produced by its competitor is invariant with respect to its ownproduction level. In other words, at each time period, the firm uses the competitor's prices and pro-duction level from the last period in order to search for the output level which maximizes profits.An equilibrium is reached when both firms, at a given period, do not want to change their prices andoutput levels. Observe that the Hotelling model is similar to the Cournot model: each firm reacts(with respect to location as a decision variable) on the presumption that the other firm's decisionwill remain fixed.

A more realistic oligopoly model was presented by Heinrich Von Staekelberg [12]. The Stack-elberg solution rests on the assumption that duopolists explictly recognize the interdependence oftheir actions. It assumes that each duopolist can choose between two strategies: be a follower, thatis, choose its awn production level based on the one chosen by its competitor, or a leader.

Both Cournot and Staekelberg strategies ean be applied to the location problem describe here.Suppose there are two firms that serve an area with a homogeneous product/service. Both firmsare planning to relocate and expand their number of servers in order to capture market share. Weassume in an example that each firm knows that at eaeh period the other will relocate at most twoof its suppliers. The market share of eaeh firm depends on its ovra actions and the actions andreactions of its competitor.

Firm A: O Firm C: i\Figure 2.

The Cournot-spatial strategy (CS) is such that a firm will locate and relocate its servers bymaximizing newly captured population, regardless of the location decisions of its competitor Inour example, each firm has five servers and at each time period each one is allowed to relocate twoof them. An equilibrium would be reaehed if in the next period both firms do not whish to changelocatiori. The starting point is such that firm^ covers 1424 people, firm C has 1048, and both firmscover 1103 at the same time. So Fimi^ starts with an advantage in the location. In Figure 2 werepresent the locations in the first period. In the first step, firm^ relocated two of its five serverstaking as its competitor's locations those sites in Figure 1. Firm C also relocated itwo of its five'servers, using as its frame of reference the sites occupied by firm^ in Figure 1. That is, both firmslooked back to the previous set of positions of their competitor and relocated accordingly Fiffy


iterations were conducted to examine the convergence of the model using the Cournot Strategy. Ateaeh step both firms were allowed to relocate at most two of their servers. No equilibrium point orcycling in the locational solutions were found. That is, on eaeh iteration a different location pattemwas obtained.

The basic behavior assumption of the Cournot model is rather artificial and weak. Each firmwill find it to its own advantage to cheat and undersell the other firm: neither firm takes into ac-count any interdependence between its output decision and the other firm's output decision. Sec-ond, this reaction process is a no-learning model. In spite of repeated failures to achieve overallprofit-maximization, the firms still behave in the same fashion. The following model, based onStackelberg's leader-follower assumptions corrects some of the Cournot model weaknesses.

The Staekelberg-spatial strategy is such that each firm determines its location from both lead-ership and foUowership and desires to play the role which yields the largest maximum. As an ex-ample, Ana A will act as a follower if it locates and relocates its servers by examining the perceivedsiting strategy of its competitor C for the same period, and then site its own firms in order to capturemaximum market share, given that C has or will take known steps. Observe that firmv4 is assumingthat its competitor C is acting following a Coumot-Spatial strategy, that is, that competitor C isrelocating its servers in that period without considering that firmJl will also relocate some of itsservers during the same period.

On the other hand, a firm will act as a leader if it uses the Cournot-spatial strategy, that is, ifat each period locational decisions are made regardless of any potential relocation of a competitorin the same period. So, with these follower-leader possibilities, four sequetlces are possible: (1)firm^ decides to be a leader, and C a follower; (2) C desires to be a leader, and^ a follower; (3)both desire to be leaders; or (4) both desire to be followers. Observe that (3) is the Cournot-spatialmodel, and that (1) and (2) give consistent strategical behavior, while (4) will not give either firm'santicipated outcome.

A third solution, differing from either the Coumot or Stackelberg strategies, is collusion: thatis, both firms agree to divide the market share. In this case the solution is obvious for our problem:each firm will have fiffy percent of the market. This solution can be very inefficient in the allocationof resources since there is no locational behavior. Servers of both firms could be located as far aspossible from the population nodes and still equally divide the market share.

The Stackelberg-Spatial model was applied for 200 periods in the fiffy-five node network. Eaehfirm was allowed to relocate two of its five initial servers. The first firm (firm^!) was the leaderadopting a Cournot strategy, while firm C was the follower relocating its servers in anticipation ofA taking the Cournot strategy. Again no evidence of an equilibrium or cycling was observed inthe solutions. Cycling is defined as a repetition of a previous set of location strategies. This resultindicates that at each period eaeh firm sees an advantage in relocating some of its servers. Thereis always a position that seems to improve their market share. The same occurred when both firmsacted as a follower. No steady state was obtained.

The Staekelberg-Spatial model can be transformed into a zero-sum two person game. Againthe decision to be made by both firms is where to relocate two of its servers. The game is zero-sumbecause whatever market share is lost by one of the firms goes to the other. In this case, at eaehperiod each firm chooses its strategy (to be a follower or a leader) based on the observation of itsprofit matrix. The profit indicated in the matrix is actually the market share gained by C (and lostby A) after execution of a particular pair of strategies for A and C. Gain or loss is measured againstthe previous period's market share.

The duopolist's decision problem consists of choosing an optimal strategy at each period. Butthe final outcome depends upon the strategy of both duopolists, and neither has the power to en-force his desires. In table 2 we present the profit matrix of firm C. For example^ if Firmyl decidedto be a leader and C a follower, by virtue of the relocation firm C would gain 224.5.

In this example firm C will always gain population regardless ofthe strategy both firms choose.If firm C is a risk-averter, it will most probably choose to be a follower, since it is the strategy thatmaximizes the minimum gains (maximin strategy). Following the same argument firm A would

THE MAXIMUM CAPTURE PROBLEM

Table 2. Profit Matrix for Firm C

137

FIRMCLeaderFollower

FIRM A

Leader

168224.5

Follower

116.5120.5

choose to be a follower. In this case the duopolists are consistent, and an equiMbrium for theperiod is established. Neither duopolist can increase its market share by changing its strategy/ if hisopponent's strategy remains unchanged. At each period the duopolist would choose the maximinstrategy after observing its profit matrix. It is expected that, if at each period both duopolists areconsistent with their strategies, fewer changes in the percentage of market share vvill occur. Thiscase still remains to be tested.

5. CONCLUSIONS AND FURTHER RESEARCH

The model preseiited here efficiently locates and relocates a given number of servers which facecompetition in a duopolistic setting. Location decisions are made in an effort to maximize thenet demand captured from the competitor. The model has some limitations. The model does notallow the location of more than one server belonging to the same firm at the same node. Thiswould be necessary if one of the nodes is already occupied by one of the competitors' servers, andthe maximization solution is sueh that two (or more) servers from firm^l are needed at that node,therefore capturing two-thirds of the demand at that node. This can happen if the node has a verylarge demand with respect to the other nodes. Although the circumstance could occur in which itwould be desirable and optimal to locate two firm^ servers at a site, there is no provision in themodel to place two A servers at the same site. We hope to remedy this inconvenience in a futuremodel. A way that may avoid this problem is to subdivide the node into smaller ones with zerodistances between them in order to make a more evenly distributed population, so double capturewould not be required.

The assumptions of the model are quite restrictive, since the product/service offered is ho-mogeneous and can only be differentiated by distance. Also, there is no consideration of changesin demand due to changes in distance to the server. The objective function could be modified byusing some distance-decay function instead of average distance. Doing so, however, would cre-ate the need to solve p-median type problems because the nearest facilify to a given demand nodedetermines the extent of the demand actually exerted. Hence, variables that represent pairing ofdemand nodes wth their nearest facilify would be necessary. Finally, location and relocation costsare not considered.

The computational results presented in this paper show that the model is extremely efficientin finding integer solutions for a medium-size network. Most of the time no branch and bound hasbeen required in order to obtain integer solutions.

The application of the model has a great potential to examine duopolistic locational behavior.Here we have presented two duopolistie strategies based on the Coumot and Staekelberg mieore-conomie models which show that there is not a clear equilibrium locational point where no sender isrelocated without the loss of market capture. These strategies can be easily extended to an oligopolymarket, where several firms compete for market share.

The locational game introduces a new insight in the study of locational behavior under compe-tition since it combines aspects of game theory with strategies that are relatively easy to identify andapply to a given duopolist market. The examination of more complex strategies and competitivesituations appear to be fruitful areas of future research.

Other areas for extension include empirical investigations of location strtitegies. That is, sup-pose a new small player enters the market. Is there a stable strategy chosen by the new player —Le. locating "on top of" the existing competition or is there a better move toward new and open


ground? Suppose a larger player is expanding against (a) smaller competitor(s). Is the "locate ontop" strategy followed nearly uniformly? We did not explore these questions. All our energies weredevoted to the task of seeing first that the formulation worked. We think, nonetheless, that thesewould be fascinating questions to explore.

6. ACNOWLEDGMENTS

This research was conducted in part using the Cornell National Supercomputer Faeilify, a resourceof the Center for Theory and Simulation in Science and Engineering and Comell Universify, whichis funded in part by the National Science Foundation, New York State, the IBM Corporation andmembers of the Corporate Research Institute.

We thank the reviewers for insightful comments that helped us to explain the work and itsimpHcations more fully.

REEERENCES

[1] Hotelling, II. (1929): "Stability in Competition", Economic Joumal 39,41-57.[2] Teitz, M.B. (1968): "Locational Strategies for Competitive Systems", Joumal of Regional Science 8,135-

148[3] Eishelt H. and Laporte G. (1987): "Trading Areas of Facilities with Different Sizes". Paper G-87-12, Les

Cahiers du G E R A D , Ecole des Hautes Etudes Commercials, Universite de Montreal.[4] Eiselt, H. and Laporte, G. (1987): "Location of a new Facility on a Linear Market in the Presence of

Weights". University de Montreal: Centre de Recherche sur les Transports.[5] Dobson, G. and Karmarkar U. (1987): "Competitive location on a Network". Operations Research 35,4,

565-574.[6] Hakimi S. (1981): "On locating Hew Facilities in a Competitive Environment". International S5miposium

on location Decisions II, Copenhaguen, Denmark.[7] ReVelle, C. (1986): "The Maximum Capture or "Sphere of Influence" location Problem: Hotelling Re-

visited on a Network". Joumal of Regional Science 26,2,343-357.[8] Church, R. and ReVelle, C. (1974): "The Maximal Covering location Problem". Papers of the Regional

Science Association, 32; 101-118.[9] Swain, R. (1974): "A Parametric Decomposition Approach for the Solution of Uncapacitated location

Problems. Management Science, 21,189-198.[10] KroU, P. (1988): The Multiple-Depot, Multiple-Tow, Multiple-Stop Delivery Problem". PhD. Disserta-

tion, The Johns Hopkins University.[11] Coumot, A. (1897): Researches into the Mathematical Principals of Theory of Wealth. New York: MacMil-

lan press[12] Von Stackelberg, H. (1934): Marktform und Gleichgewicht. Vienna, Austria: Springer (English transla-

tion: The Theory of Market Economy, Oxford: Oxford University Press, 1952.)

Charles ReVelle received a B. Chem. Eng. and the Ph.D. (environmental systemsengineering) from Cornell University. On the faculty at Comell University from 1967to 1970, he joined the faculty of The Johns Hopkins University in 1971. Professor Re-Velle's research is in three main areas: (1) the siting of emergency and other publicsector facilities; (2) water quality and water resources systems; (3) arms control strategydevelopment. He has published over a hundred and twenty articles in public sectoroperations research. With his wife, Penelope, he has written The Environment: Issuesand Choices for Society, now in its 3rd Edition, 1988, Jones and Bartlett.

Daniel Serra is currently head of the Division of Product Studies, Duratex S.A., SaoPaulo, Brazil. His position includes the development of management models to deter-mine return on investment for the firm's products. Dr. Serra graduated in Economicsfrom the Autonomous University of Barcelona (Spain) and earned his M.A. (1987) andPh.D. degrees (1989) at The Johns Hopkins University. His research interests includehierarchical location analysis, competitive location and districting models. He is alsoa faculty member of the Fundacao Getulio Vargas, where he teaches Operations Re-search and Location Analysis to graduate MBA Students.

THE MAXIMUM CAPTURE PROBLEM INCLUDING RELOCATION

Documents

Transcript of THE MAXIMUM CAPTURE PROBLEM INCLUDING RELOCATION