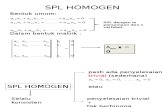
Sistem Persamaan Linear dengan N Bilangan yang Tidak Diketahui

A. Sistem persamaan Linear

Penyelesaian n persamaan linear dan n bilangan yang tidak diketahui

1. Dua persamaan liniear dengan dua bilangan yang tidak diketahui.

a) .................  a1 x + b1 y = k1 ...........(I)b)  .................  a2 x + b2 y = k2 ...........(II)

a1 dan b1 masing – masing adalah koefisien dari x dan y, k1 = konstanta

(I) ×a2≫a1a2 x+a2b2 y=a2 k1

(II)×a1 ≫a1a2 x+a1b2 y=a1k 2

(a1b2−a2b1 ) y=(a1k2−a2k1 )−¿ 

Atau

Asalkan a1 b2 – a2 b1 ≠ 0

Bila ( I ) xb

( II ) xb }    maka juga diperoleh

Asalkan a1 b2 – a2 b1 ≠ 0

Bentuk (III) dan (IV) dapat ditulis dalam bentuk determinan sebagai berikut:

Asalkan

2. Tiga persamaan linear dengan tiga bilangan yang tidak diketahui:

a) a1 x + b1y + c1z= k1 ...........(I)b) a2 x + b2 y + c2z= k2 ...........(II)c) a3 x + b3 y + c3 z = k3 ...........(III)

a1, b1, dan c1 masing masing adalah koefisien dari x, y,dan z, dan k1 = konstanta

(I)         x c2 ≫a1 c2 x+b1 c2 y+c1 c2 z=k 1c22

(II)  x c1≫a2 c1x+b2 c11 y+c1c2 z=k2c1

(a1 c2– a2 c1) x+(b1c2– b2 c1 ) y=k1 c2– k2 c1−¿

      (a1c2 – a2c1)x + (b1c2 – b2c1)y = k1c2 – k2c1 .........(IV)

(III)    x c3 ≫a2 c3 x+b2 c3 y+c2 c3 z=k2 c3

(IV)   xc2≫a3c2 x+b3c2 y+c3 c2 z=k3 c2

(a2c3– a3 c2 )x+(b2 c3– b3 c2) y=k 2c3– k3 c2−¿

          (a2c3 – a3c2)x + (b2c3 – b3c2)y = k2c3 – k3c2 .........(V)

Dari [(IV) x (b2c3 – b3c2) – (V) x (b1c2 – b2c1)] diperoleh suatu kesamaan dengan ruas kiri

[(a1c2 – a2c1)(b2c3 – b3c2) – (a2c3 – a3c2)(b1c2 – b2c1)] x dan ruas kanan yaitu:

(k1c2 – k2c1)(b2c3 – b3c2) – (k2c3 – k3c2)(b1c2 – b2c1)

Pada ruas kiri , koefisien dari x adalah

(a1b2c2c3 – a2b2c1c3 – a1b3c2 + a2b3c1c2) – (a2b1c2c3 + a3b1c2 – a2b2c1c3 + a3b2c1c2)

= a1b2c2c3 -  a1b3c2 + a2b3c1c2 – a2b1c2c3 + a3b1c2 – a3b2c1c2

=c2(a1b2c3 + a2b3c1 + a3b1c2 – a3b2c1 – a2b1c3 – a1b3c2)

Sedang ruas kanan menjadi:

(k1b2c2c3 – k2b2c1c3 – k1b3c2 + k2b3c1c2) – (k1b1c2c3 – k3b1c2 – k2b2c1c3 + k3b2c1c2)

= k1b2c2c3 – k1b3c2 + k2b3c1c2 – k2b1c2c3 + k3b1c2 – k3b2c1c2

= c2(k1b2c3 + k2b3c1 + k3b1c2 – k3b2c1 – k2b1c3 – k1b3c2)

Jadi harga x adalah

Asalkan koefisien dari x tidak sama dengan nol

Dengan cara perhitungan yang sama, juga diperoleh:

Asalkan penyebut tidak sama dengan nol.

Dengan demikian maka harga x, y, z yang ditulis dalam bentuk (IV), (VII) dan (VIII) dapat disajikan dalam bentuk determinan.

x=|k 1 b1 c1

k 2 b2 c2

k3 b3 c3|

|a1 b1 c1

a2 b2 c2

a3 b3 c3|y=

|a1 k1 c1

a2 k2 c2

a3 k3 c3|

|a1 b1 c1

a2 b2 c2

a3 b3 c3|; z=

|a1 b1 k1

a2 b2 k2

a3 b3 k3|

|a1 b1 c1

a2 b2 c2

a3 b3 c3|

asalkan|a1 b1 c1

a2 b2 c2

a3 b3 c3|≠0

Selanjutnya bila dinamakan:

D=|a1 b1 c1

a2 b2 c2

a3 b3 c3|; D x=|k1 b1 c1

k2 b2 c2

k3 b3 c3|; D y=|a1 k1 c1

a2 k2 c2

a3 k3 c3|; D z=|a1 b1 k1

a2 b2 k2

a3 b3 k3|

maka

D disebut determinan pokok yaitu determinan yang elemen elemennya terdiri dari koefisien koefisien parameter yang akan ditentukan besarannya

Dx adalah determinan yang diperoleh dari determinan D dimana kolom pertama (yaitu elemen elemen yang diambil dari koefisien kolom pertama (yaitu elemen elemen yang diambil dari koefisien koefisien x atau ai) diganti dengan suku suku yang diketahui

Dy diperoleh dari determinan D dimana kolom kedua (koefisien koefisien dari y atau bi) diganti dengan suku suku yang diketahui (yaitu ki)

Dz diperoleh dari determinan D dimana kolom ketiga (koefisien koefisien dari z atau ci) diganti dengan suku suku yang diketahui (yaitu ki). Jadi x, y dan z dapat disajikan sebagai berikut:

x=DxD, y=

D y

DdanZ=

DzDasalkanD≠0

3. Empat persamaan linier dengan empat bilangan-bilangan yang tidak diketahuiA1x + b1y + c1z + d1w = k1

A2x + b2y + c2z + d2w = k2

A3x + b3y + c3z + d3w = k3

A4x + b4y + c4z + d4w = k4

Dengan cara yang sama maka diperoleh

x=DxD, y=

D y

D,z=

D z

Ddanw=

DwD

Asalkan D ≠ 0

D=|a1 b1 c1 d1

a2 b2 c2 d2

a3 b3 c3 d3

a4 b4 c4 d4|; D x=|k1 b1 c1 d1

k2 b2 c2 d2

k3 b3 c3 d3

k 4 b4 c4 d4|

D y=|a1 k1 c1 d1

a2 k2 c2 d2

a3 k3 c3 d3

a4 k 4 c4 d4|; D z=|a1 b1 k1 d1

a2 b2 k2 d2

a3 b3 k3 d3

a4 b4 k 4 d 4|;Dw=|a1 b1 c1 k1

a2 b2 c2 k2

a3 b3 c3 k3

a4 b4 c4 k4|

Metode diatas dikenal dengan nama aturan cramer, metode tersebut juga berlaku untuk n persamaan linier atau linear dengan n bilangan yang tidak diketahuiPenjelasannya sebagai berikut:Bila determinan pokok D ≠ 0 maka bilangan yang tidak diketahui (parameter dari n persamaan linier tersebut, dapat ditentukan dengan cara mengganti element-elemen suatu kolom dari D yang merupakan koefisien-koefisien parameter (yang akan ditentukan besarannya) dengan suku-suku yang diketahui sehingga diperoleh harga parameter tersebut sama dengan harga determinan setelah suatu kolom dari D yang merupakan koefisien-koefisien parameter tersebut diganti dengan suku-suku yang diketahui dibagi dengan harga determinan pokok D.