Penggunaan Teorema Residu dalam

Menghitung Radiasi Terdifraksi

Dibuat Untuk Memenuhi Tugas Akhir Mata Kuliah

Fungsi Variabel Kompleks

Disusun Oleh:

Heru Wibowo (3125120198)

Program Studi Matematika

Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Negeri Jakarta

2015

2

Daftar Isi

Daftar Isi i

Daftar Gambar ii

1 PENDAHULUAN 1

1.1 Latar Belakang . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

1.2 Pembatasan Masalah . . . . . . . . . . . . . . . . . . . . . . . . 1

1.3 Rumusan Masalah . . . . . . . . . . . . . . . . . . . . . . . . . 2

1.4 Tujuan Penulisan . . . . . . . . . . . . . . . . . . . . . . . . . . 2

1.5 Manfaat Penulisan . . . . . . . . . . . . . . . . . . . . . . . . . 2

1.6 Sistematika Penulisan . . . . . . . . . . . . . . . . . . . . . . . . 3

2 PEMBAHASAN 4

2.1 Teori Dasar Residu . . . . . . . . . . . . . . . . . . . . . . . . . 4

2.2 Teorema Residu . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

2.3 Menghitung Residu . . . . . . . . . . . . . . . . . . . . . . . . . 5

3 KESIMPULAN 10

Bibliografi 11

i

Daftar Gambar

2.1 Tahap Perhitungan Residu . . . . . . . . . . . . . . . . . . . . . 6

2.2 Kontur Residu I . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

2.3 Kontur Residu II . . . . . . . . . . . . . . . . . . . . . . . . . . 9

ii

Bab 1

PENDAHULUAN

1.1 Latar Belakang

Fungsi Variabel Kompleks merupakan sutau penjabaran ilmu Matemati-

ka yang berkaitan dengan Analisis Real. Fungsi-fungsi yang ada di Variabel

Kompleks merupakan hasil fungsi-fungsi dan teorema turunan dari Analisis

Real, maka dari itu pembahasan dalam Fungsi Variabel Kompleks tidak luput

jauh dari Analisis Real. Makalah tugas akhir ini akan membahas mengenai

salah satu materi yang ada dalam Fungsi Variabel Kompleks yaitu Teori Resi-

du. Teori yang berdasarkan pada integrasi dan pengintegralan fungsi tertentu.

Teori Residu merupakan teori yang dibawa dan diperkenalkan olej James Wa-

rd Brown di tahun 2008. Teori ini memiliki fungsi yang sangat banyak dalam

menyelesaikan perhitungan-perhitungan tertentu dalam Fungsi Variabel Kom-

pleks. Teori Residu dikembangkan menjadi Teorema Residu, dimana teorema

inilah yang akan digunakan dalam setiap perhitungan-perhitungan fungsi ter-

sebut. Adapun pengaplikasian kasus yang akan digunakan dan dibahas secara

rinci dan jelas dalam makalah tugas akhir ini yaitu Radiasi Terdifraksi. Teori

Residu digunakan sevagar dasar pemikiran perhitungan Radiasi Terdifraksi.

Dengan mengaplikasikan Teorema Residu yang dihitung berdasarkan kontur-

kontur Residu tertentu yang akan dijelaskan lebih lanjut dalam makalah tugas

akhir ini untuk menyelesaikan permasalahan Radiasi Terdifraksi serta juga

akan dibahas pengenalan Teori Residu itu sendiri bagi para pembaca yang

masih awam atas teori tersebut. Seluruhnya akan dibahas dengan jelas dalam

makalah tugas akhir Fungsi Variabel Kompleks ini.

1

1.2 Pembatasan Masalah

Berdasarkan latar belakang di atas, maka permasalahan yang mucul ada

beberapa yang akan dibahas dalam karya tulis ini. Namun, untuk menvegah

pembahasan yang terlalu luas karena ilmu mengenai Teori Residu ini luas se-

hingga dilakukan pembatasan masalah yaitu permasalahan yang akan dibahas

adalah mengenai Teori Dasar Residu, Teorema Residu dan kemudian akan

dihitung Radiasi Terdifraksi menggunakan Teori dan Teorema Residu.

1.3 Rumusan Masalah

Berdasarkan latar belakang dan pembatasn masalah, maka dapat ditarik

beberapa rumusan masalah yaitu sebagai berikut.

1. Apa definisi dari Teori Dasar Residu?

2. Apa definisi dari Teorema Residu?

3. Bagaimana cara menghitung residu ?

1.4 Tujuan Penulisan

Tujuan penulisan dari tugas akhir ini berdasarkan rumusan masalah yaitu.

1. Mengetahui yang dimaksud dengan Teori Dasar Residu

2. Mengetahui yang dimaksud dengan Teorema Residu

3. Mengetahui Cara untuk Menghitung Residu

1.5 Manfaat Penulisan

Karya tulis ini juga memberikan beberapa manfaat antara lain yaitu.

1. Bagi Penulis :

(a) Menyelesaikan tugas akhir mata kuliah Fungsi Variabel Kompleks

(b) Mendapat Ilmu baru tentang Teori Dasar Residu dan pengaplikasi-

annya dalam menghitung radiasi terdifraksi

2

2. Bagi Pembaca :

(a) Memperkaya pengetahuan tentang Teori Dasar Residu

(b) Menjadikan sumber bacaan dan sumber informasi bagi pembaca

dan peneliti selanjutnya pada topik pembahasan yang sama

1.6 Sistematika Penulisan

Karya tulis ini secara keseluruhan terdiri dari 3 bab yaitu Pendahuluan,

Pembahasan dan Kesimpulan, dilengkapi dengan daftar pustaka yang memuat

sumber-sumber materi referensi. Sistematika pembahasan pada tugas akhir ini

adalah sebagai berikut : Bab I Pendahuluan, pada bab ini dijelaskan tentang

latar belakang masalah, perumusan masalah yang dihadapi di dalam menyusun

karya tulis, pembatasan masalah, tujuan dibuatnya karya tulis dan sistemati-

ka pembahasan laporan karya tulis yang menjelaskan sekilas dari isi tiap bab

yang terdapat pada karya tulis ini. Bab II Pembahasan, pada bab ini dibahas

mengenai Teori Dasar Residu, Teorema Residu dan Cara Menghitung Resi-

du pada Radiasi Terdifraksi. Bab III Kesimpulan, bab ini merupakan bab

akhir laporan yang memuat kesimpulan dari pembahasan masalah yang ada

dalam karya tulis ini. Selain itu juga dimuat mengenai saran-saran penulis

untuk mengembangkan sistem pendukung keputusan dalam tugas akhir ini.

Dan terakhir daftar pustaka pada bagian akhir makalah yang memuat daftar

sumber materi yang ada dalam karya tulis ini.

3

Bab 2

PEMBAHASAN

Dalam pengaplikasian untuk menghitung Residu dalam Radiasi Terdifrak-

si sebelumnya perlu diketahui terlebih dahulu dasar-dasar dari Teori Residu.

Teori Dasar Residu inilah yang akan membangun pemikiran mengenai perhi-

tungan Residu dan dalam pengaplikasiannya. Tahap selanjutnya dapat diketa-

hui pula Teorema Dasar Residu yang digunakan untuk mendasari perhitungan

Residu dalam Radiasi Terdifraksi.

2.1 Teori Dasar Residu

Berikut ini akan diuraikan Teori Dasar Residu yang nantinya akan digu-

nakan sebagai alat untuk pemodelan. Teori ini diambil dari (James Ward

Brown, 2008). Misalkan f(z) adalah fungsi kompleks yang bernilai tunggal

dan analitik di dalam dan pada suatu daerah R, kecuali di titik singularnya.

Tujuan kita adalah menghitung integral berikut .

∮C0

f(z)dz (2.1)

Dimana C0 adalah lingkaran yang pusatnya di z0, dimana f memiliki si-

ngularitas di titik pusat tersebut. Asumsikan bahwa jari-jari C0 cukup kecil

sehingga fungsi f tidak memiliki titik singular yang lain. Asumsikan pula bah-

wa arah C0 berlawanan dengan arah jarum jam.

Di sekitar titik z0, f(z) dapat dinyatakan sebagai deret Laurent yang di-

berikan oleh

4

f(z) =∞∑

k=−∞

ak(z − z0)k (2.2)

Dengan demikian, persamaan (2.2) dapat dituliskan sebagai berikut∮C0

f(z)dz =

∮C0

∞∑k=−∞

ak(z − z0)kdz =∞∑

k=−∞

ak

∮C0

(z − z0)kdz (2.3)

Ingat bahwa dengan menggunakan teorema integral Cauchy, kita dapat mem-

peroleh ∮C0

(z − z0)kdz =

{0, k 6= −1

2πi, k = −1(2.4)

Substitusikan (2.3) ke dalam (2.4) diperoleh∮C0

f(z)dz =∞∑

k=−∞

ak

∮C0

(z − z0)kdz =

{0, k 6= −1

2πi, k = −1

}= 2πia−1 (2.5)

Hal ini menunjukkan bahwa koefisien a−1 dalam deret Laurent dari fungsi

f di sekitar titik z0 menentukan nilai integral f atas lingkaran cukup kecil yang

berpusat di z0. Nilai a−1 disebut residu f di z0, dan dilambangkan dengan

Resz0(f).

2.2 Teorema Residu

Teorema 2.2.1. Misalkan f adalah fungsi bernilai tunggal di daerah R, dan

misalkan C adalah loop sederhana yang memiliki orientasi berlawanan arah

jarum jam. Asumsikan C mengelilingi himpunan titik z0, z1, z2, . dan fungsi f

mungkin tidak analitik di titik-titik tersebut. Asumsikan pula bahwa f analitik

di titik-titik lainnya pada dan di dalam C. Maka,∮C0

f(z)dz = 2πi∑k

Reszz(f) (2.6)

Teorema residu dapat dilihat sebagai perluasan dari teorema integral Cauchy.

2.3 Menghitung Residu

Untuk memperoleh residu dari suatu fungsi f(z) di z = a, pertama-tama

f(z) harus diuraikan ke dalam deret Laurent di sekitar z = a. Tetapi jika

5

z = a adalah suatu titik singular bertingkat k, maka terdapat suatu rumus

sederhana untuk a−1 yang diberikan oleh

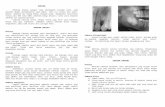
Gambar 2.1: Tahap Perhitungan Residu

a−1 = limx→a

1

(k − 1)!

dk−1

dzk−1

[(z − a)kf(z)

](2.7)

Total radiasi yang terdifrasikan dapat dihitung dengan memecahkan integral

berikut:

∞∫−∞

sin2ξ

ξ2dξ (2.8)

Dengan ξ adalah variabel posisi dan I intensitas. Melalui teknik integrasi

perbagian, yakni dengan mengambil u =sin2ξ dan dv = 1ξ2

, integral tersebut

dapat diubah menjadi :

∞∫−∞

sin2ξ

ξ2dξ = − sin2ξ

ξ+

∞∫−∞

sin 2ξ

ξdξ =

∞∫−∞

sin 2ξ

ξdξ (2.9)

Ruas kanan persamaan diatas dapat dituliskan kembali sebagai:

∞∫−∞

sin 2ξ

ξdξ =

∞∫−∞

sinx

xdx (2.10)

Dengan x = 2ξ

6

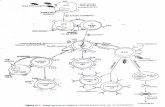
Gambar 2.2: Kontur Residu I

Untuk memecahkannya ruas kanan integral diatas, kita dapat lakukan dengan

meninjau integral kontur berikut

∮C

eiz

zdz = 0 (2.11)

Dengan kontur C yang dipilih diberikan pada Gambar 2.2, kontur terse-

but dipilih agar titik singularitas di z = z0 = 0 tidak berada dalam daerah

yang dilingkupinya, sehingga integral (2.11) berlaku. Berdasarkan pola kontur

yang dipilih tersebut, maka integral (2.11) dapat diuraikan menjadi bebera-

pa bagian, yang terkait dengan lintasan lintasan pada Gambar 2.2, sebagai

berikut:

Selanjutnya tinjauan integral yang terkait dengan lintasan II dengan mengam-

bil limit r → 0 diperoleh:

dan tinjau pula integral untuk lintasan IV dengan mengambil limit R→∞ :

7

dengan menuliskan Rexp(iϕ) = R cosϕ+ iR sinϕ diperoleh

Sehingga dengan demikian untuk kedua limit, r → 0 dan R→∞, persamaan

menjadi:

∞∫−∞

eix

xdx− iπ = 0 (2.12)

Dengan mengambil bagian imajiner persamaan (2.12) diperoleh

∞∫−∞

sinx

xdx = π (2.13)

Perlu ditekankan di sini, bahwa pengambilan kontur C yang diberikan pa-

da Gambar 2.2 bukanlah satu-satunya bentuk yang dapat diambil. Kita da-

pat pula mengambil kontur lain seperti yang diberikan dalam Gambar 2.3.

Perhatikan, dalam integral kontur terkait bentuk integral yang dicari masing

ditampung didalamnya.

Gambar 2.3: Kontur Residu II

Berbeda dengan kontur sebelumnya, dalam kontur pada Gambar 2.3 z0 ber-

ada di dalam daerah dilingkupinya, sehingga kita dapat menggunakan teorema

residu:

8

∞∮−∞

F (Z)dz = 2iπf(z0) (2.14)

Dengan F (z) = eiz

zdan f(z0) = lim

z→0zF (z) = 1 karena z = 0 adalah kutub

sederhana. Integral untuk masing masing lintasan diberikan oleh:

Perhatikan bahwa integral untuk lintasan II memiliki batas dari Φ = π sampai

2π, dan melalui cara yang sama, untuk limit r → 0 dan R→∞ diperoleh:

∞∮−∞

eix

xdx+ iπ = 2iπ (2.15)

Sehingga jelas persamaan (2.12) dan (2.13) dapat dihasilkan kembali.

9

Bab 3

KESIMPULAN

Berdasarkan pembahasan secara jelas dan rinci pada bab sebelumnya, peng-

gunaan Teorema Residu dalam Menghitung Radiasi Terdifraksi tidak luput

dari penggunaan integral dan ilmu-ilmu Analisis Real. Didasari dengan pen-

jabaran Teori Dasar Residu, penggunaan Teorema Residu yang berhubung-

an dengan Radiasi Terdifraksi dan perhitungan dengan menggunakan tahapan

perhitungan yang mengaplikasikan kontur-kontur residu di dalam perhitungan-

nya.

Berikut di bawah ini merupakan beberapa kesimpulan yang dapat ditarik

dari hasil penjabaran pada bab sebelumnya yaitu sebagai berikut:

1. Pada persamaan (2.5) diperoleh fungsi Teori Dasar Residu yaitu

∮C0

f(z)dz =∞∑

k=−∞ak

∮C0

(z − z0)kdz =

{0, k 6= −1

2πi, k = −1

}= 2πia−1

2. Nilai a−1 disebut residu f di z0, dan dilambangkan dengan Resz0(f)

3. Teorema Residu menurut Teorema 2.2.1 dihasilkan pada persamaan

(2.6) yaitu sebagai berikut

∮C0

f(z)dz = 2πi∑k

Reszz(f)

4. Hasil perhitungan Radiasi Terdifraksi dengan menggunakan Teorema Re-

sidu dihasilkan pada persamaan (2.12) dan (2.13).

10

Bibliografi

[1] Bartle. 1985. Introduction to Real Analysis. John Wiley Sons, Inc.

[2] Cgurchill, Ruel V. 1978. Complex Variables and Applications. Mc-Graw

Hill.

[3] Wade, W.R. 2000. An Introduction to Analysis. Prentice Hall.

[4] Zeidler, Eberhard. 1995. Applied Functional Analysis. Springer-Verlag New

York, Inc.

11