UKURAN GEJALA PUSAT · 2016. 9. 16. · Rumus varians populasi: ¦ 2 n Xi X 2 V Rumus varians...
Transcript of UKURAN GEJALA PUSAT · 2016. 9. 16. · Rumus varians populasi: ¦ 2 n Xi X 2 V Rumus varians...

1
PEMBELAJARAN 1
UKURAN GEJALA PUSAT
Kompetensi Dasar
Mahasiswa memahami tentang uji ukuran gejala pusat yang terdiri dari
means, modus, median, kuartil, desil, persentil, dan variabilitas, , serta mampu
menggunakannya untuk menganalisis data kuantitatif.
Indikator pencapaian
Mahasiswa dapat:
a. menjelaskan , menghitung, dan menerapkannya means untuk analisis
statistik.
b. menjelaskan , menghitung, dan menerapkannya modus untuk analisis
statistik.
c. menjelaskan , menghitung, dan menerapkannya median untuk
analisis statistik.
d. menjelaskan , menghitung, dan menerapkannya kuartil untuk analisis
statistik.
e. menjelaskan , menghitung, dan menerapkannya desil untuk analisis
statistik.
f. menjelaskan , menghitung, dan menerapkannya persentil untuk
analisis statistik.
g. menjelaskan , menghitung, dan menerapkannya variabilitas untuk
analisis statistik.

2
Uraian Materi
Setiap penelitian selalu berkenaan dengan sekelompok data. Yang
dimaksud kelompok disini adalah: Satu orang mempunyai sekelompok data,
atau sekelompok orang mempunyai satu macam data lain. Dalam
penelitian, peneliti akan memperoleh sekelompok data variabel tertentu dari
sekelompok responden, atau obyek yang diteliti. Misalnya melakukan penelitian
tentang motivasi pegawai di yayasan A, maka peneliti akan mendapatkan data
tentang motivasi pegawai di yayasan A tersebut. Prinsip dasar dari penjelasan
terhadap kelompok yang diteliti adalah bahwa penjelasan yang diberikan harus
betul-betul mewakili seluruh kelompok pegawai di yayasan A tersebut.
Beberapa teknik untuk menjelaskan kelompok yang diobservasi dengan
data kuantitatif, selain dapat dijelaskan dengan menggunakan tabel dan grafik,
dapat juga dijelaskan menggunakan teknik statistik yang disebut mean, median,
modus, kuartil, desil, maupun persentil. Teknik-teknik tersebut termasuk dalam
golongan statistik deskriptif.
A. Mean (Rata-Rata Hitung)
Merupakan teknik penjelasan kelompok yang didasarkan atas nilai
rata-rata dari kelompok tersebut. Rata-rata (mean) biasanya disimbolkan dengan
X , dan dapat diperoleh dengan cara sesuai dengan bentuk datanya, yaitu:
1. Data mentah yang belum disusun dalam bentuk distribusi frekuensi,
dalam mencari rata-ratanya sebagai berikut:
X = n
XnXXX ...........321
dimana:
X = rata-rata hitung yang dicari
X1, X2, X3, ....Xn = skor individual
n = jumlah subyek data
Contoh: Data mentah nilai matematika 45 siswa sebelum disusun dalam
tabel 4.1 sebagai berikut.

3
X = 2,645
279
45
6......109105766
2. data distribusi tunggal
X = n
fX dimana: fX = jumlah skor X frekuensi
3. data distribusi kelompok
Terdapat dua cara penghitungan:
Berdasarkan jumlah frekuensi titik tengah, caranya:
a. menentukan titik tengah (Xt) tiap kelas interval
b. memperlakukan Xt sebagaimana skor (X) pada distribusi tunggal
c. rumus: X = n
fXt , dimana fXt = jumlah dari titik tengah X
frek
d. Contoh: berdasarkan tabel 5 distribusi kelompok
Tabel 1.2: penghitungan mean dari distribusi kelompok
No Interval Frekuensi (f)
TT
(Xt) fXt
1 75-79 2 77 154
2 70-74 3 72 216
3 65-69 5 67 335
4 60-64 4 62 248
5 55-59 6 57 342
6 50-54 8 52 416
7 45-49 7 47 329
8 40-44 5 42 210
9 35-39 5 37 185

4
10 30-34 3 32 96
11 25-29 2 27 54
Jumlah 50 2585
X = 7,5150
2585
Berdasarkan rata-rata hitung duga
X = X d +i
n
fd dimana:
X d = rata-rata hitung duga
i = interval
d = deviasi
a. X d adalah titik tengah kelas yang letaknya kurang lebih ditengah
dan mempunyai frekuensi tertinggi. Dari tabel diatas, adalah 52
(pada interval 50-54 dengan frekuensi 8).
b. Menentukan besarnya deviasi (d) yang merupakan penyimpangan
dari rata-rata hitung duga. Pada tabel diatas kelas yang titik
tengahnya merupakan X d = 0, pada kelas diatasnya berturut-turut
+1, +2, +3....dst. Pada kelas bawahnya berturut-turut -1, -2, -3........dst
c. Menentukan besarnya interval, yaitu 5
Tabel 1.3: penghitungan mean dari distribusi kelompok
No Interval
Frekuensi
(f) TT d Fd fd2
1 75-79 2 77 5 10 50
2 70-74 3 72 4 12 48
3 65-69 5 67 3 15 45

5
4 60-64 4 62 2 8 16
5 55-59 6 57 1 6 6
6 50-54 8 52 0 0 0
7 45-49 7 47 -1 -7 7
8 40-44 5 42 -2 -10 20
9 35-39 5 37 -3 -15 45
10 30-34 3 32 -4 -12 48
11 25-29 2 27 -5 -10 50
Jumlah 50 0 -3 335
X = X d + i
n
fd= 52 + 5
50
3= 52 + 5 (-0,06) = 51,7
Jika penghitungan menggunakan data kasar (contoh data sebelum
dimasukkan tabel 4), maka X = 51,96
Terdapat perbedaan sebesar 51,96-51,7=0,26
51,96 merupakan X yang sesungguhnya
Adanya perbedaan tersebut disebabkan oleh grouping error /
kesalahan pengelompokan dari data kasar ke dalam distribusi
kelompok
B. Modus (Mode)
Merupakan teknik penjelasan kelompok yang didasarkan atas nilai yang
paling sering muncul dalam kelompok tersebut. Apabila dalam kelompok
data tersebut skornya mempunyai frekuensi yang sama, maka data tersebut
tidak memiliki modus. Sedangkan jika terdapat dua skor yang frekuensinya
sama, maka kedua skor dijumlah kemudian dibagi 2.

6
Pada data distribusi tunggal (contohnya tabel 4), modusnya adalah 6
karena mempunyai frekuensi tertinggi yaitu 14.Sedangkan pada distribusi
kelompok, maka
Mo = B +
1_1
1
ffoffo
ffoX i dimana:
Mo = modus yang dicari
B = Batas bawah dari kelas modus
fo = frekuensi kelas modus
f1 = frekuensi diatas kelas modus
f-1= frekuensi dibawah kelas modus
i = interval
dari tabel 5, maka modusnya adalah
Mo = 49,5 +
7868
68X 5 = 49,5 + (0,667X5) = 52,83
C. Median (Md)
Merupakan salah satu teknik penjelasan kelompok yang didasarkan atas nilai
tengah dari kelompok data yang telah disusun urutannya dari yang terkecil
sampai yang terbesar, atau sebaliknya dari yang terbesar sampai yang
terkecil
Jika n ganjil, maka Md = (n + 1) : 2
Contoh: data 21, 22, 23, 24, 25, 25, 26
Maka Md = (7 + 1) : 2 = 8 : 2 = 4
Jadi mediannya adalah bilangan ke-4 yaitu 24
Jika n genap, maka Md = n : 2
Contoh: data 21, 22, 23, 24, 25, 25, 26, 27

7
Maka Md = 8 : 2 = 4
Yang dimaksud adalah bilangan ke-4 dan ke-5 dijumlah dan dibagi 2
Md = (24 + 25) : 2 = 24,5
Jika data berdistribusi kelompok, maka Md = B + fmd
fkbn 2/ X i
Md = nilai median yang dicari
B = batas bawah kelas tempat median berada
fkb = jumlah frekuensi di kelas yang terletah di bawahnya.
fmd = jumlah frekuensi kelas tempat median berada
i = interval
Contoh dari tabel 7, maka mediannya adalah:
Md = 49,5 + 58
222/50x
= 49,5 + 1,875 = 51,375
D. Kuartil (K)
Merupakan bilangan yang membagi data menjadi empat sub kelompok data.
Kuartil 1, kuartil 2, kuartil 3
Untuk data distribusi tunggal, Ki = skor ke i x 4
1n
Ki = kuartil ke i
N = jumlah data
Contoh: data 3, 3, 5, 5, 6, 7, 7, 7, 8, 9, 10, 10, 10, 11, 12, 12
Maka K3 = skor ke 3 x 4
116 = skor ke 12 ¾
= skor ke 12 + ¾ (skor ke-13 – skor ke-12)
= 10 + ¾ ( 10 - 10 )
= 10 + 0

8
= 10
Untuk data distribusi kelompok
Ki = B + fd
fkbni 4/ x i
Ki = kuartil ke i
n = jumlah data
B = batas bawah pada interval yang mengandung kuartil
fkb = frekuensi kumulatif di bawah kelas yang mengandung kuartil
fd = frekuensi kelas yang mengandung kuartil
i = interval
contoh : untuk menghitung K1
Tabel 1.4: distribusi frekuensi kelompok
No Interval Frekuensi TT FK
1 75-79 2 77 50
2 70-74 3 72 48
3 65-69 5 67 45
4 60-64 4 62 40
5 55-59 6 57 36
6 50-54 8 52 30
7 45-49 7 47 22
8 40-44 5 42 15
9 35-39 5 37 10
10 30-34 3 32 5

9
11 25-29 2 27 2
Jumlah 50
Dari tabel di atas diketahui:
¼ n = ¼ x 50 = 12,5 (terletak pada FK 15, interval 40-44)
fd = 5
fkb = 10
B = 39,5
i = 5
Maka harga K1 = 39,5 + 5
105,12 x 5 = 42
Dengan perhitungan yang sama, maka K2 = 51,375, K3 = 61. Sehingga
apabila dibuat norma pengukuran berdasarkan nilai kuartil adalah
sebagai berikut:
Jenis kuartil Nilai Kategori
Baik
Sekali
K3 61
Baik
K2 51,375
Sedang
K3 42

10
Tidak
Baik
E. Desil
Merupakan bilangan yang membagi data menjadi sepuluh sub kelompok
data.
Sehingga terdapat D1 sampai D9
Untuk data distribusi tunggal, Di = skor ke i x 10
1n
Di = desil ke i
n = jumlah data
Contoh: data 3, 3, 5, 5, 6, 7, 7, 7, 8, 9, 10, 10, 10, 11, 12, 12
Maka D4 = skor ke 4 x 10
116 = skor ke 6,8
= skor ke 6 + 0,8 (skor ke-7 – skor ke-6)
= 7 + 0,8 ( 7 - 7 )
= 7 + 0
= 7
Untuk data distribusi kelompok
Di = B + fd
fkbni 10/ x i
Di = desil ke i
n = jumlah data
B = batas bawah pada interval yang mengandung kuartil
fkb = frekuensi kumulatif di bawah kelas yang mengandung kuartil

11
fd = frekuensi kelas yang mengandung kuartil
i = interval
Berdasarkan tabel 11, untuk mencari D6, diketahui:
6/10 n = 6/10 x 50 = 30 (terletak pada FK 30, interval 50-54)
fd = 8
fkb = 22
B = 49,5
i = 5
Maka harga D6 = 49,5 + 8
2230 x 5 = 54,5
F. Persentil
Merupakan bilangan yang membagi data menjadi seratus sub kelompok
data.
Sehingga terdapat P1 sampai P99
Untuk data distribusi tunggal, Pi = skor ke i x 100
1n
Pi = desil ke i
n = jumlah data
Contoh: data 3, 3, 5, 5, 6, 7, 7, 7, 8, 9, 10, 10, 10, 11, 12, 12
Maka P60 = skor ke 60 x 100
116 = skor ke 10,2
= skor ke 10 + 0,2 (skor ke-11 – skor ke-10)
= 9 + 0,2 ( 10 - 9 )
= 9 + 0,2
= 9,2

12
Untuk data distribusi kelompok
Pi = B + fd
fkbni 100/ x i
Pi = persentil ke i
n = jumlah data
B = batas bawah pada interval yang mengandung kuartil
fkb = frekuensi kumulatif di bawah kelas yang mengandung kuartil
fd = frekuensi kelas yang mengandung kuartil
i = interval
Berdasarkan tabel 11, untuk mencari P75, diketahui:
75/100 n = 75/100 x 50 = 37,5 (terletak pada FK 40, interval 60-64)
fd = 4
fkb = 36
B = 59,5
i = 5
Maka harga P75 = 59,5 + 4
365,37 x 5 = 61,375
G. Variabilitas
Variabilitas adalah ukuran tentang derajat penyebaran nilai-nilai variabel
(variasi) dari suatu tendensi sentral dalam sebuah distribusi. Untuk mengetahui
tingkat variasi kelompok data dapat dilakukan dengan melihat rentang data
(range), varians, standar deviasi atau simpangan baku dari kelompok data yang
telah diketahui tersebut.
1. Rentang data (Range)
Digunakan untuk mengetahui tingkat homogenitas suatu data
Range = (Nilai tertinggi – Nilai terendah) +1

13
Contoh:
Tabel 1.5: homogenitas data
Data A Data B
24, 24, 25, 25, 25, 26, 26 16, 19, 22, 25, 28, 30, 35
X = n
X= 25
7
175 X =
n
X= 25
7
175
Range = (26-24)+1 = 3 Range = (35-16)+1 = 20
Distribusi lebih homogen Distribusi lebih heterogen
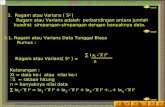
2. Varians
Varians merupakan jumlah kuadrat semua deviasi nilai-nilai individual
terhadap rata-rata kelompok. Contoh menghitung dan tabel penolong untuk
varians pada data kelompok diberikan pada tabel 14.
Rumus varians populasi:
n
XXi2
2
Rumus varians sampel:
2
2
1
n
XXis
3. Standar Deviasi / Simpangan Baku
Merupakan suatu ukuran untuk mengetahui seberapa besar penyimpangan
dalam sebuah distribusi atau disebut juga sebagai akar varians. Contoh
menghitung dan tabel penolong untuk standar deviasi data kelompok
diberikan pada tabel 14.
Rumus simpangan baku populasi:
n
XXi2
Rumus simpangan baku sampel:
1
2
n
XXis
a Penghitungan standar deviasi dari penyimpangan skor individual

14
Dari tabel 5.5, dapat disusun tabel kerja sebagai berikut:
Tabel 1.6: simpangan baku skor individual
X x = X - X x2 X x = X - X x2
24 -1 1 16 -9 81
24 -1 1 19 -6 36
25 0 0 22 -3 9
25 0 0 25 0 0
25 0 0 28 3 9
26 1 1 30 5 25
26 1 1 35 10 100
jumlah 0 4 jumlah 0 260
s = n
x 2
s = n
x 2
s = 7
4 s =
7
260
s = 0,75 s = 6,09
b Penghitungan standar deviasi untuk data distribusi tunggal
Tabel 5.7: simpangan baku skor individual
No Nilai (X)
Frekuensi
(f) fX fX2
1 4 7 28 112
2 5 9 45 225

15
3 6 14 84 504
4 7 6 42 294
5 8 3 24 192
6 9 4 36 324
7 10 2 20 200
Jumlah 45 279 1851
s =
n
n
fXfX
2
2
= 45
45
2791851
2
= 45
2,121= 1,64
c Penghitungan standar deviasi untuk data distribusi kelompok
dengan cara frekuensi titik tengah
s =
1
2
n
XXtf dimana:
f = frekuensi
Xt = titik tengah
X = rata-rata hitung
Berdasarkan tabel 10 diketahui bahwa X = 51,7, maka untuk
menghitung simpangan baku disusun tabel kerja sebagai berikut:
Tabel 1.8: menghitung simpangan baku
No Interval
Frekuensi
(f)
TT
(Xt) (Xi- X )
(Xi- X
)2 f (Xi- X )2
1 75-79 2 77 25.3 640.09 1280.18
2 70-74 3 72 20.3 412.09 1236.27

16
3 65-69 5 67 15.3 234.09 1170.45
4 60-64 4 62 10.3 106.09 424.36
5 55-59 6 57 5.3 28.09 168.54
6 50-54 8 52 0.3 0.09 0.72
7 45-49 7 47 -4.7 22.09 154.63
8 40-44 5 42 -9.7 94.09 470.45
9 35-39 5 37 -14.7 216.09 1080.45
10 30-34 3 32 -19.7 388.09 1164.27
11 25-29 2 27 -24.7 610.09 1220.18
Jumlah 50 8370.5
s = 150
5,8370
= 13,07
dengan cara rata-rata hitung duga
Tabel 1.9: menghitung rata-rata duga
No Interval
Frekuensi
(f) TT d fd fd2
1 75-79 2 77 5 10 50
2 70-74 3 72 4 12 48
3 65-69 5 67 3 15 45
4 60-64 4 62 2 8 16

17
5 55-59 6 57 1 6 6
6 50-54 8 52 0 0 0
7 45-49 7 47 -1 -7 7
8 40-44 5 42 -2 -10 20
9 35-39 5 37 -3 -15 45
10 30-34 3 32 -4 -12 48
11 25-29 2 27 -5 -10 50
Jumlah 50 0 -3 335
s = i
n
n
fdfd
2
2
s = 5
50
50
3335
2
= 12,939
RANGKUMAN
1. Means data mentah yang belum disusun dalam bentuk distribusi frekuensi,
dalam mencari rata-ratanya sebagai berikut:
X = n
XnXXX ...........321
2. Means untuk data distribusi tunggal
X = n
fX dimana: fX = jumlah skor X frekuensi
3. Means untuk data distribusi kelompok

18
X = n
fXt , dimana fXt = jumlah dari titik tengah X frek
4. Modus untuk distribusi kelompok
Mo = B +
1_1
1
ffoffo
ffoX i dimana:
5. Median pada data berdistribusi kelompok, maka
Md = B + fmd
fkbn 2/ X i
6. Kuartil untuk data distribusi tunggal, Ki = skor ke i x 4
1n
7. Kuartil untuk data distribusi kelompok
Ki = B + fd
fkbni 4/ x i
8. Desil untuk data distribusi kelompok
Di = B + fd
fkbni 10/ x i
9. Persentil untuk data distribusi tunggal, Pi = skor ke i x 100
1n
10. Persentil untuk data distribusi kelompok
Pi = B + fd
fkbni 100/ x i
LATIHAN
1. Perhatikan tabel berikut ini, kemudian hitunglah mean, median dan modus
pada distribusi tunggal tersebut!
No Nilai (X)
Frekuensi
(f) fX
1 4 7 28
2 5 9 45

19
3 6 14 84
4 7 6 42
5 8 3 24
6 9 4 36
7 10 2 20
Jumlah 45 279
2. Berikut ini adalah mid point dari nila 60 orang mahasiswa beserta
frekuensinya.
Mid Point Frekuensi A Frekuensi B
55 3 15
59 15 4
63 4 3
67 19 14
71 13 19
75 6 5
Total 60 60
Buatlah distribusi Frekuensi Relatif Perbandingan, Desimal, dan Persen!
3. Dari tabel soal no.2 tentukan
Modus
Kuartil bawah
Kuartil Atas