GetaranModul Fisika

By Defrianto Pratama

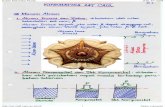
GETARAN (Gerak Harmonik) A. KINEMATIKA GETARAN 1. Gejala Getaran Gejala getaran banyak dijumpai dalam kehidupan kita sehari-hari. Senar gitar, beduk, pita suara, bandul jam dinding, dan mistar merupakan benda-benda yang dapat memperlihatkan gejala getaran. Perhatikan senar yang sedang dipetik dan beduk yang dipukul. Senar itu tampak bergerak ke atas dan kebawah secara berulang-ulang, kulit beduk juga bergerak naik turun secara berulang-ulang bila dipukul. Jika diperhatikan dengan cermat, ternyata senar dan kulit beduk bergerak naik turun secara teratur (secara periodik) dengan menempuh lintasan yang sama. Gerak periodik dengan menempuh lintasan yang sama disebut getaran. Pengertian gerak periodik itu sendiri adalah gerak benda secara berulang-ulang dalam selang waktu yang sama. Untuk lebih memahami gejala getaran, mari kita perhatikan gambar (1.1). Sebuah mistar plastik yang salahsatu ujungnya dijepit sehingga tidak dapat bergerak. Posisi benda ketika sedang tidak bergerak atau diam disebut kedudukan setimbang (b). Jika ujung mistar yang tidak dijepit ditarik kemudian dilepaskan, ujung atas mistar akan bergerak bolak-balik antara a dan c. Gerak dari a ke c kemudian kembali lagi ke a disebut satu getaran. Simpangan terjauh dariGambar 1.1 Sebuah mistar digetarkan

kedudukan seimbang (jarak dari a ke b atau b ke c) disebut amplitudo.

Perhatikan pula gambar (1.2) Sebuah beban yang terikat pada pegas dalam keadaan diam. Mula-mula beban berada pada kedudukan seimbang di b. Bila

pegas ditarik sedikit ke bawah kemudian dilepaskan, maka beban akan bergerak berulang-ulang antara c danGambar 1.2 Sebuah Pegas digetarkan

a. Beban dikatakan bergetar satu kali bila bergerak dari c ke a, lalu kembali ke c. Jarak dari a ke b atau b ke c

menyatakan amplitudo getaran.

2. Amplitudo, Periode dan Frekuensi Getaran Setiap getaran pasti memiliki amplitudo dan frekuensi. Amplitudo merupakan simpangan maksimum. Frekuensi adalah banyaknya getaran tiap sekon. Kedua besaran ini menyatakan ciri-ciri suatu getaran. Waktu yang diperlukan benda untuk melakukan satu kali getaran disebut periode. antara frekuensi dengan periode terdapat hubungan, yaitu

Dengan f = frekuensi dan T = periode. Satuan frekuensi disebut getaran/sekon atau hertz (Hz). 3. Persamaan simpangan pada Getaran Kita semua pasti pernah melihat seseorang mengendarai sepeda. Apabila kita mengamati orang yang mengendarai sepeda dari arah samping, maka kita melihat kaki pengendara bergerak melingkar untuk mengayuh pedal sepeda. Namun apabila kita melihat orang yang mengendarai sepeda tersebut dari arah depan atau belakang, maka kaki pengendara hanya terlihat bergerak naik turun melalui lintasan yang lurus.

Gambar 1.3 (a) Partikel yang bergerak melingkar (b) Proyeksi terhadap salahsatu diameternya menununjukan gerak bolak-balik

Dari persitiwa tersebut kita dapat menarik kesimpulan bahwa apabila suatu benda yang bergerak melingkar diproyeksikan ke salah satu diameternya, maka benda tersebut seolah melakukan getaran. Simpangan maksimum dari getaran itu tidak lain adalah jarijari lingkarannya. Dengan menyatakan getaran sebagai proyeksi gerak melingkar pada salah satu diameternya, maka kita dapat menentukan persamaan simpangan, persamaan kecepatan dan persamaan percepatan getaran dengan bantuan proyeksi tersebut.

a. Persamaan Gerak Harmonik Gambar (1.4) menunjukan sebuah partikel yang bergerak sepanjang lintasan lingkaran yang berjari-jari A dengan kecepatan sudut . Misalkan, mula-mula partikel berada di P1. Setelah beberapa saat (t), partikel tersebut berada di P2. Apabila titik P adalah proyeksi dari titik P2 dan OP=y maka jarak simpangan

Gambar 1.4

partikel tersebut sejak bergerak dari titik P1 ke P2 dan paertikel maka persamaan ini dapat dituliskan menjadi Persamaan simpangan gerak harmonik( )

Persamaan kecepatan gerak harmonik( )

Persamaan percepatan gerak harmonik( )

Karena

(

)

, maka

Dengan: y A t = simpangan gerak harmonik sederhana (meter) = amplitudo (meter) = kecepatan Sudut (rad/sekon) = waktu (sekon)

B. DINAMIKA GETARAN 1. Gerak Harmonik Pada bagian ini kita akan menelaah suatu jenis getaran, yaitu gerak harmonik (gerak selaras). Gerak harmonik merupakan gerak sebuah benda atau partikel dimana besarnya frekuensi tidak berubah terhadap waktu. Grafik posisi gerak harmonik, berupa fungsi waktu yang dinyatakan dalam bentuk sinusoidal (bentuk sinus atau kosinus). Dalam fisika terdapat beberapa macam gerak harmonik dan dalam pembahasan ini, kita hanya akan membahas gerak harmonik sederhana, yaitu gerak harmonik yang dipengaruhi oleh gaya yang arahnya selalu menuju titik seimbang dan besarnya sebanding dengan simpangannya.

2. Analisis Gaya Pada Gerak Harmonik Sederhana Kita telah tahu bahwa suatu benda akan bergerak jika ada suatu gaya yang bekerja padanya. Gaya yang konstan akan menghasilkan gerakan dengan percepatan konstan sehingga kita dapat menentukan posisi dengan mudah. Namun, pada gerak harmonik, resultan gaya yang bekerja padanya tidak konstan, tetapi berubah-ubah selama gerakannya berlangsung. Oleh karena itu, dengan mempelajari dan menganalisis gaya yang bekerja pada gerak harmonik, kita akan lebih mengenal dan mengetahui sifat gerak harmonik.

a. Analisis Gaya pada Getaran pegas Marilah kita amati gerak suatu benda yang terletak diatas lantai dan terikat pada sebuah pegas dengan konstanta gaya k seperti tampak pada gambar (1.6). Anggap mula-mula benda berada pada posisi sedemikian rupa sehingga pegas tidak tertekan atau teregang (gambar b) ketika kita memberikan simpangan sejauh x pada pegas, kita akan merasakan gaya yang menarik pegas untuk Gambar 1.6 adax x

kembali pada keadaan awalnya, karena

sifatnya yang selalu mengembalikan pada keadaan awal maka gaya ini dinamakan gaya pemulih. Gaya pemulih ini besarnya sama dengan gaya luar yang diberikan namun berlawanan arah.

Semakin jauh simpangan yang kita berikan maka gaya pemulih semakin besar kita rasakan, jika kita dapat mengukur besar gaya yang diberikan dan mengukur besar simpangan yang terjadi akibat gaya luar tersebut maka kita akan menemukan kesebandingan antara Fpemulih dan x sehingga dapat kita tuliskan Agar kesebandingan tersebut menjadi sebuah persamaan maka diperlukan sebuah konstanta.

Dimana k=konstanta gaya pegas. Tanda minus menunjukan bahwa gaya pemulih selalu berlawanan dengan arah simpangan.

b. Analisis Gaya pada bandul sederhana Tinjau sebuah benda bermassa m yang tergantung pada seutas tali sepanjang l dan menjalani gerak harmonik sederhana seperti tampak pada gambar (1.7).

Gambar 1.7 Terdapat dua buah gaya yang bekerja pada benda, yaitu gaya berat w = mg dan tegangan tali T. Tegangan tali T disebabkan oleh komponen berat mg cos , sedangkan komponen berat mg sin bekerja untuk melawan simpangan. Oleh karena itu, gaya pemulih pada bandul sederhana adalah( )

3. Perioda dan Frekuensi Getaran Harmonik Pada bagian sebelumnya, kita sudah sedikit membahas tentang perioda dan frekuensi secara umum. Namun secara spesifik kita juga dapat menentukan besarnya perioda dan frekunsi pada getaran Harmonik dengan meninjau gaya yang menyebabkannya.

a. Perioda dan Frekuensi pada pegas Kita dapat menghitung perioda dan frekuensi dengan menggunakan gaya pemulih dan gaya sentripetal. Gaya pemulih dinyatakan sebagai. F = -kx (1.18)

Gaya F pemulih dapat juga kita hitung dari percepatan benda dengan menggunakan hukum II newton, yaitu Fy = m ay Karena ay = - 2y maka Fy = - m dapat memperoleh rumus untuk frekuensi sudut, -m = -ky . (1.19) Dengan menyamakan ruas kanan persamaan (1-18) dan persamaan (119) kita

(1.20)

Periode T, dapat ditentukan sebagai berikut

Periode pegas

Dengan

frekuensi sudut (rad/s); T= periode (s); m = massa beban pada

ujung pegas (kg) dan k = tetapan pegas (N/m). Frekuensi pegas , f , adalah kebalikan dari periode, T , yaitu :

Frekuansi pegas

b. Perioda dan Frekuensi pada bandul sederhana Seperti halnya pada pegas, perioda dan frekuensi pada bandul sederhana dapat dihitung dengan gaya pemulih dan gaya sentripetal. Perlu ditekankan bahwa gerak

harmonik pada sederhana hanya terjadi jika sudut simpangannya cukup kecil, yaitu sin = ( dalam satuan radian), perhatikan gambar (1.8)

Gambar 1.8

Untuk yang kecil sin = sehingga berdasarkan hubungan besaran translasi dan rotasi diperoleh y = l atau =y/l sehingga

(

)

Karena f = 1/T, maka diperoleh

4. Energi Gerak Harmonik Energi potensial benda yang melakukan gerak harmonik sederhana misalnya pegas, adalah

Mengingat k = m2 dan y = A sin t, maka diperoleh

Energi kinetik benda bermassa m dan meiliki kecepatan v adalah

Pada gerak harmonik

atau

(

maka diperoleh)

Oleh karena itu, energi mekanik gerak harmonik adalah( Energi gerak harmonik )

Persamaan di atas menyatakan bahwa energi mekanik gerak harmonik adalah konstan (berlaku hukum kekekalan energimekanik). Berdasarkan persamaan energi gerak harmonik sederhana, yaitu ,( ) dan

tampak jelas bahwa setiap perubahan energi potensial selalu diikuti dengan perubahan energi kinetik.

Kerjakan Soal di Bawah Ini ! 1. Jelaskan apa yang dimaksud dengan getaran dan berikan contohnya! 2. Sebuah benda bergetar harmonik dengan simpangan sebesar 6 cm dan frekuensi 0,25 Hz. Tentukanlah besar simpangan (y), kecepatan (v) dan percepatan (a) pada saat t = 1/3 sekon adalah.. (gunakan persamaan simpangan, kecepatan dan percepatan pada gerak harmonik sederhana) 3. Sebuah bandul dengan panjang tali 0,4 m. disimpangkan sejauh 1 cm (A= 1 cm), jika percepatan gravitasi g = 10 m/s2 maka tentukan : a. Besar frekuensi dan periode bandul b. Simpangan bandul pada saat t = 1 sekon 4. Sebuah pegas dengan konstanta pegas k = 10 N/m disimpangkan sejauh 1 cm (A = 1 cm). jika massa beban m = 40 kg, tentukan : a. Besar frekuensi dan periode pegas b. Simpangan, kecepatan dan percepatan pegas pada saat t= s c. Besar energi mekanik gerak harmonik pegas 5. Sebuah pegas bergerak dengan persamaan sekon). Jika massa beban 10 kg tentukanlah : a. Konstanta pegas k b. Besar energi kinetik ketika pegas menyimpang sejauh 3 cm (y dalam cm dan t dalam

Lembar Jawaban