PerTran 6 - 1

BAB VI

TRIP ASSIGNMENT

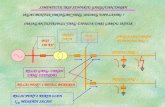
6.1. PENGANTAR

Tahap Distribusi

Tahap Distribusi

Pergerakan Antar Zona

Jar Jalan 1 Jar Jalan 2 Jar Jalan 3

Assignment

i j

PerTran 6 - 2

Tujuan Trip Assignment :

Untuk menentukan jumlah Arus di tiap ruas jalan dan total

perjalanan pada jaringan yang ditinjau

PROSES PEMBEBANAN

6.2. KRITERIA PEMILIHAN RUTE

1. Waktu tempuh

2. Jarak

3. Biaya

4. Kemacetan/Antrian Yang umum digunakan dalam

5. Jenis JR (Arteri,Tol) pertimbangan pemilihan rute :

6. Pemandangan - Jarak

7. Kelengkapan Jalan - Waktu tempuh

8. Jumlah Simpang

9. DLL

MAT

(DEMAND)

JARINGAN

(SUPPLY)

TRIP ASSIGNMENT

(PEMILIHAN RUTE)

ARUS DAN TOTAL

BIAYA PERJALANAN

KRITERIA

MEMUTUSKAN

PerTran 6 - 3

6.3. PENGGOLONGAN PEMBEBANAN

KONSEP BIAYA- ARUS

Hubungan kecepatan-arus sangat sering digunakan dalam rekayasa

lalu lintas. Konsep ini pada awalnya dikembangkan untuk ruas jalan

yang panjang pada jalan bebas hambatan.

Kecepatan (km/jam) Waktu (menit) Arus max

Arus (kend/jam) Arus (kend/jam)

GAMBAR KONSEP BIAYA ARUS

Jika arus lalu lintas meningkat kecepatan cenderung menurun

secara perlahan, dan jika arus mendekati kapasitas maka

penurunan kecepatan semakin besar, dan semakin lama semakin

tidak stabil dan mengalami jam (macet)

Model pembebanan rute yang mempertimbangkan kemacetan

memerlukan beberapa persamaan (fungsi) yang cocok untuk

menghubungkan atribut suatu ruas jalan (seperti kapasitas,

PerTran 6 - 4

kecepatan arus bebas, dan arus lalu lintas) dengan kecepatan dan

biaya yang dihasilkan. Hal dinyatakan dalam rumus berikut:

C1 = C1 ({V}) (1)

Biaya pada suatu ruas jalan l merupakan fungsi dari semua

pergerakan V pada jaringan jalan tersebut. Rumus ini cocok untuk

daerah perkotaan yang memiliki interaksi yang erat antara arus di

ruas jalan dengan tundaan di ruas jalan yang lain.

Namun bila kita mempertimbangkan ruas jalan yang panjang, rumus

tersebut dapat disederhanakan menjadi:

C1 = C1 (V) (2)

Biaya pada suatu ruas jalan hanya tergantung dari arus dan ciri

ruas itu saja. Rumus ini tidak cocok untuk daerah perkotaan yang

macet.

Kita menganggap bahwa dalam hubungan biaya-arus, biaya akan

meningkat sesuai dengan arus lalu lintasnya, kecuali pada tingkat

arus yang sangat rendah yang biayanya dainggap konstan.

Total biaya operasi pada suatu ruas jalan dapat dinyatakan dengan

C1 = C1 (V). Dalam hal ini perlu dipertimbangkan konsep biaya

PerTran 6 - 5

marginal;, yaitu kontribusi pada total biaya yang disebabkan oleh

penambahan marginal satu kendaraan pada arus lalu lintas, sbb.:

1

11

111

1

111 )()()].(.[

V

VCVVC

V

VCVCml

(3)

Pada sisi kanan persamaan ada dua komponen :

1. )( 11 VC , yang merupakan biaya rata-rata pada ruas jalan

2. 1

111

)(

V

VCV

, yang merupakan kontribusi tundaan pada arus

lalu lintas yang lain yang disebabkan oleh

kendaraan marginal (hal ini merupakan dampak

eksternal yang terkait dengan biaya tambahan

yang dirasakan oleh pengguna lainnya pada ruas

jalan tersebut yang disebabkan oleh tambahan

satu kendaraan baru)

METODE PEMILIHAN RUTE

Faktor yang dipertimbangkan dalam pemilihan rute adalah:

o Waktu tempuh faktor utama

o Jarak

o Jumlah persimpangan yang dilalui

o Kemacetan

o Rambu lalu lintas

PerTran 6 - 6

o Kondisi permukaan jalan

o Keselamatan

o Dll.

Model pemilihan rute dapat diklasifikasikan berdasarkan beberapa

faktor:

o Perbedaan persepsi pribadi tentang apa yang diartikan dengan

biaya perjalanan karena adanya perbedaan kepentingan atau

informasi yang tidak jelas dan tidak tepat mengenai kondisi

lalu lintas.

o Apakah pengaruh kemacetan di ruas jalan diperhitungkan

dalam pemodelan.

Apakah Efek Kesalahpahaman

Disertakan

Tidak Ya

Apakah Efek

Kemacetan

Disertakan?

Tidak All Or Nothing Stochastic Murni

Ya

Wardrop

Equilibrium

Deterministic User

Equilibrium (DUE)

Stochastic User

Equilibrium (SUE)

A-O-N (All Or Nothing):

Pada teknik pembebanan ini diasumsikan bahwa seseorang akan

memilih rute berdasarkan pada rute terpendek (short path)

tanpa memperhitungkan efek kemacetan sehingga berapapun

jumlah arus diruas tersebut tidak berpengaruh pada pemilihan

rute.

PerTran 6 - 7

Cara A-O-N ini lebih tepat digunakan pada ruas jalan antar

kota yang tidak mengalami kemacetan

PEMBEBANAN EQUILIBRIUM

o Asumsi dasar dari pemodelan equilibrium adalah masing-

masing pengemudi mencoba untuk meminimumkan ongkos

perjalanannya.

o Bagi pengemudi, ongkos dari semua pilihan yang ada

diasumsikan diketahui secara implisit dalam pemodelan.

o Ongkos disini menunjukkan ongkos untuk penggunaan

perjalanan, terkadang ongkos ini untuk menunjukkan

generalised cost, yakni kombinasi dari waktu tempuh, jarak

dan ongkos perjalanan lainnya seperti ongkos parkir, terminal,

transit, ongkos operasi, kenyamanan, kemudahan dan lain-lain.

Dalam konteks dengan pemilihan rute, pernyataan yang sama

dengan asumsi dasar di atas secara singkat telah dibahas oleh

Wardrop (1952). Pada tulisan tersebut diuraikan bahwa terdapat

dua perilaku intuitif yang menjelaskan bagaimana lalu lintas dapat

didistribusikan kedalam rute yang dikenal dengan Prinsip Wardrop

Equilibrium. Dua prinsip tersebut dinyatakan sebagai berikut:

(1) Under equilibrium condition traffic arranges itself in

congested networks in such a way that no individual trip

maker can reduce his path cost by switching routes.

PerTran 6 - 8

(2) Under social equlibrium condition traffic should be arranged

in congested networks in such a way that average (or total)

travel is minimised

Dari prinsip Wardrop tersebut, yang pertama dapat disimpulkan

bahwa dalam kondisi equilibrium tidak ada pengguna jalan yang

dapat mengubah rutenya untuk mendapatkan biaya perjalanan yang

lebih murah, karena semua rute yang tidak digunakan mempunyai

biaya perjalanan yang sama atau lebih besar dari pada rute yang

dilaluinya sekarang. Sehingga dapat dikatakan sistem tersebut

mencapai kondisi seimbang menurut pandangan pengguna. Oleh

karena itu prinsip ini disebut users equilibrium.

Sedangkan pada prinsip Wardrop yang kedua menyatakan bahwa

dalam kondisi optimum, total biaya sistem yang terjadi adalah

minimum. Prinsip ini kemudian dikenal dengan system optimal.

Keduanya saat ini telah menjadi standar praktis dalam setiap

evaluasi perencanaan transportasi yang didasarkan pada metode

equilibrium.

Pada umumnya arus yang dihasilkan dari dua prinsip tersebut tidak

sama, tetapi dalam prakteknya, lalu lintas mengatur dirinya sendiri

mengikuti pendekatan prinsip wardrop yang pertama (users

equilibrium).

PerTran 6 - 9

FORMULASI PEMBEBANAN EQUILIBRIUM

Pembebanan dikatakan memenuhi prinsip Wardrop pertama jika

semua rute yang digunakan (untuk setiap pasang OD) harus

mempunyai biaya perjalanan yang lebih kecil (minimum) atau sama

dibandingkan dengan rute yang tidak digunakan. Secara matematis

prinsip tersebut dapat dinyatakan sebagai :

= *

ijC untuk seluruh 0* ijT

Cpij =

*

ijC untuk seluruh 0* ijT

dimana cij*

adalah biaya minimum dari i ke j. Tpij * adalah arus

pada lintasan yang memenuhi prinsip Wardrop pertama dan semua

biaya dihitung setelah Tpij* dibebani. Dalam hal ini arus pada

lintasan a dihasilkan dari rumusan berikut :

pij

pij

a

pija TV (4)

Dimana : 1 jika ruas a berada pada lintasan p dari i ke j

a

pij =

*

ijC untuk seluruh 0* ijT

PerTran 6 - 10

Dan biaya sepanjang lintasan dapat dihitung sebagai berikut:

a

aa

a

pijpij VCC )(.*

Dimana *

aV dihitung berdasarkan persamaan (4)

Beckmann (1956) mengajukan rumusan matematis user equilibrium,

beliau telah merumuskan kondisi equilibrium sebagai equivalent

convex programming problem dan telah terbukti bahwa terdapat

solusi yang unique, dalam program matematis, rumusannya

dinyatakan sebagai berikut:

Min

Batasan : 0pijT dan ijpij

pij TT Dimana :

Tij = permintaan perjalanan dari asal i ke tujuan j

Tpij = arus dari asal i ke tujuan j yang menggunakan lintasan

pij

a

V

apij

a

dvvCTZ0

).(}{

PerTran 6 - 11

Turunan fungsi objektif z terhadap Tpij diuraikan sebagi berikut :

Tetapi persamaan (4)

a

pij

pij

a

T

V

Karena Va hanya tergantung pada Tpij bila lintasan (pij) melalui ruas a,

Oleh karena itu :

a

V

a

pijpij

a

dvvCTT

Z

0).(

pij

a

a

V

a

a TdvvC

dV

d a

.).(0

aa

V

a

a

VCdvvCdV

d a.).(

0

pij

a

pija

a

a

pij

cVCT

Z

).(

PerTran 6 - 12

Turunan kedua dari fungsi objektif z terhadap Tpij adalah :

(5)

Persamaan (5) ini mempunyai nilai lebih besar atau sama dengan nol

hanya jika fungsi turunan hubungan antara biayaarus bernilai

positif atau nol (non-decreasing functions).

Turunan kedua, persamaan (5), menunjukkan bahwa fungsi objektif

z adalah fungsi konvex terhadap Tpij . Sedangkan turunan

pertama, menunjukkan bahwa kelandaian (slope) di setiap titik pada

suatu permukaan yang berkenaan dengan Tpij sama dengan biaya

sepanjang lintasan tertentu pij.

a

pija

a

a

pijpij

VCTT

Z).(

2

2

a

pij

a pij

a

a

aa

T

V

dV

VdC

.

)(.

).(

a

pij

a

a

pij

a

aa

dV

VdC ..

).(

PerTran 6 - 13

Min (6)

Fungsi ini dapat juga dinyatakan dalam bentuk sebagai berikut :

Min (7)

dimana Cma is ongkos marginal perjalanan sepanjang ruas a yang

diperoleh dari rumusan berikut :

(8)

Persamaan (8) telah diterangkan di depan

Harus dicatat, formulasi user equilibrium dan system optimal yang

dikemukakan oleh Beckmann (1956) diatas memberikan batasan

bahwa ca adalah fungsi dari Va saja atau separable. Asumsi

tersebut mungkin tidak merepresentasikan situasi sebenarnya

a

aapij vCVTZ ).(.}{

a

V

mapij

a

dvvCTZ0

).(}{

a

aaaaa

a

aaama

v

vcvvc

v

vcvC

).(.

).(.( .

PerTran 6 - 14

pada jaringan jalan dalam kota dimana biaya pada ruas a merupakan

interaksi antara fungsi arus di arus a dengan ruas lainnya (Non-

separable). Dafermos (1971) mengusulkan perlunya fungsi biaya

non-separable untuk memodelkan fenomena ini.

Dengan merepresentasikan fungsi objektif z sebagai integral garis,

beliau mengusulkan formulasi masalah minimisasi fungsi tersebut

sebagai berikut:

Min (9)

Dimana menunjukkan integral garis dan v adalah vektor

dari arus pada seluruh ruan , dengan batasan :

pij

ijpij TT (10)

0pijT (11)

(12)

Model Dafermos tersebut mengasumsikan bahwa adalah

fungsi dari vektor arus pada seluruh ruas dan matriks Jacobian (J)

a

v

a

a

T

pij

ij

uduCuduCpij

00).().(

pij

pij

a

pija TV .

)(Vcc aa

PerTran 6 - 15

dari fungsi biaya (ca/Vb) adalah simetris dan bernilai positif.

Tetapi pendekatan di atas tidak dapat digunakan jika matriks

Jacobian (J) dari fungsi biaya (ca/Vb) tidak simetris

(asymmetric cost function). Pendekatan yang lazim digunakan untuk

menyelesaikan permasalahan ini adalah metode diagonalisasi

(diagonalisati

WARDROP EQUILIBRIUM

Prinsip equilibrium merupakan prinsip keseimbangan dalam

pemilihan rute dengan mengacu pada aspek biaya minimal.

C1(V1) C2(V2)

C2 C1

V1* = Volume 1 optimum

V2* = Volume 2 optimum

Z

V1 (V1*,V2*) V2

Luas daerah arsiran (Z) merupakan luasan minimal (Min Z)

yang harus diupayakan agar diperoleh biaya perjalanan minimal

PerTran 6 - 16

1. USER EQUILIBRIUM (UE)

Prinsip ini menyatakan :

Pada suatu kondisi equilibrium, lalu lintas akan merekayasa

dirinya sendiri pada jaringan jalan yang macet sehingga tidak

ada pengendara yang dapat mengurangi biaya perjalanannya

dengan merubah rute atau Waktu tempuh disemua rute-rute

yang dilalui atau dipilih adalah sama, dan lebih singkat dari

yang mungkin dialami seorang pengendara melalui rute yang

tidak terpilih

2. SISTEM OPTIMUM (SO)

Total biaya perjalanan minimum

Beda antara UE dan SO

Pada UE berorintasi pada rute atau biaya perjalanan rute

sedang pada SO berorientasi pada total biaya perjalanan

minimal dari suatu jaringan. Artinya pada suatu keseimbangan

jaringan, kebijakan yang diterapkan pada suatu rute tertentu,

PerTran 6 - 17

missal Road charging, belum tentu akan meminimalkan total

jaringan.

6.5. NOTASI DAN SIMBOL

1. NOTASI

Tij = Total perjalanan dari i ke j

Pij = Suatu rute (path) dari i ke j

Tpij = Jumlah perjalanan dari i ke j di pij

Va = Arus pada ruas jalan a

Ca(V) = Fungsi biaya arus diruas jalan a

Cpij = Biaya sepanjang rute (path) pij

Ca = Biaya diruas jalan a

2. Formulasi UE

Min Z = a

Va

0

dv)V(Ca

Dengan batasan :

Tpij 0

Tij

pij

Tpij

PerTran 6 - 18

3. Formulasi SO

Min Z =

Dengan batasan :

Tpij 0

Tij

pij

Tpij

4. Contoh Soal

2

V

0 1

t1 t2

V1 V2

V1* V2*

a

VCaVa )(.

PerTran 6 - 19

C1 = 5+3V1

C2 = 10+2V2

Tod = V1+V2=100 V2 = 100-V1

UE (Ongkos disemua rute yang dilalui adalah sama)

C1 = C2

5+3V1 = 10+2V2

5+3V1 = 10+2(100-V1)

5+3V1 = 10+200-2V1

-205+5V1 = 0

V1 = 41 & C1 = 128 biaya sama tapi

V2 = 59 & C2 = 128 volume arus beda

Biaya Total system : C = C1(V1).V1 + C2(V2).V2

= 128 x 41 + 128 x 59

= 12.800

PerTran 6 - 20

SO (Total biaya perjalanan minimum)

C(V1,V2) minimum

C =

n

1i

)Vi(Ci.Vi

= (5+3V1).V1 + (10+2V2).V2

= 5V1+3V1+10V2+2V2

= 5V1+3V1+10(100-V1)+2(100-V1)

= 5V1+3V1+1000-10V1+2(10.000-200V1+V1)

= 5V1- 405V1 + 21000

Cmin V

C

= 0 10V1-405 = 0

V1 = 40,5

V2 = 59,5

Cmin = (5+3.40,5)+(10+2.59,5) = 12.798,75

PerTran 6 - 21

C1 C2

SO C1

C2

UE t2

t1 10

5

(V1*,V2*)

V1 V2

(V1SO ,V2SO )

Agar UE bergeser SO maka :

Kedua jalan dipajak

Jalan 1 fungsi biaya arus bertambah sebesar t1

Jalan 2 fungsi biaya arus bertambah sebesar t2

PerTran 6 - 22

SOAL 1 C1 = 1+3V1

C2 = 2+V2

Diketahui O 2 D C3 = 3+2V2

3 Tod = 44

Diminta :

1. Arus dengan UE dan SO

2. Tunjukkan bahwa jawaban 1 dapat diperoleh dengan

Algoritma Frank Wolfe

Jawaban

1.a. USER EQUILIBRIUM

Prinsip C1=C2=C3=seluruh biaya disetiap ruas sama

Total V=V1+V2+V3=Tod=44 V1=44-V2-V3

C1=C2

1+3V1=2+V2

1+3(44-V2-V3)=2+V2

131-4V2-3V3=0(1)

C1=C3

1+3V1=3+2V3

1+3(44-V2-V3)=3+2V3

130-3V2-5V3=0(2)

Jika (1) dikalikan 3 dan (2) dikalikan 4 maka

393-12V2-9V3 =0....................(1)

520-12V2-20V3 =0....................(2)

-127+11V3 =0

PerTran 6 - 23

V3 =11,545

131-4V2-3(11,545) =0....................(1)

V2 =24,091

V1= 44-V2-V3 = 44-24,091-11,545 = 8,364

C1 = 1+3V1 = 1+3.8,364 = 26,091

C2 = 2+V2 = 2+24,091 = 26,091

C3 = 3+2V2 = 3+2.11,545= 26,090

C = C1.V1+C2.V2+C3.V3

= (26,091.8,364)+(26,091.24,091)+(26,090.11,545)

= 1147,992

b. SISTEM OPTIMUM

C (V1,V2,V3)

C =

n

1i

)Vi(Ci.Vi

C1V1 = (44-V2-V3) (1+3(44-V2-V3))

= (44-V2-V3) (133-3V2-3V3)

= 5852-132V2-132V3-133V2+3V2+3V2.V3-133V3

+3V2.V3+3V3

C2V2 = (2+V2).V2 = 2V2+V2

C3V3 = (3+2V3).V3 = 3V3+2V3

C = C1.V1+C2.V2+C3.V3

5852-256V2-256V3+6V2.V3+3V2+3V3+2V2

+V2+3V3+2V3

= 5852-263V2-262V3+6V2.V3+4V2+5V3

PerTran 6 - 24

2V

C

= -263+6V3+8V2 = 0 (1)........X3

3V

C

= -262+6V2+10V3 = 0 .(2)........X4

-789+24V2+18V3 = 0.............(1)

-1048+24V2+40V3 = 0.............(2)

259+0 -22V3 = 0

V3 = 11,773

-263+6V3+8V2 = 0 (1)

-263+6(11,773)+8V2 = 0

V2 = 24,0433

V1 = 44-V2-V3 = 44-24,0453-11,773 = 8,1818

C1 = 1+3V1 = 1+3.8,1818 = 25,545

C2 = 2+V2 = 2+24,0453 = 26,0453

C3 = 3+2V2 = 3+2.11,773 = 26,546

C = C1.V1+C2.V2+C3.V3

= (25,545.8,1818)+(26,0453.24,0453)+(26,546.11,773)

= 1147,7972