3. Kinematika Dasar
-
Upload
baithqi-putraka-d -
Category
Documents
-
view
75 -
download
9
description
Transcript of 3. Kinematika Dasar

KINEMATIKA
Tim Fisika FTP

PENDAHULUANMekanika : ilmu yang menggambarkan dan meramalkan kondisi benda yang diam atau bergerak karena pengaruh gaya yang beraksi pada benda.
Tujuan mekanika :• Menerangkan dan meramalkan gejala fisi
sehingga dapat melakukan dasar-dasar bagi aplikasi teknis landasan berbagai masalah teknik
• Membuat dan memecahkan model matematis yang menggambarkan pengaruh dan gerakan pada struktur dan mesin

MEKANIKA
Kinematika : deskripsi benda bergerak Mekanika benda tegar :
a) statika : ilmu yang menyangkut benda dalam keadaan diam (tegar sempurna)
b) dinamika : ilmu yang menyangkut benda dalam keadaan bergerak (tegar sempurna)
Mekanika benda berubah bentuk (mechanics of deformable bodies)
Mekanika fluida : ilmu yang menyangkut pergerakan fluida, baik fluida yang termampatkan (compressible fluids) dan termampatkan (incompressible fluids)

4
Cabang mekanika teknik
• Statika: studi/analisis tentang gaya dan keseimbangan benda tegar (rigid body) yang dikenai gaya.
• Dinamika: studi/analisis gerakan benda dan hubungannya dengan gaya yang menyebabkan gerakan.
• Kinematika: studi/analisis tentang ruang dan waktu dari gerak suatu benda
• Kinetika: studi/analisis tentang hukum gerak dari suatu benda yang akibat adanya gaya atau studi/analisis tentang hubungan antara gaya dan gerak akibat gaya tersebut.
Benda: Benda tegar (rigid
body), atom/partikel Fluida

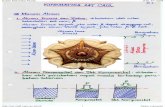
GERAK PADA SATU DIMENSI

GERAK
Tranlasi : suatu gerakan dimana setiap garis pada benda tetap sejajar terhadap kedudukan awalnya pada setiap saat.
Rotasi : semua partikel bergerak pada lintasan melingkar terhadap sumbu rotasi.

PERPINDAHAN (DISPLACEMENT) perubahan posisi benda tersebut Seberapa jauh jarak benda tersebut dari
titik awalnya Besaran yang memiliki besar dan arah
vektor

JARAK (DISTANCE TRAVELED)? total jarak yang ditempuh sebuah
obyek dari titik awal ke titik akhir
West East
Y
X
50 m 100 m
Displacement = 50 m
Distance Traveled = 150 m

LAJU RATA-RATA
Laju : seberapa jauh sebuah benda berjalan dalam suatu selang waktu tertentu.
Laju rata-rata : jarak yang ditempuh sepanjang lintasannya dibagi waktu yang diperlukan untuk menempuh jarak tersebut
diperlukanyangtempuhwaktu
tempuhjarakrataratalaju

KECEPATAN RATA-RATA
Kecepatan : nilai seberapa cepat sebuah benda bergerak maupun arah geraknya vektor
diperlukanyangtempuhwaktu
nperpindaharatarata.kec
t
x
tt
xxv
12
12

CONTOH :
Seseorang berjalan 70 m ke arah timur dan 30 m ke barat. Misalkan perjalanan ini memerlukana waktu 70 s. Berapakah laju rata-rata dan kecepatan rata-ratanya ? Jawaban :Laju rata-rata : 1,4 m/sKec. rata-rata : 0,57 m/s
Catatan :Ketidaksamaan antara laju dan besar kecepatan terjadi pada beberapa kasus, tetapi hanya untuk nilai rata-rata dan kita jarang memperhitungkannya

CONTOH :
Posisi seorang pelarisebagai fungsi waktu digambarkan sepanjang sumbu x dari suatu sistem koordinat. Selama selang waktu 3 s, posisi pelari berubah dari x1 = 50 m menjadi x2 = 30,5 m. Berapa kecepatan rata-rata pelari tersebut ?Jawaban :

PERCEPATAN
Benda yang kecepatannya berubah dikatakan mengalami percepatan
Percepatan : seberapa cepat kecepatan sebuah benda berubah.
diperlukanyangwaktu
tankecepaperubahanrataratatanpercepa
t
v
tt
vva
12
12

Gambar a : gerak dengan kecepatan konstan Gambar b : gerak dengan percepatan positif
(+) atau dipercepat Gambar c : gerak dengan percepatan negatif
(-) atau perlambatan

CONTOH
1. Sebuah mobil mengalami percepatan sepanjang jalan yang lurus dari keadaan diam sampai kecepatan 75 km/jam dalam waktu 5 s, berapa besar percepatan rata-ratanya ?
2. Sebuah mobil bergerak ke kanan sepanjang jalan bebas hambatan yang lurus, yang kita anggap sebagai sumbu x positif dan si pengemudi menginjak rem. Jika kecepatan awal adalah v1 = 15 m/s dan diperlukana waktu 5 s untuk memperlambat kecepatan sampai v2 = 5 m/s, berapa percepatan rata-rata mobil tersebut?

GERAK DENGAN PERCEPATAN KONSTAN
2
vvv 0
t
vva 0 0vvat atvv 0
vtxx 0 t2
vvxx 00
200 at
2
1tvxx
0xxS 20 at
2
1tvS
vtS
dimana

t2
vvxvtxx 000
a
vvtanadim 0
a2
vvx
2
vv
2
vvxx
20
2
000
0
020
2 xxa2vv aS2vv 20
2

CONTOH SOAL :
Anda sedang merancang sebuah bandara untuk pesawat-pesawat kecil. Satu jenis pesawat yang mungkin menggunakan bandara ini harus mencapai laju setidak-tidaknya sebesar 27,8 m/s sebelum lepas landas dan dapat mengalami percepatan 2 m/s2. (a) jika panjang pacu 150 m, dapatkah pesawat ini
mencapai laju yang dibutuhkan untuk lepas landas? (b) jika tidak, berapa seharusnya panjang minimum
landasan pacu tersebut?

CONTOH SOALSebuah mobil melaju pada kecepatan konstan 45 m /s melewati seorang polisi dengan sepeda motornya tersembunyi di balik papan iklan. Satu detik setelah mobil tersebut melaju melewati papan iklan, polisi keluar untuk menangkap mobil tersebut dengan percepatan 3m/s2. Berapa lama waktu yang diperlukan polisi tersebut untuk menyalip mobil?

JAWAB Jarak mobil ketika polisi mulai mengejar:
Smobil = vmobil.t = 45m/s x 1 s = 45 m
Jarak yang telah ditempuh oleh motor polisi ketika berhasil menangkap mobil adalah:S= V0t + ½ at2 = 0 + ½ 3t2
Jarak yang telah ditempuh polisi waktu berhasil mengejar mobil adalah sama dengan jarak mobil, sehingga:S polisi= S mobil½ at2 = 45 + vmobil.t
½ .3.t2 = 45 + 45t 1.5 t2 – 45 t – 45 = 0

GERAK JATUH BEBAS
Pada dasarnya gerak jatuh bebas sama dengan gerak dengan percepatan.
Hipotesa Galileo : jatuh bebas mengalami percepatan konstan g
Percepatan menggunakan percepatan gravitasi, yaitu +9.8 m/s2
Untuk gerak vertikal ke atas, percepatan juga menggunakan percepatan gravitasi, hanya saja nilainya negatif (-)

CONTOH SOAL
Misalkan sebuah bola dijatuhkan dari sebuah menara dengan ketinggian 70 m. Seberapa jauh bola itu jatuh setelah 1 s, 2 s dan 3 s? Anggap y positif ke bawah. Abaikan hambatan udara

CONTOH SOAL
Sebuah batu dilempar vertikal ke atas dari atap suatu gedung dengan kecepatan awal 20m/s. Tinggi gedung tersebut adalah 50 m. Hitunglah:a. Tinggi maksimal batu tersebut
diukur dari permukaan tanahb. Berapa lama batu tersebut akan
menyentuh tanah, dihitung dari saat ketika batu tersebut dilempar.
c. Berapa kecepatan batu saat menyentuh tanah

JAWAB
Waktu untuk mencapai titik tertinggivt=vo + at 0 = vo + at t= -20/(-9.8)= 2.04 detik
Ketinggian maksimal batuStotal = SB + 50 m = 50 + v0t + ½ at2
= 50 + (20).(2.04)+ ½ (-9.8).(2.04)2= 70.4 m Kecepatan saat batu menyentuh tanah
vt2=vo
2+2as = 0 + 2(9.8).(70.4) = 37.15 m/s

GERAK 2 DIMENSI

GERAK PARABOLA
Gerak parabola mempunyai 2 komponen gerak, yaitu gerak lurus ke arah horisontal (sumbu x) dan gerak vertikal/ jatuh bebas (sumbu y)

GERAK PARABOLA Persamaan pada sumbu x :
vx = vo cos
x = vo cos . t Persamaan pada sumbu y :
vy = vo sin - g . t
y = vo sin . t – ½.g . t2 Untuk sembarang titik P pada lintasan :
x
yyxp v
vtgvvv ;22

GERAK PARABOLA
Syarat benda mencapai titik tertinggi adalah vy = 0
g
vx
g
vy
g
vt
2sin
2
sin
sin2
20
max
220
max
0max

PERSAMAAN-PERSAMAAN UMUM GERAK KINEMATIKA UNTUK PERCEPATAN KONSTAN DALAM DUA DIMENSI
x komponen horisontal
0x20x
2x
2x0x0
x0xx
xxa2vv
ta2
1tvxx
tavv
y komponen vertikal
0y20y
2y
2y0y0
y0yy
yya2vv
ta2
1tvyy
tavv

PERSAMAAN-PERSAMAAN GERAK KINEMATIKA UNTUK GERAK PELURU (Y POSITIF ARAH KE ATAS; AX = 0, AY = - G = - 9,8 M/S2)
Gerak horisontal(ax = 0, vx = konstan)
tvxx
vv
0x0
0xx
Gerak vertikal(ay = - g = konstan)
gy2vv
gt2
1tvyy
gtvv
20y
2y
20y0
0yy

LATIHAN DI RUMAH
Suatu peluru ditembakkan dengan kecepatan awal vo = 100 m/det dengan sudut elevasi dan percepatan grafitasi g = 10 m/s2. Jika ditentukan cos = 0,6 maka tentukan :
Kedudukan peluru setelah 5 detik. Hitung kecepatan peluru pada saat 5 detik
tersebut. Hitung Ketinggian maksimal peluru Hitung jauh tembakan pada arah mendatar.

KECEPATAN RELATIF
Kecepatan sebuah benda relatif terhadap satu kerangka acuan bisa didapatkan dengan penambahan vektor jika kecepatannya relatif terhadap kerangka acuan kedua, dan kecepatan relatif kedua kerangka acuan diketahui
ATPAPT vvv

CONTOH SOAL
Perahu yang sama (vPA = 1,85 m/s) sekarang menuju langsung ke seberang sungai yang arusnya tetap 1,2 m/s.(a) Berapa keceppatan (besar dan arah) perahu relatif
terhadap tepi sungai ?(b) Jika sungai tersebut lebarnya 110 m, berapa lama
waktu yang diperlukan perahu untuk menyeberang dan berapa jauh ke hilir perahu tersebut pada waktu itu?

GERAK MELINGKAR BERATURAN
Sebuah benda yang bergerak membentuk suatu lingkaran dengan laju konstan v.
Besar kecepatan konstan Arah kecepatan terus
berubah sementara benda bergerak dalam lingkarant
v
t
vva 12

v menuju ke arah pusat lingkaran
a mempunyai arah yang sama dengan v, a juga harus menunjuk ke arah pusat lingkaran.
Percepatan sentripetal (percepatan yang mencari pusat) atau percepatan radial (mempunyai arah sepanjang radius menuju pusat lingkaran) aR
r
l
v
v

PERCEPATAN SENTRIPETAL
r
l
v
v
l
r
vv
t
l
r
v
t
vaR
Karena l/t adalah laju linier v, maka
r
va
2
R

FREKUENSI DAN PERIODE
Gerak melingkar sering dideskripsikan dalam frekuensi f sebagai jumlah putaran per sekon.
Periode T : waktu yang diperlukan untuk menyelesaikan satu putaran
fT
1
T
rv
2

CONTOH SOAL
1) Sebuah bola 150 g diujung sebuah tali diputar secara beraturan membentuk lingkaran horisontal dengan radius 0,6 m. Bola membuat 2 putaran dalam satu sekon. Berapa percepatan sentripetalnya?
2) Orbit bulan di sekeliling bumi yang hampir bulat mempunyai radius sekitar 384.000 km dan periode T selana 27,3 hari. Tentukan percepatan Bulan terhadap Bumi